Эвольвентная зубчатая передача.

Элементы эвольвентной зубчатой пере­дачи. На рис. 15.2 показана зубчатая передача внешнего зацепле­ния _w (угол зацепления), полюс зацепления P, межосевое расстояние а_w, начальные окружности радиусами r_w1 и r_w2. Эти элементы были рассмотрены ранее (в лекции 13) при знакомстве со свойствами эвольвентного зацеп­ления.

В

Рис 15.2

точках В^’ и B^’’ линия зацепления пересекается окружностями вершин зубьев колес; в точке В^’ сопряженные профили входят в зацепление, а в точке B^’’ - выходят из зацепления. Процесс взаимодействия главных поверхностей сопряженных зубьев проис­ходит на участке В^’B^’’ линии зацепления; эта часть линии зацеп­ления называется активной линией зацепления. Зубчатая передача должна быть спроектирована так, чтобы участок В^’B^’’ укладывался в пределах линии зацепления N₁N₂. Если точки В^’ и B^’’ выйдут за эти пределы, то в зубчатой передаче произойдет заклинивание.

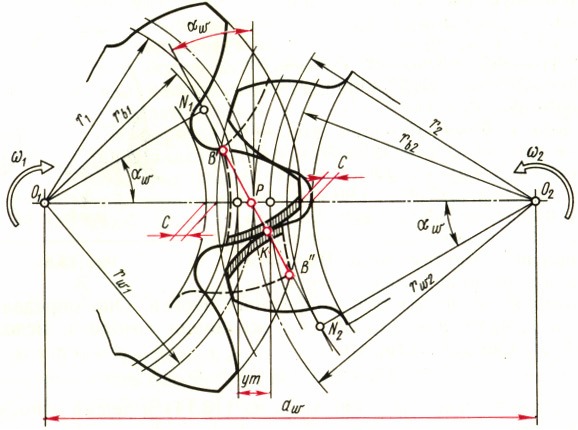
Рис. 15.2

При заданном направлении вращения только одна сторона зуба будет передавать и воспринимать усилие; ее называют рабочей стороной (профилем) зуба. В зацеплении участвуют активные профили зубьев, расположенные на рабочих сторонах зубьев, которые соответствуют активной линии зацепления. На рис. 15.2 активные профили за­штрихованы.

Между окружностью вершин одного колеса и окружностью впа­дин другого имеется расстояние, которое называется радиальным зазором. На рис. 15.2 радиальный зазор отмечен буквой С его ве­личина выражается произведением коэффициента с^* на модуль, т.е С = с^*m, где с^* = 0,25.

Уравнения эвольвентной зубчатой передачи.

При составлении уравнений для определения угла зацепления _w и межосевого рас­стояния a_w следует иметь в виду, что номинальные значения этих величин подсчитывают при условии, что зубья одного колеса входят во впадины другого плотно, без бокового зазора. Учтя это, а также то, что начальные окружности катятся друг по другу без сколь­жения, запишем s_w1 = e_w2 и s_w2 = e_w1, где s_w1 и s_w2 - толщина зубьев, а e_w1 и e_w2 - ширина впадин по начальным окружностям колес зубчатой передачи.

Поскольку начальные окружности перекатываются без сколь­жения, то шаги p_w1 и p_w2 пo этим окружностям равны друг другу: p_w1 = p_w2 = p_w.

Шаг p_w = s_w1 + e_w1, или, поскольку s_w2 = e_w1 :

p_w = s_w1 + s_w2 (15.6)

С другой стороны, шаг по начальной окружности :

Учитывая уравнения (14.2), (14.3) и (14.6), выразим толщину зубьев s_w1 и s_w2 по формуле (14.6) и подставим в (15.6). Проделав несложные преобразования, получим уравнение для определения угла зацепления :

inv _w = inv + 2x tg /z (15.7)

где x = x₁ + x₂, z = z₁ + z₂. После подсчета инволюты угла за­цепления по уравнению (15.7) сам угол _w следует определить по таблице инволютной функции.

Межосевое расстояние зубчатой передачи:

а_w = r_w1 + r_w2

Учитывая зависимость (14.6), можно записать:

поэтому межосевое расстояние

(15.8)

Межосевое расстояние может быть выражено также следую­щим образом (рис. 15.2):

а_w = r₁ + r₂ +ym (15.9)

где ym - расстояние между делительными окружностями. Оно на­зывается воспринимаемым смещением, а величина у - коэффициен­том воспринимаемого смещения.

Приравнивая (15.8) и (15.9) и учитывая (14.3), получим фор­мулу для определения коэффициента воспринимаемого смещения:

(15.10)

При расчете косозубых передач применяют те же формулы, что и при расчете прямозубых, но вместо параметров m и берут m/cos и _t а произведения x tg и уm сохраняют без изменения.

Определим уравнительное смещение зубчатой передачи. При геометрическом проектировании передачи должны бить выполнены два условия: 1) зубья колес должны зацепляться друг с другом теоретически без бокового зазора; 2) между окружностями вершин и впадин зубчатых колес должен быть стандартный радиальный зазор c = c^*m = 0,25m.

Выполнение первого условия обеспечивается тем, что межосе­вое расстояние выражается через воспринимаемое смещение по формуле (15.9). Второе условие требует, чтобы:

a_w = r_a1 + с*m + r_f2 (15.11)

Совместное решение уравнений (15.9) и (15.11) дает:

r₁ + ym + r₂ = r_a1 + C + r_f2

или

r₁ + ym + r₂ = r_a1 + C + r_a2 - h

Подставляя в это равенство формулы для r_a1, r_a1 и h из лекции 14 после преобразования придем к выражению:

ym = x₁m - ym + x₂m

откуда получим у - коэффициент уравнительного смещения, упо­мянутый ранее

у = x - y (15.12)

Итак, уравнительное смещение ym (cм. схему станочного зацепления) вводится для получения зубчатой передачи без бокового зазора и со стан­дартной величиной радиального зазора.

Если зубчатая передача составлена из колес без смещений (x₁ = 0, x₂ = 0, x = 0, x = x₁ + x₂ = 0), то, согласно уравнениям (15.7), (15.10), (15.12) и (15.9) такая передача будет характеризоваться следующими параметрами: угол зацепления _w = = 20°, коэф­фициент воспринимаемого смещения y = 0, коэффициент уравни­тельного смещении y = 0, межосевое расстояние a_w = r₁ + r₂ = m(z₁ + z₂)/2, т.е. равно сумме радиусов делительных окружно­стей. При указанных условиях радиусы начальных окружностей r_w1 = mz₁/2 = r₁, r_w2 = mz₂/2 = r₂ т.е. начальные окружности колес совпадают с их делительными окружностями.

О

Рис. 15.3

собенности эвольвентной передачи внутреннего зацепления. На рис. 15.3 изображена передача внутреннего зацепления. Мень­шее колесо (шестерня), обозначенное номером 1, имеет внешние зубья; большее колесо, именуемое просто колесом и обозначенное номером 2. имеет внутренние зубья. Инструментом для изготовле­ния колес с внутренними зубьями способом сгибания является не реечный инструмент, а долбяк (инструментальное колесо), число зубьев и основные размеры которого стандартизованы. При изго­товлении колес

долбяком может произойти не только подрезание и заострение зубьев, но и срезание их у вершины. Предотвращение этого явления должно быть учтено при проектировании передачи внутреннего зацепления.

П

Рис. 15.3

ри внутреннем зацеплении, в отличии от внешнего, эвольвентные профили Э₁ и Э₂ пересекаются на участке N₁N₂. Кроме того, при внутреннем зацеплении может иметь место еще один вид пересечения эвольвент, если числа зубьев шес­терни (z₁) и колеса (z₂) близки друг к другу.

В правильно спроектированной передаче внутреннего зацепле­ния должны отсутствовать оба вида пересечения эвольвентных про­филей. Это значит, что активная часть линии внутреннего зацеп­ления должна целиком находиться вне отрезка N₁N₂. Кроме того, числа зубьев z₁ и z₂ должны подчиняться определенным ограниче­ниям.

Для передачи, составленной из колес без смещений, нарезаемых стандартным долбяком, необходимо иметь z₁ 20, z₂ 85, а раз­ность z₁ - z₂ 8. Если передачу составить из колес со смещениями. то z'i и 22—2i можно существенно уменьшить и сократить тем са­мым размеры всей передачи.