МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ

УНИВЕРСИТЕТ»

Реферат по математике на тему:

«Числовые ряды»

Выполнила:

студент 1 курса

1 группы очного отделения

физико- математического факультета

(технология)

Крюков Роман Сергеевич

Преподаватель:

Овсянникова Алла Николаевна

Воронеж 2014

Оглавление

1. ЧИСЛОВОЙ РЯД И ЕГО СВОЙСТВА…………………………………..….3

1.1 Понятие числового ряда………………………………………………….…3

2.СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ ЧИСЛОВЫХ РЯДОВ…………..…4

2.1 Признаки сходимости числовых рядов с положительными членами…....4

3.ЗНАКОЧЕРЕДУЮЩИЕСЯ РЯДЫ. ПРИЗНАК ЛЕЙБНИЦА……………...5

3.1 Понятие знакочередующегося ряда………………………………………..5

3.2 Признак Лейбница…………………………………………………………..6

4.АБСОЛЮТНАЯ И УСЛОВНАЯ СХОДИМОСТЬ ЗНАКОПЕРЕМЕННЫХ РЯДОВ…………………………………………………………………………..7

4.1 Абсолютная и условная сходимость………………………………………7

4.2 Свойства абсолютно сходящихся и условно сходящихся рядов………..8

5.ФУНКЦИОНАЛЬНЫЕ РЯДЫ………………………………………………8

5.1Основные понятия…………………………………………………………..8

5.2Функциональный ряд, его сходимость…………………………………….9

6.СТЕПЕННЫЕ РЯДЫ………………………………………………………..10

7.РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ…………………….11

8.Приложение рядов к приближенным вычислениям…….12

8.1. Вычисление значений функций с помощью рядов……………………..13

9.РЯДЫ ФУРЬЕ………………………………………………………………..13

9.1. Понятие ряда Фурье………………………………………………………13

9.2. Определение коэффициентов ряда по формулам Фурье……………….14

9.3 Оценка коэффициентов Фурье……………………………………………15

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ…………………………..20

1. Числовой ряд и его свойства

1.1 Понятие числового ряда

ОПРЕДЕЛЕНИЕ. Пара числовых последовательностей { a_n } и { S_n } , где 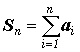  называется (числовым) рядом (или бесконечной суммой) и обозначается  . Элементы последовательности { a_n } называют членами ряда, а элементы последовательности { S_n } – частичными суммами ряда.

ОПРЕДЕЛЕНИЕ. Если существует конечный предел последовательности { S_n } , который мы обозначим S, тогда S называют суммой ряда; а сам ряд именуют сходящимся и пишут : 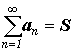 . Если же последовательность { S_n } не имеет конечного предела, ряд именуют расходящимся.

Для задания ряда достаточно задать только одну из последовательностей { a_n } или { S_n }. Сходимость ряда эквивалентна сходимости последовательности { S_n } , и поэтому исследование ряда можно свести к исследованию последовательности { S_n }.

1.2.Свойства сходящихся рядов.

1. Если ряд сходится, тогда последовательность членов ряда { a_n } имеет предел равный нулю. (Свойство следует из Критерия Коши для сходимости последовательности { S_n }. )

2. (Сходимость линейной комбинации) Если два ряда сходятся, то сходится и их линейная комбинация, причем :

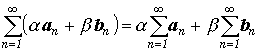
(Свойство следует из свойства сходимости линейной комбинации последовательностей, примененного к последовательностям частичных сумм.)

3. Для ряда   назовем k-ым остатком ряда ряд вида 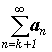 . Если ряд сходится, тогда сходится и любой его остаток. Если сходится какой-то из остатков, тогда сходится и весь ряд, причем если обозначить R_n сумму n-го остатка ряда, тогда при любых значениях n выполнено равенство :

S = S_n + R_n

4. Из предыдущего свойства следует, что остатки сходящегося ряда стремятся к нулю.

2.Сходимость положительных числовых рядов

2.1 Признаки сходимости числовых рядов с положительными членами

Признак Даламбера. Пусть дан числовой ряд

                                             

с положительными членами   и пусть существует предел

                                ρ =  .

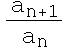Тогда при ρ < 1 ряд сходится, а при ρ > 1 ряд расходится.

Можно указать как сходящиеся, так и расходящиеся ряды, для которых ρ = 1.

Признак Коши. Пусть для числового ряда ( 1 ) с положительными членами существует предел

                                        σ =   

Тогда при σ < 1 ряд сходится, а при σ > 1 ряд расходится.

Можно указать как сходящиеся, так и расходящиеся ряды, для которых σ = 1.

Интегральный признак Маклорена-Коши. Пусть члены ряда (1) являются значениями некоторой функции  f[x] вещественного аргумента x, которые она принимает при натуральных значениях аргумента

                                  = f [n].

Пусть функция f[x] при x≥1 непрерывна, положительна и монотонно убывает при x→ +∞, тогда ряд (1) сходится или расходится в зависимости от того, существует или нет несобственный интеграл

                              f[x]dx

Теорема сравнения. Пусть даны два положительных ряда

                        (*)      и                 (**)

Если, начиная с некоторого номера N, т.е. при n > N, выполняется неравенство   ≤   , то из сходимости ряда (**) следует сходимость ряда (*), а из расходимости ряда (*) следует расходимость ряда (**).