5.Характеристика передаваемой мощности при сложной связи генератора с приемной системой. Максимальные и предельные нагрузки.

(5)

Полученная выше синусоидальная зависимость активной мощности от угла справедлива для простейшей схемы электропередачи в виде чисто индуктивного сопротивления , которое включает и индуктивное сопротивление генератора.

Теперь мы установим эту зависимость, не накладывая никаких ограничений на характер связи между генератором и приемником, кроме требования постоянства активных , индуктивных и емкостных сопротивлений схемы.

При соблюдении этого условия можно воспользоваться принципом наложения режимов, создаваемых каждой э.д.с. или напряжением, действующим в цепи.

Так, например, для Т-образной схемы замещения передачи (рис.2.7), в на-

ч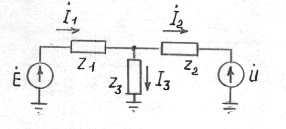 але которой приложена э.д.с. генератора и в конце – напряжение шин бесконечной мощности , режим электропередачи может быть представлен как результат наложения друг на друга двух независимых режимов.

Рис.2.7. Схема замещения электропередачи

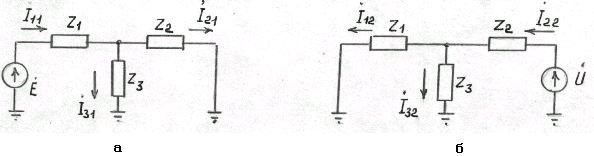В одном из них (рис.2.8, а) токи создаются э.д.с. генератора при напряжении шин приемника , в другом (рис.2.8, б) – напряжением шин приемника (шины бесконечной мощности) при э.д.с. генератора

Рис.2.8. Режимы, создаваемые отдельными источниками

Налагая токи и напряжения этих двух режимов друг на друга, получим токи и напряжения действительного режима работы электропередачи (рис.2.7). При этом, оченвидно, действительный ток генератора

(2.3)

и ток приемной системы (2.4)

Для генератора здесь считаются положительными ток и мощность, отдаваемые в сеть, а для приемной системы – получаемые из сети.

Отдельные составляющие токов генератора и приемной системы пропорциональны соответствующим э.д.с. и напряжению.

Так, например, составляющие и имеют следующие значения:

и

где и - соответственно, собственные сопротивления и проводимости ветвей генератора и приемной системы, которые в данном случае равны:

и

Точно так же и

где и - соответственно, взаимные сопротивления и проводимости ветвей, равные для Т-образной схемы замещения:

Собственные сопротивления ( ) ветвей и собственные их проводимости ( ) определяют абсолютное значение и фазу составляющей тока в данной ветви от действия э.д.с. (напряжения) в данной ветви при отсутствии э.д.с. во всех остальных ветвях.

Взаимные сопротивления ветвей ( ) и взаимные проводимости ветвей определяют абсолютное значение и фазу составляющей тока тока в ветви , от действия э.д.с. (напряжения) в ветви при отсутствии э.д.с. во всех остальных ветвях.

Собственные и взаимные сопротивления (проводимости) определяются исключительно конфигурацией схемы замещения и значениями сопротивлений отдельных ее ветвей. Они могут быть вычислены для схемы замещения любой конфигурации и позволяют получить наиболее общее выражение активной мощности генератора и приемной системы.

Наболее просто собственные и взаимные сопротивления (проводимости) находятся способом единичных токов.

Пусть нужно найти собственную проводимость ветви и взаимную проводимость . Тогда предполагают, что в ветви приложена некая э.д.с. , величина и фаза которой таковы, что в ветви от действия только этой э.д.с. (при равных нулю э.д.с. во всех остальных ветвях) протекает ток . Зная величину тока в ветви , можно найти в этой ветви падение напряжения , далее, производя токораспоределение, находим токи и напряжения во всех ветвях и , в конечном счете, ток и э.д.с. .

При этом взаимная проводимость , а собственная проводимость .

Возвращаясь к нашей задаче (рис.2.7). согласно соотношениям (2.3)-(2.4) токи генератора и приемной системы выражаются следующим образом через собственные и взаимные проводимости ветвей:

Произведение сопряженного вектора тока на вектор напряжения или э.д.с. дает комплексное выражение мощности, действительная часть которого представляет собой значение активной мощности, а мнимая – реактивной мощности.

Мощности генератора и приемной системы соответственно равны:

(2.5)

Отметим, что представляет собой мощность в точке приложения э.д.с. в схеме замещения, то есть внутреннюю мощность генератора за его сопротивлением. Принимая направление вектора за ось отсчета фаз векторов, получаем фазный угол вектора равным нулю и фазный угол вектора равным относительному углу сдвига векторов( и ) , то есть

. (2.6)

В качестве фазных углов собственных и взаимных сопротивлений ветвей входят углы , , ; причем ; .

Углы определяются следующим образом:

; ; .

Поэтому для собственных и взаимных проводимостей ветвей можно записать: ; ; .

Принимая во внимание, что фазные углы сопряженных векторов должны быть взяты со знаком минус, получим для мощностей генератора и приемной системы:

;

или

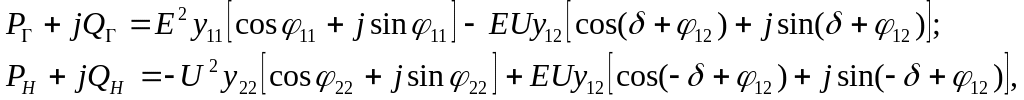(2.7)

откуда

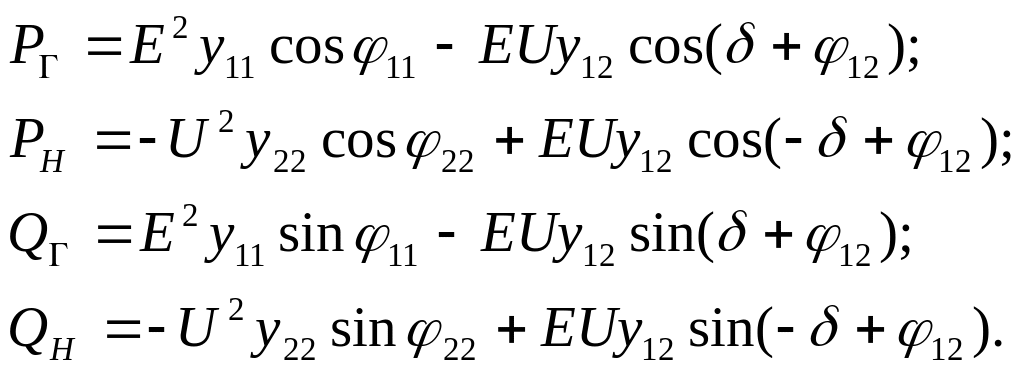(2.8)

Если вместо углов ввести дополняющие их до углы , то выражения (2.8) запишутся в виде:

(2.9)

Структура выражений (2.9) остается одной и той же при любой схеме связи генератора и приемной системы. Вариации конфигурации схемы замещения влияют только на значения собственных и взаимных проводимо-

стей ветвей и углов .

В общем случае при любом числе источников питания в схеме характеристики мощности для -той точки можно представить в следу- ющем виде :

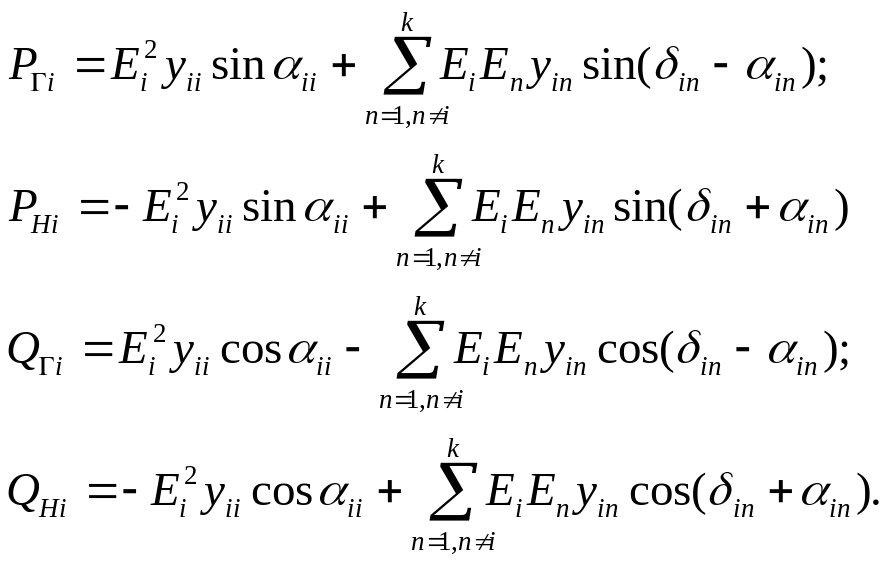(2.10)

Заметим, что выражения (2.10) могут быть получены с учетом следующих соображений:

1.Каждый новый источник питания обусловливает появление дополнительного взаимного тока между ним и рассматриваемой той точки схемы (этим обусловлено появление знака в выражениях 2.10).

2.Замена обозначения на введена для общности записи и является математически корректной, так как э.д.с. и напряжение для той точки схемы имеют одинаковую размерность (В, кВ).

Как видно из (2.10), различие формы записи мощностей для генераторной и нагрузочной той точки схемы состоит лишь только в изменении знаков «+» и «-» в сответствующих выражениях для активной и реактивной мощностей.

Полученные выше выражения позволяют найти максимальные значения параметров режима, то есть те наибольшие значения, которые могут иметь токи и мощности в каком-либо элементе системы.

Так, например, максимальная активная мощность электропередачи, представленной в схеме замещения чисто реактивным сопротивлением , согласно (2.10) будет: , где -модули напряжения (э.д.с.) соответственно в начале и конце сопротивления электропередачи.

Эта мощность будет достигнута при максимально возможноми угле передачи по (2.10) первый член равен нулю для выражения активной мощности, так как и имеют значение, равное нулю( в схеме замещения отсутствуют активные сопротивления).

При представлении той же электропередачи полным сопротивлением максимальная мощность определенная по (2.10) для генераторного конца будет: .

При этом .

Заметим, что не следует путать максимум в значении , обусловленный физическими свойствами передачи энергии переменным током, с факторамит практического порядка, например, температурный режим оборудования, изменения напряжения и т.д.

Ограничения последнего вида называют предельными нагрузками.