28.Порядок расчета режима синхронного генератора при несинхронной частоте его вращения.

Рассмотрим условия работы системы, которая состоит из синхронного генератора, ротор которого вращается с постоянной угловой частотой , отличной от синхронной , и шин неизменного по величине и частоте напряжения.

Принципиальная схема исследуемой системы приведена на рис.9.6, векторная диаграмма – на рис.9.7.

Рис.9.6. Схема простейшей системы

При построении векторной диаграммы предполагается, что при некотором значении , начиная от частота вращения вектора э.д.с изменяется и становится равной , вместо . При этом модуль вектора угол .

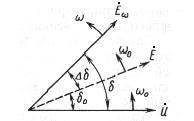
Рис.9.7. Векторная диаграмма системы

Здесь из векторной диаграммы имеем и учитывая, что скольжение , получим .

Таким образом, , (9.1)

если отсчет времени ведется с момента изменения .

При увеличении угловой частоты ротора сверх синхронной и росте угла ( ) скольжение получает отрицательное значение (генераторный режим) (см. рис.9.8).

Рис.9.8. Характер изменений угловой частоты вращения и скольжения

Укажем основные особенности процессов, происходящие при несинхронной работе синхронного генератора:

1. В машине и линии передачи циркулирует ток, имеющий слагающие двух частот и .

2. Синхронная машина одновременно приобретает свойства асинхронной, так как во всех короткозамкнутых обмотках ротора появляются токи, обусловленные наличием скольжения.

3. Появляются изменения параметров режима синхронной машины и параметров других элементов передачи:

а) э.д.с. зависит от скольжения;

б) созданные ею составляющие токов с частотой прооходят через реактивные сопротивления, изменяющиеся для этих токов в отношении и приобретающие новые значения .

Поставленная задача определения статических характеристик мощности при несинхронной работе генератора, сводящаяся к определению токов, мощностей и вращающих моментов, может быть решена тремя способами.

Первый способ основывается на предположении о возможности разделения рассматриваемой машины на две – синхронную и асинхронную, создающие общий вращающий момент .

Синхронная машина, связанная с напряжением , работает с частотой , имеет э.д.с. и развивает вращающий момент . Асинхронная машина присоединена к шинам напряжения , работает со скольжением , развивает вращающий момент и является, в зависимости от знака скольжения, асинхронным двигателем или асинхронным генератором, как это показано на рис.9.9.

Рис.9.9. Разделение несинхронно работающей синхронной машины

на две механически связанные: синхронную и асинхронную

Подчеркнем, что при этом параметры машины , как асинхронной, будут определяться всеми короткозамкнутыми обмотками ее ротора; сопротивление сети в простейшем случае будет введено в цепь статора каждой машины. Это , конечно, возможно только при грубых расчетах первого приближения.

Заметим, что при первом способе можно получить выражения мощностей с помощью схем замещения, пользуясь методом наложения и определяя токи в каждой ветви.

Второй способ нахождения параметров режима (токов, мощностей) при работе с несинхронной частотой сводится к определению дополнительных э.д.с., наводимых в каждой обмотке ротора, и некоторой новой э.д.с. ( или ), действующей в схеме замещения машины.

Третий способ заключается в применении полных уравнений синхронной машины (уравнения Парка-Горева), позволяющих учесть все изменения частоты вращения и обусловленные ими изменения э.д.с. и моментов.

Рассмотрим первый простейший способ определения вращающих моментов согласно схеме, показанной на рис. 9.9. Начнем с синхронного генератора , связанного с шинами . Схема замещения имеет вид, показанный на рис.9.10, где согласно методу наложения

Здесь .

Рис.9.10. Определение токов в несинхронно работающей синхронной машине

методом наложения

Мощности в начале и конце передачи могут быть найдены как

.

При определении э.д.с. предполагается, что появившиеся при независимом возбуждении, возникающие в результате скольжения, дополнительные (наведенные) токи учтены в условной асинхронной машине ; тогда Если ток возбуждения получается от возбудителя и подвозбудителя, сидящих на одном валу с генератором, то . В общем случае можно записать .

С учетом этого найдем . (9.2)

Определим из (9.2) выражение для :

=

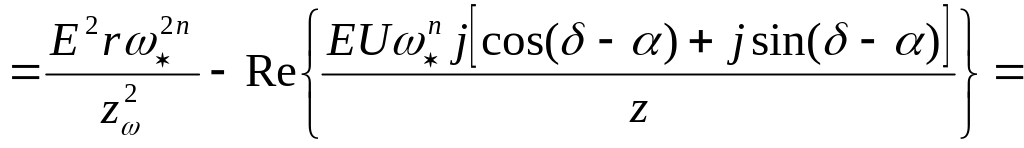
(9.3)

где ; .

Вращающий момент генератора при этом будет

. (9.4)

Здесь первое слагаемое момента , называемое собственным моментом , получается при взаимодействии обмотки ротора, питаемой э.д.с. и обмотки статора, замкнутой на сопротивление . Его зависимость от скольжения при показана на рис. 9.11 (характеристика 1).

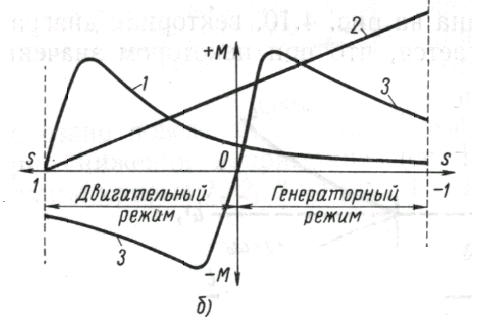
Рис.9.11. Зависимости составляющих момента

несинронно работающей синхронной машины от скольжения при

В простейшем случае при , собственный момент

, (9.4 а)

где .

Заметим, что формула (9.4 а) по своей структуре аналогична известной формуле момента (мощности) асинхронного двигателя.

При член превращается в так называемую собственную мощность .

Второе слагаемое в (9.4) назавается взаимным моментом; при он превращается во взаимную мощность . Зависимость амплитуды взаимного момента от скольжения при дается характеристикой на рис.9.11.

Мнимая часть комплекса , дает реактивную мощность

, (9.5)

где .

В конце передачи значения активной и реактивной мощностей будут

; (9.6)

, (9.7)

где .

Разность активных мощностей в начале и конце передачи при непрерывном изменении положения и величины вектора , оказывается, не равна потерям мощности в активном сопротивлении :

где - дополнительные потери, связанные со скольжением.

Асинхронный момент.

Найдем теперь величину вращающего момента , развиваемого условно выделенной машиной (рис.9.9), которую при отрицательном скольжении считаем генератором, а при положительном – двигателем.

Если предположить, что на роторе генератора имеется только одна обмотка возбуждения, выполненная как равномерно распределенная, то выражение вращающего момента можно записать как:

. (9.8)

Здесь и - параметры схемы замещения асинхронного двигателя, включая внешнее сопротивление .

Для перехода от параметров асинхронного двигателя к параметрам синхронного генератора, воспользуемся комплексной схемой генератора , при- веденной на рис.9.12.

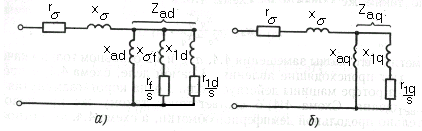
Рис.9.12. Комплексная схема замещения явнополюсной синхронной машины

с учетом демпферной обмотки: а) по продольной оси; б) по поперечной оси

Соответствущие частные схемы для определения реактивных сопротивлений, представляющих генератор в некоторых характерных режимах, приведены в графах (4.1)-(4.4), табл.9.1.

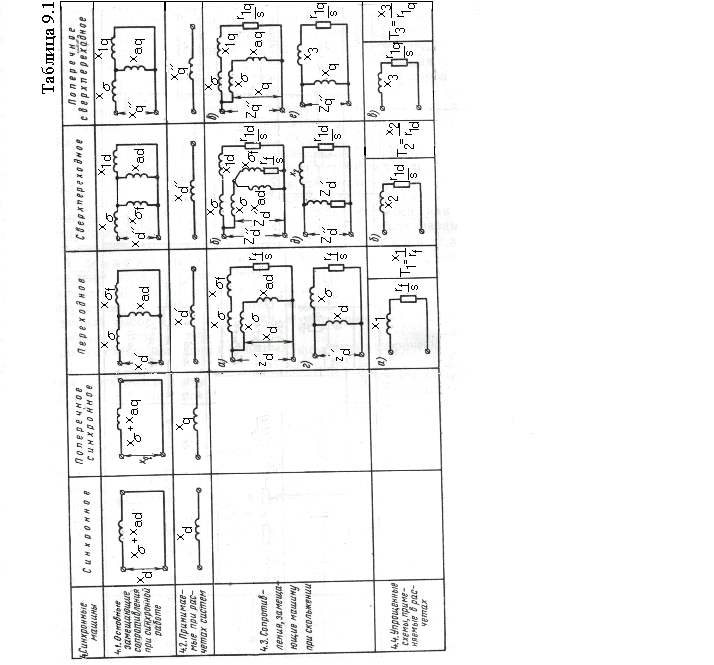Эти схемы предполагают, что синхронно работающий генератор находится или в начальной стадии переходного процесса ( ) или в установившемся режиме ( ). При асинхронном режиме (работа при скольжении ) приближенные Г-образные частные схемы для определения сопротивлений получаются на основе схем , изображенных на рис.9.12, принимая вид, показанный в графе 4.3.

Эти схемы аналогичны упрощенной Г-образной схеме замещения (рис.2.11) асинхронного двигателя.

Дальнейшее упрощение заключается в отбрасывании ветви намагничивания аналогично тому, как это было сделано ранее для асинхронного двигателя. После этого схемы приобретают вид схем, приведенных в графе 4.4 ( ). Входящие в них сопротивления можно выразить через основные параметры синхронного генератора. Так, рассматривая схему в графе 4.3 а в предположении, что , а также учитывая, и , получим , (9.9)

откуда . (9.10)

Аналогично из схемы графы 4.3 б будем иметь

. (9.11)

И точно таким же образом из схемы графы 4.3 в

. (9.12)

Заметим, что схемы замещения, приведенные в графе 4.4 а, б и в в основном отражают только качественно происходящие процессы. В самом деле, схема 4.4 а предполагает, что на роторе машины действует только одна короткозамкнутая обмотка возбуждения. Схема 4.4 б сооответствует такому же предположению относительно продольной демпферной обмотки, а схема 4.4 в –относительно поперечной.

Возвращаясь к определению момента условно выделенной машины и переходя, согласно (9.10) от параметров двигателя к параметрам, характеризующим синхронный генератор, и заменяя ; , получим . (9.8 а)

Зависимость этого момента от скольжения представлена на рис.9.11 характеристикой .

При малых скольжениях иногда пренебрегают величиной и грубо представляют (9.8 б)

Уточнение формул асинхронного момента

У синхронного генератора обмотка возбуждения расположена не равномерно по всему ротору, как это было принято при выводе (9.8 а), а только по продольной оси. Кроме этой обмотки, по этой же оси действует продольная демпферная обмотка, а по оси - поперечная демпферная обмотка. Будем, аналогично тому как это делалось при выводе формулы (9.8), определять момент, развиваемый в результате действия всех трех одноосных обмоток, как половину суммы моментов трех асинхроннывх машин, у каждой их которых имеются соответствующие распределенные обмотки (рис.9.13):