25.Порядок расчета времени отключения трехфазного короткого замыкания в начале или в конце двухцепной линии электропередачи.

26.Порядок расчета динамической устойчивости двух электростанций, работающих параллельно на общую нагрузку.

Принципиальная схема для случая параллельной работы двух электростанций показана на рис.8.8.

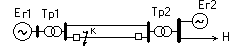
Рис.8.8. Принципиальная схема системы с двумя электростанциями

Первый вопрос, который возникает в связи с этой схемой электропередачи, это вопрос об учете характеристик нагрузки. При исследовании статической устойчивости узла нагрузки было установлено, что изменение скольжения асинхронных двигателей в зависимости от напряжения приводит к сложным, нелинейным статическим характеристикам нагрузок .

В этой связи в упрощенных расчетах неизбежным шагом является замещение нагрузки постоянным комплексным сопротивлением, что в сущности предполагает постоянство скольжения двигателей.

Значение сопротивления нагрузки может быть определено в зависимости от напряжения в точке ее включения при нормальном режиме по формуле:

Z_H , (8.24)

где - полная мощность нагрузки; - коэффициент мощности нагрузки.

При представлении нагрузки постоянным комплексным сопротивлением схема замещения в случае двух генераторов имеет вид, показанный на рис.8.8 а.

При к.з. в начале одной из цепей в точке к.з. оказывается включенным эквивалентное шунтирующее сопротивление к.з. , состоящее в общем случае из сопротивлений схем замещения обратной и нулевой последовательности (рис.8.8 б).

При отключении поврежденной линии шунтирующее сопротивление к.з. исключается из схемы вместе с сопротивлением отключаемой цепи.

Рис.8.8. Схемы замещения системы в различных режимах:

а - нормальный режим; б - при к.з.; в - при отключении к.з.

Короткое замыкание сопровождается внезапным изменением отдаваемой мощности. Роторы генераторов получают положительное или отрицательное ускорение и их роторы начинают перемещаться относительно друг друга.

Отдаваемая обоими генераторами мощность зависит от параметров системы и от угла между их роторами, но не зависит от абсолютных значений углов и каждого из генераторов в отдельности. Поэтому устойчивость системы определяется исключительно относительным углом расхождения роторов а не абсолютными значениями углов и , ориентированными относительно какой-либо оси отсчета (например, относительно вектора напряжения на шинах нагрузки).

Максимальный угол расхождения роторов в случае двух генераторов можно найти с помощью несколько видоизмененного правила площадей. Для этого следует построить графики изменения активной мощности первой и второй станций в зависимости от угла между ЭДС и ( то есть от угла ) для условий работы до к.з., при к.з. и после отключения поврежденного участка.

Для этой цели следует воспользоваться выражениями мощности через собственные и взаимные проводимости ветвей для двух источников, заменив на и изменив знак мощности у второго источника, поскольку в данном случае в конце системы расположена электростанция, для которой за положительное направление мощности должно быть принято то же направление, что и для станции, расположенной в начале системы, то есть от источника в цепь.

Таким образом можно записать,

(8.25)

где и - отдаваемые мощности первой и второй электростанциями. Собственные и взаимные проводимости ветвей должны быть вычислены для каждой из трех схем, приведенных на рис.8.8, соответствующих различным режимам работы, где генераторы должны быть представлены переходными индуктивными сопротивлениями . Электродвижущие силы за переходными сопротивлениями и сохраняют одни и те же значения во всех трех режимах и определяются по условиям нормального режима.

Н а рис.8.9 показаны характеристики мощностей и при различных режимах.

Рис.8.9. Характеристики мощности электростанций в различных режимах:

1 – нормальный режим; 2 – при к.з.; 3 – отключение к.з.

Пусть до момента к.з. угол между ЭДС обеих станций был равен и мощности электростанций соответственно и (точки и на кривых и на рис.8.9). В момент к.з. угол вследствие инерции роторов обеих станций остается неизменным и режиму отвечают характеристики 2, построенные для к.з. (точки и ).

Из рис.8.9 видно, что одна из станций (первая) при к.з. сбрасывает нагрузку, другая, наоборот, ее воспринимает. Благодаря этому роторы генераторов первой станции будут ускоряться, а второй – замедляться.

Такое распределение мощностей является типичным, но не единственно возможным. В некоторых случаях, например, при к.з. вблизи точки включения нагрузки, возможен сброс мощности обеими станциями.

Ускорения роторов машин обеих станций в относительных единицах будут равны:

где постоянные инерции выражены в радианах.

Если же ускорения выразить в градусах в секунду в квадрате, то

, (8.26)

где и выражены в секундах; ( ).

Относительное ускорение между роторами генераторов обеих станций определяется как разность их абсолютных ускорений:

(8.27)

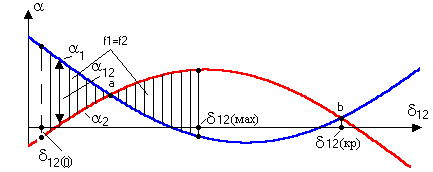С помощью рис.8.9 или, используя зависимости (8.25), можно найти изменение избытков мощности и в зависимости от угла . После этого нетрудно построить кривые зависимости изменения абсолютных ускорений и от этого угла (рис. 8.10).

Рис. 8.10. Зависимости ускорений электростанций от относительного угла

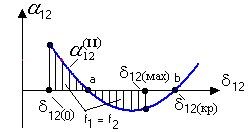Ординаты, заключенные между этими кривыми, дают относительное ускорение . Получаемая отсюда зависимость ускорения от угла приведена на рис.8.11.

Рис.8.11. Зависимость относительного ускорения от относительного угла

Относительное ускорение равно первой производной относительной угловой частоты вращения по времени:

но производная определяет собой относительную угловую частоту вращения и, следовательно, Интегрируя это выражение, получаем:

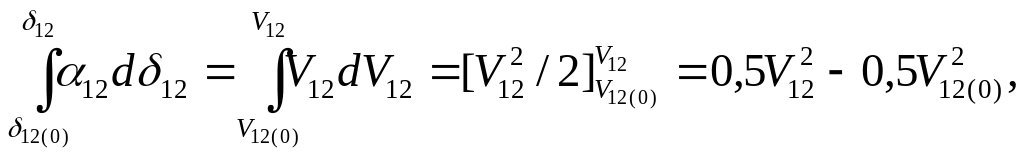
а так как начальная относительная угловая частота вращения равна нулю, то

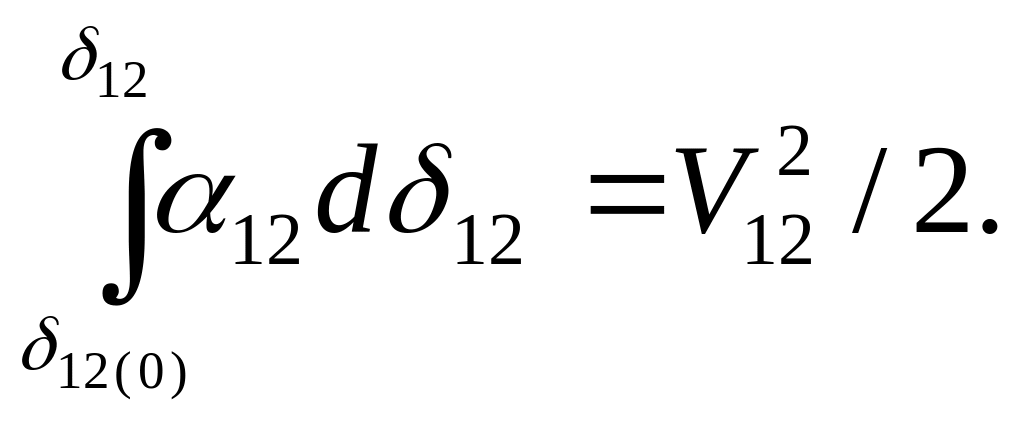(8.28)

Левая часть этого выражения определяет площадь, ограниченную кривой на рис.8.11. Как вытекает из (8.28), эта площадь пропорциональна квадрату относительной угловой частоты вращения роторов генераторов.

До точки (рис.8.11) относительное ускорение положительно, относительная угловая частота увеличивается и в точке достигает максимума. За этой точкой относительное угловое ускорение отрицательно и относительная угловая частота начинает уменьшаться. Когда площади положительного и отрицательного относительного угловых ускорений будут равны друг другу и, следовательно, интеграл 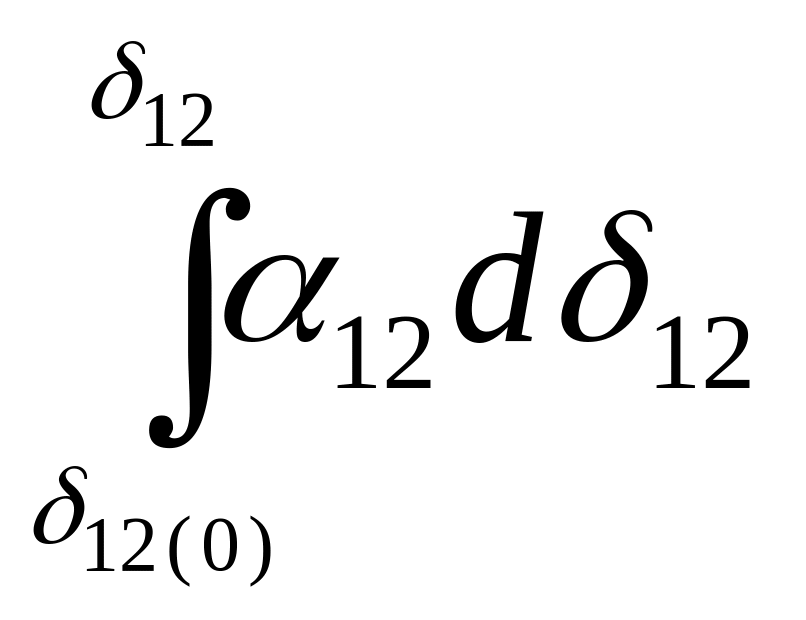сделается равным нулю, относительная угловая частота будет также равна нулю. В этот момент угол расхождения роторов генераторов достигает максимума и в дальнейшем будет уменьшаться. Таким образом, максимальное значение угла расхождения можно определить графически, исходя из равенства площадей относительного ускорения и торможения. Площадь, ограниченная участком кривой между точками и , является максимально возможной площадью относительного торможения. Отношение этой площади к площади ускорения дает коэффициент запаса динамической устойчивости системы. Если максимально возможная площадь торможения получается меньше площади ускорения, то система выпадает из синхронизма, так как за точкой относительная угловая частота снова начинает возрастать. При достаточно быстром отключении поврежденной цепи здесь опять можно достигнуть значительного увеличения устойчивости.

Для режима работы с отключенной цепью так же, как и при к.з., можно построить кривую зависимости относительного углового ускорения от угла . Эта кривая вместе с кривой, относящейся к режиму работы при к.з., дана на рис.8.12.

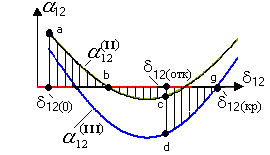
Рис.8.12.Применение правила площадей к анализу отключения к.з.

в системе, содержащей две электростанции

Сначала работа характеризуется верхней кривой. При отключении поврежденного участка в некоторой точке происходит переход рабочей точки на нижнюю кривую в точку . Благодаря этому возможная площадь относительного торможения возрастает. Предельный угол расхождения может быть определен по правилу площадей.

Для того чтобы найти предельно допустимое время отключения к.з., необходимо определить изменение угла во времени с помощью метода последовательных интервалов. Поскольку изменение избытков мощности и в зависимости от угла уже известно, это не представляет затруднений.

По (8.20) вычисляется приращение угла для обеих станций в течение первого интервала:

Затем находят значение углов и для обеих станций в конце первого интервала:

Разность этих углов дает значение угла расхождения роторов в конце первого интервала:

В зависимости от этого угла можно найти значения избытков мощности и и приращение углов во втором интервале:

Затем можно найти значение угла расхождения в конце второго интервала и т.д.

Если воспользоваться непосредственно кривой зависимости приведенной на рис.8.12, то все вычисления можно сократить примерно вдвое. Приращения углов для обеих станций в течение первого интервала будут равны:

Разность этих приращений дает относительное приращение угла :

но из (8.26) имеем:

,

и, следовательно,

(8.29)

Совершенно аналогично можно показать, что приращение угла между станциями во втором и последующих интервалах будут:

или (8.30)

Таким образом, оказывается возможным вести расчет непосредственно для угла , опустив вычисления угловых перемещений для каждой станции в отдельности.