21.Учет параметров синхронных машин в расчетах динамической устойчивости.

При решении проблемы динамической устойчивости приходиться иметь дело с переходными процессами, возникающими при аварии в электричес-

кой системе, например при к.з. В этих условиях характеристики и парамет-

ры схем замещения синхронных генераторов (и других синхронных машин) должны отражать влияние переходных электромагнитных процессов в их цепях.

Как известно, в начальный момент нарушения режима синхронная маши-

на может быть представлена переходной э.д.с. и переходной реактивностью (при отсутствии демпферных обмоток на роторе).

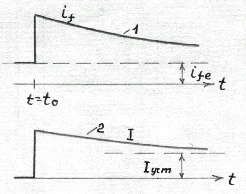Скачки токов ротора ( ) и статора ( ) в начальный момент к.з. показаны на рис.7.10.

Рис.7.10. Изменения токов при к.з.:

1) тока возбуждения; 2) огибающей тока статора

В дальнейшем свободный ток, появившийся в цепи возбуждения и не поддерживаемый напряжегнием возбудителя, начинает затухать. Вместе с ним затухает и ток статора. При этом ток возбуждения стремиться к своему первоначальному значению , пропорциональному напряжению возбудителя.

По мере затухания свободного тока в цепи возбуждения реакция якоря проявляется полностью.Таким образом, замещение генератора переходным индуктивным сопротивлением в течение всего переходного процесса, вообще говоря, было бы неправильным.

Однако, можно указать такие условия, когда с затуханием свободных токов все же можно не считаться и ограничиться представлением генератора его переходным индуктивным сопротивлением не только в первый момент к.з., но и в течение определенного промежутка времени –практически в течение первого полуцикла качаний генератора.

Такие условия возникают прежде всего при быстром отключении к.з.

При длительности к.з. около нескольких десятых долей секунды, легко реализуемой современной релейной защитой и выключателями, и с учетом того, что постоянная времени, характеризующая затухание свободного т ока ротора, у крупных машин достигает нескольких секунд, свободные токи не успевают затухать сколько-нибудь значительно и реакция якоря не проявляется в большей мере, чем это отражается переходным индуктивным сопротивлением машины .

Те же выводы могут быть сделаны и при длительном к.з., если генератор снабжен регулятором, осуществляющем форсировку возбуждения.

Правда, свободный ток в обмотке возбуждения при длительном к.з. затухает весьма значительно, но это затухание компенсируется изменением вынужденного т ока возбуждения , пропорционального напряжению возбудителя и возрастающего вместе с ним под влияинием регулятора возбуждения (рис.7.11).

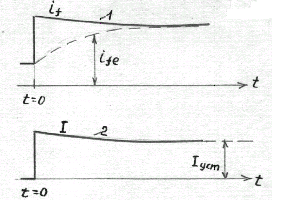Рис.7.11. Изменения токов при к.з. и наличии автоматического регулятора напряжения:

1) тока возбуждения; 2) огибающей тока статора

При достаточной скорости подъема напряжения возбудителя затухание результирующих токов ротора ( ) и статора ( ) может быть полностью устранено и значение тока статора в любой момент момент времени будет определяться переходным индуктивным сопротивлением с тем же правом, что и для первого момента к.з.

С помощью переходного индуктивного сопротивления генератора можно определять не только токи к.з., но и токи нормального режима, предшествовавшего к.з., если в качестве э.д.с. генератора ввести э.д.с. , равную , то есть прибавляя к вектору поперечной составляющей напряжения на шинах генератора в нормальном режиме вектор падения напряжения в переходном индуктивном сопротивлении от продольной состав-

ляющей тока статора нормального режима .

Если пренебречь влиянием активных сопротивлений, то при к.з. на шинах генератора, работавшего до того в режиме холостого хода, ток к.з. отстает на от вектора э.д.с. и вектор тока совпадает с продольной осью машины , то есть (рис.7.12). Поперечная составляющая тока к.з. при этом отсутствует.

Рис.7.12. Векторная диаграмма при к.з.

Именно эти условия, когда переходный процесс протекает в продольной оси, и рассматривались выше.

Известно, что в переходном процессе претерпевают изменения как продольная, так и поперечная составляющие тока статора.

В связи с отсутствием замкнутых обмоток в поперечной оси машины (если не считаться с наличием демпферной обмотки) магнитный поток реакции якоря в ее поперечной оси изменяется, свободно следуя за изменением поперечной составляющей тока статора, и, следовательно, поперечное индуктивное сопртивление генератора в переходном процессе должно полностью содержать составляющую поперечной реакции якоря.

Иными словами, поперечное индуктивное сопротивление генератора в переходном процессе должно быть равно синхронному поперечному индуктивному сопротивлению .

Таким образом, с некоторыми оговорками генератор в переходном процессе может быть замещен в продольной оси переходным индуктивным сопротивлением и э.д.с. и в поперечной оси синхронным индуктивным сопротивлением .

Это относится к любому внезапному нарушению режима работы синхронной машины, связанному не только с коммутационными явлениями в цепи генератора, но и с изменениями частоты вращения и углового сдвига ротора .

Так, например, если допустить весьма быстрое изменение угла , характеризующего относительное положение ротора генератора, работающего на шины бесконечной мощности, то при пересечении магнитного потока реакции якоря в обмотке возбуждения возникают свободные токи, компенсиру-

ющие изменение продольной составляющей потока реакции так же, как и при к.з.

Принцип постоянства потокосцепления обмотки возбуждения позволяет и в этих условиях характеризовать генератор индуктивными сопротивлениями и и э.д.с. .

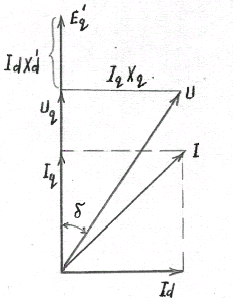Векторная диаграмма генератора при этом имеет вид, изображенный на рис.7.13.

Рис.7.13. Векторная диаграмма синхронной машины,

представленной сопротивлениями и

Она аналогична векторной диаграмме явнополюсной машины с индуктивным сопротивлением в продольной оси и э.д.с. .

Согласно выражения (5.4) зависимость активной мощности машины с такими параметрами от угла имеет вид:

(7.1)

Таким образом, характеристика мощности помимо основной гармоники

имеет и вторую гармонику .

Коэффициент - отрицателен, поскольку , что обусловливает смещение максимума характеристики активной мощности в область углов, больших .

В практических расчетах зачастую опускают вторую гармонику, предполагая, что индуктивные сопротивления в продольной и поперечной осях одинаковы и равны . При этом вместо э.д.с. и угла в расчет вводятся некоторые фиктивные величины э.д.с. и угла (рис.7.14) и тогда характеристика мощности может быть рассчитана по выражению:

. (7.2)

В дальнейшем, там, где это не вызовет недоразумений, используя выражение (7.2), мы не будем писать индекс “ ' “ у э.д.с. и угла, но следует помнить, что речь идет о фиктивных значениях этих величин.

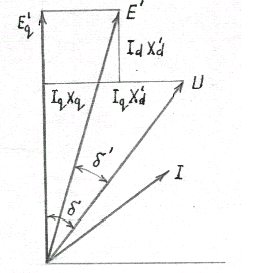Рис.7.14. Определение фиктивных э.д.с. и угла на векторной диаграмме