20.Схемы замещения при коротких замыканиях в расчетах динамической устойчивости.

Если отвлечься от вопроса о параметрах генераторов при различных условиях их работы, то схема замещения системы передачи при трехфазном металлическом к.з. (рис.7.7, в) отличается от схемы замещения нормального режима (рис.7.7, б) лишь тем, что точка к.з. (в однолинейной схеме замещения) непосредственно замыкается на обратный (нулевой) провод.

Рис.7.7. Принципиальная схема (а) и схемы замещения электропередачи

при нормальном режиме (б) и при трехфазном к.з. (в)

Напряжение в точке к.з. при этом падает до нуля и передача мощности приемной системе через нее оказывается невозможной.

Если трехфазное к.з. произошло в начале или конце двухцепной ЛЭП, то генератор сбрасывает активную мощность почти до нуля, покрывая только потери мощности в активных сопротивлениях электропередачи.При этом избыток мощности, развиваемый турбиной, а, следовательно, и избыточный момент на валу агрегата турбина-генератор получаются значительными, чем и объясняется большая вероятность нарушения устойчивости при трехфазном к.з.Мощность турбины остается при этом неизменной и равной , так как ее регулятор реагирует только на изменение частоты вращения агрегата: турбина-генератор, которая в момент отключения цепи сохраняет свое прежнее значение .

При несимметричных к.з. дело обстоит несколько иначе.Прежде всего установим некоторые принципиальгные положения, которыми следуется руководствоваться при исследовании динамической устойчивости при несимметричных к.з.

Нужно помнить, что качания роторов генераторов обусловлены только изменениями их активной мощности и поэтому при несимметричных к.з. нас будут интересовать те стороны вопроса, которые непосредственно вли- яют на значения активных мощностей и моментов на валах машин.

Современная практика при исследовании несимметричных режимов неизменно обращается к методу симметричных составляющих, который позволяет наметить наиболее простые пути решения задачи и в данном случае.

Разлагая токи и напряжения при несимметричном к.з. на составляющие прямой, обратной и нулевой последовательностей, можно сразу констатировать, что при к.з. в сети высшего напряжения токи нулевой последовательности в цепи генератора вообще не циркулируют, поскольку при обычном соединении обмоток повысительных трансформаторов по схеме треугольник-звезда с заземленной нейтралью токи нулевой последовательности замыкаются на землю через заземленную нейтраль трансформатора.

Иначе обстоит дело с токами обратной последовательности, которые трансформируются вне зависимости от схемы соединения обмоток трансформаторов (так же как и токи прямой последовательности) и протекают, следовательно, в обмотке генератора при несимметричном к.з. в любой точке сети.

Токи обратной последовательности создают в воздушном зазоре машины магнитный поток реакции якоря, вращающийся в направлении, обратном направлению вращения ротора, и имеющий, следовательно, двойную частоту вращения относительно ротора.

Возникающий при этом вращающий момент обратной последовательностит изменяется периодически с двойной частотой. В связи с тем, что механическая инерция вращающихся частей агрегата:турбина-генератор велика, то они не успевают следовать за периодическими колебаниями момента столь высокой частоты (100 Гц).

Среднее же значение момента обратной последовательности близко к нулю.

Кроме того, на основной синхронный магнитный поток в воздушном зазоре, а следовательно, и на основную гармонику э.д.с. прямой последовательности токи обратной последовательности почти не оказывают влияния.

Таким образом, при несимметричных к.з. оказывается возможным не считаться с возникновением моментов генератора, связанных с токами обратной и нулевой последовательности, и ограничиться рассмотрением токов и напряжений только прямой последжовательности.

Полученный вывод очень важен, так как позволяет значительно упростить анализ динамической устойчивости при несимметричных к.з. При этом оказывается возможным перейти к рассмотрению от несимметричного режима работы системы к симметричному согласно правилу эквивалентности прямой последовательности.

Полученные результаты не следует понимать таким образом, что параметры схем замещения обратной и нулевой последовательностей вообще не влияют на устойчивость электрических систем при несимметричных к.з.

Как известно, схемы замещения прямой , обратной и нулевой последовательностей связаны между собой, образуя комплексные схемы замещения для соответствующих несимметричных к.з.

Таким образом, токи и напряжения в комплексной схеме замещения зависят от сопротивлений и конфигурации схем не только прямой, но также обратной и нулевой последовательностей.

На рис.7.8 приведен пример построения комплексной схемы замещения при однофазном к.з. в простой схеме электропередачи, в которой схемы замещения прямой, обратной и нулевой последовательностей, ориентированные относительно точки к.з., соединены последовательно.

Рис.7.8. Пример построения комплесной схемы замещения

при однофазном к.з. в простой электропередаче:

а) принципиальная схема электропередачи;

б) коплексная схема замещения;

в) преобразованная комплексная схема замещения

Так как значения токов, протекающих в отдельных элементах схем обратной и нулевой последовательностей для нашей задачи несущественны, то схемы замещения обратной и нулевой последовательностей можно преобразовать к виду результирующих сопротивлений и , как это показано на рис.7.8, в.

Полученная схема замещения при однофазном к.з. отличается от схемы замещения нормального режима работы системы лишь тем, что в точке к.з. оказывается включенным шунтирующее сопротивление, равное сумме и .

Таким образом, если рассматривать только составляющие прямой последовательности, то однофазное к.з. сводится к включению в точке к.з. трехфазного симметрично шунтирующего сопротивления , составленного из последовательно соединенных сопротивлений и .

Используя комплексные схемы замещения, можно установить, что это положение справедливо и для других видов несимметричного к.з. с той только

разницей, что шунтирующее сопротивление при двухфазном к.з. (без замыкания на землю) равно результирующему сопротивлению схемы замещения обратной последовательности, а при двухфазном замыкании на землю – результирующим сопротивлениям схем замещения обратной и нулевой последовательностей, сложенным параллельно.

Очевидно, для симметричного трехфазного к.з. шунтирующее сопротивление равно нулю.

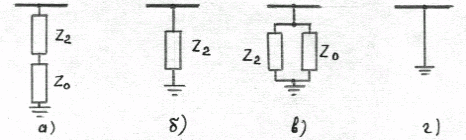Оценивая различные виды к.з. с точки зрения сохранения динамической устойчивости системы (рис.7.9), можно видеть, что наиболее тяжелым из них является трехфазное к.з., так как в этом случае сопротивление эквивалентного шунтирующего сопротивления, а следовательно, и напряжение в точке к.з. равны нулю.

Рис.7.9. Схема шунтирующего сопротивления в месте к.з.:

а) при однофазном к.з.; б) при двухфазном к.з.;

в) при двухфазном к.з. на землю; г) при трехфазном к.з.

Двухфазное к.з. на землю является более благоприятным в указанном смысле. Далее идет двухфазное к.з. без замыкания на землю и , наконец, однофазное к.з. В последнем случае шунтирующее сопротивление получается наибольшим.