17. Устойчивость синхронного двигателя при изменении уровня и частоты питающего напряжения.

На основе выражений для момента и мощности синхронной машины, приведенных выше (см.(2.9) и (2.10)), можно получить статические и разного рода динамические характеристики.

При изменении напряжения, подведенного к синхронному двигателю (СД), его активная мощность и вращающий момент изменяются прямо пропорционально величине напряжения, если не учитывать потери в статоре:

и .

Изменение частоты подведенного напряжения изменяет вращающий момент:

, (6.8)

где - характеризует систему возбуждения СД; - определено при ; .

У явнополюсных СД имеется еще момент явнополюсности, который пропорционален квадрату напряжения и обратно пропорционален частоте:

.

Величина момента СД, если не учитывать насыщение, пропорциональна току ротора. СД обычно работает при угле и поэтому обладает значительной перегрузочной способностью ; у некоторых специальных СД .

Реактивная мощность СД, определенная упрощенно (без учета потерь в статоре) .

При - СД выдает реактивную мощность в сеть; при

-СД потребляет реактивную мощность из сети.

Статические характеристики СД имеют вид, показанный на рис.6.26, где представлены зависимости активной и реактивной мощностей от режима системы.

Рис.6.26. Статические характеристики синхронного двигателя при изменении

напряжения на выводах статора,имеющего независимое возбуждение:

1,2,3) реактивная мощность, выдаваемая двигателем при постоянном

нагрузочном моменте на валу ;4) зависимость максимального

момента от напряжения U

18.Вторичные признаки устойчивости комплексной нагрузки.

Формальным признаком устойчивости АД при постоянстве тормозного момента является положительный знак прозводной вращающего момента по скольжению . Однако вычисление этой прооизводной возможно лишь при условии представления множества двигателей нагрузки одним эквивалентным двигателем.

Определение параметров эквивалентного двигателя представляет собой сложную задачу, что заставляет искать другие решения, позволяющие подойти к оценке устойчивости группы асинхронных двигателей в электрических системах, не выделяя их отдельно в составе комплексной нагрузки, а используя, например, уже известные нам статические характеристики комплексной нагрузки.

Статические характеристики комплексной нагрузки дают зависисимости активной и реактивной мощностей потребителей, входящих в состав нагрузки, включая также и асинхронные двигатели, от напряжения в точках включения нагрузки.

Использование этих характеристик не исключает возможность рассмотрения скольжения двигателей, характер изменения которого и позволяет судить об устойчивости двигателей.

Следует иметь в виду, что при построении статических характеристик нагрузки каждому значению напряжения на выводах эквивалентного двигателя всегда соответствует свое значение скольжения (рис.6.6) и, следовательно, зависимости отражают изменение скольжения асинхронных двигателей.

В числе вторичных признаков устойчивости комплексной нагрузки, использующих характеристики нагрузки можно указать на знак производных и некоторые другие, изменяющие знак вместе с производной .

Производная определяется по касательной к характеристике , которая легко может быть построена при любом характере связи между генератором и нагрузкой.

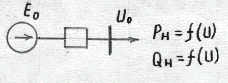Пусть в исходном режиме в схеме замещения на рис.6.27 э.д.с. генератора равна и напряжение на нагрузке .

Рис.6.27. Система с нагрузкой, заданной статическими характеристиками

Задаваясь новым значения напряжения на нагрузке -меньшим, чем в нормальном режиме, по статическим характеристикам нагрузки можно определить соответствующие значения активной и реактивной мощностей нагрузки и, произведя расчет режима схемы, найти новое значение э.д.с. генератора , соответствующее пониженному значению напряжения .

Выполнив расчеты для различных значений , можно построить кривую зависимости , которая имеет вид (рис.6.28).

При э.д.с генератора возможны два режима работы на характеристике - в точке а и в точке в. В первом из них производная положительна, а во втором – отрицательна.

Каждой точке характеристики соответствует свое скольжение

двигателей нагрузки, возрастающее с уменьшением напряжения .

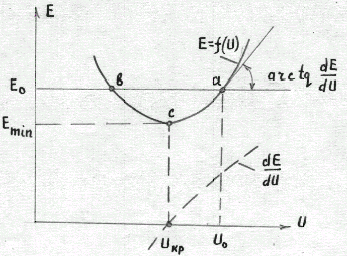
Рис.6.28. Зависимость э.д.с. генератора от напряжения на шинах нагрузки

Е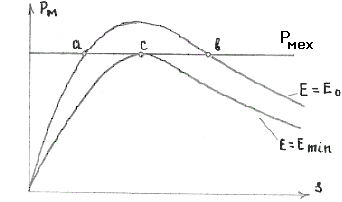 сли обратиться к зависимости момента или мощности эквивалентного двигателя нагрузки от скольжения (рис.6.29), то точки а и в возможных режимов на характеристике определятся на графике зависимости при ее пересечении с горизонтальной характеристикой тормозной мощности .

Рис.6.29. Характеристики активной мощности

эквивалентного асинхронного двигателя

при различных значениях э.д.с. генератора

При этом становится очевидным, что точка а (в которой производная ) определяет устойчивый режим работы эквивалентного двигателя, а точка в (где ) – неустойчивый.

При уменьшении э.д.с. генератора характеристика мощности эквивалентного двигателя понижается, и при минимальном возможном значении э.д.с. (точка с на характеристике на рис.6.28) график мощности касается горизонтальной характеристики тормозной мощности в точке с (рис.6.29). При этом, очевидно, достигается предельный режим с точки зрения устойчивости эквивалентного двигателя.

Таким образом, оказывается возможным по знаку производной судить об устойчивости группы асинхронных двигателей, входящих в состав комплексной нагрузки. Для этого достаточно построить график по методике, изложенной выше, используя статические характеристики комплексной нагрузки.

Запас устойчивости группы двигателей в исходном режиме (точка на рис. 6.28) можно оценить по отношению , где - напряжение на шинах нагрузки при ; - критическое напряжение, достигаемое в точке минимума графика .

Построение характеристик, связывающих изменение напряжения с э.д.с., достаточно просто решает задачу и при большем числе нагрузок в системе.

Одни и те же расчеты позволяют установить значения напряжений на всех нагрузках при различных величинах э.д.с. генератора.

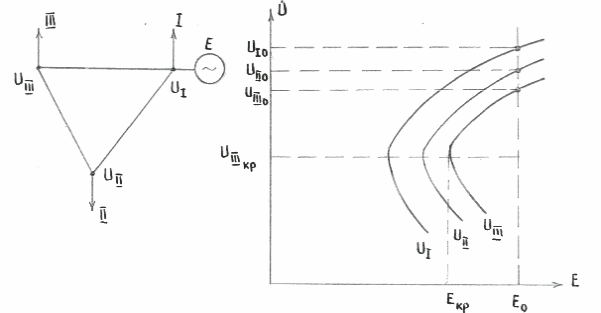Построив графики зависимостей этих напряжений от э.д.с. генератора (рис.6.30), можно установить момент неустойчивости той нагрузки, для которой критическое значение э.д.с. получается наибольшим. Расчеты удобно вести, задаваясь значением напряжения на наиболее удаленной из нагрузок.

Рис.6.30. Зависимости напряжений на нагрузках от э.д.с. генератора

Можно строго доказать, что перемена знака производной , устанавливающая момент неустойчивости группы асинхронных двигателей, влечет за собой изменение знака не только производной , но также производной .

В отношении производной мы ограничимся здесь изложением некоторых общих соображений, позволяющих судить о возможности использования знака этой производной для оценки устойчивой работы группы асинхронных двигателей.

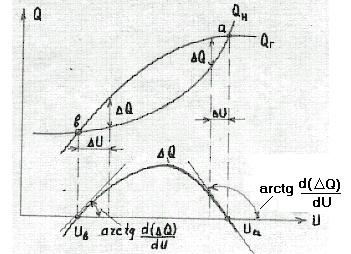На рис.6.31 показаны зависимости реактивной мощности генератора и нагрузки от величины напряжения на нагрузке.

Рис.6.31.Характеристики реактивной мощности генератора и нагрузки

при определении небаланса

Характеристика реактивной мощности нагрузки представляет собой обычную статическую характеристику . Характеристика реактивной мощности генератора может быть вычислена при неизменной э.д.с. генератора в зависимости от напряжения при условии, что активная мощность генератора изменяется в соответствии с активной мощностью нагрузки ( ), причем последняя следует за напряжением согласно статической характеристике .

Примечание:

Расчет характеристики может быть выполнен с помощью уравнений (2.9)- (2.10). При этом из второго уравнения (2.9) при принятом значении и отвечающей ему величине мощности , найденной по статической характеристике, определяется угол . После этого по второму

уравнению (2.10) вычисляется реактивная мощность . Эта мощность поступает со стороны генератора к нагрузке, поэтому на рис.6.31 и 6.32 она отмечена как . Однако следует подчеркнуть, что это не мощность самого генератора и поэтому она не может быть рассчитана по первому уравнению (2.10).

Построенные графики на рис.6.31 имеют две точки пересечения, характеризующие возможные режимы работы при данной э.д.с генератора (точка и на рис. 6.31). В этих точках балансируются как активные, так и реактивные мощности генератора и нагрузки.Эти точки совпадают , очевидно, с одноименными точками и на характеристике активной мощности (момента) двигателя (рис.6.29), в которых балансируются вращающий и тормозной моменты двигателя при э.д.с. генератора .

Следовательно, точка (пересечения характеристик реактивной мощности генератора на рис. 6.31) определяет устойчивый режим работы эквивлентного двигателя, а точка - неустойчивый.

Характер изменения реактивной мощности генератора и нагрузки с напряжением неодинаков для точек и (рис.6.31).

Если исходный режим работы устойчив и определяется точкой то при подключении к нагрузке некоторой небольшой индуктивной проводимости (рис.6.32), потребляющей реактивную мощность и нарушаю- щей, следовательно, в точке баланс реактивной мощности генератора и нагрузки, напряжение уменьшается на .

Рис.6.32. Нарушение баланса реактивной мощности

при подключении реактивной проводимости

Это вытекает рассмотрения рис.6.31, где положительному значению в точке соответстввует отрицательное приращение . Нетрудно видеть, что для точки производная отрицательна.

Если же исходный режим существовал в точке и был неустойчив, то здесь, как следует из графика рис.6.31, производная положи- тельна.

Таким образом в качестве вторичного признака устойчивости группы двигателей может быть использовано также и условие .