Основы молекулярной физикии и термодинамики.

1.Статистический и термодинамический методы исследования макроскопических систем.Состояние систем.Процессы.

Молекулярная физика и термодинамика — разделы физики, в которых изучаются макроскопические процессыв телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (молекулярно-кинетический) и термодинамический.Первый лежит в основе молекулярной физики, второй — термодинамики. Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощьюстатистического метода.Этот метод основан на том, что свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энергии и т.д.). Например, температура тела определяется скоростью беспорядочного движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул. Термодинамика имеет дело с термодинамической системой— совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой). Основа термодинамического метода — определение состояния термодинамической системы. Состояние системы задаетсятермодинамическими параметрами (параметрами состояния) — совокупностью физических величин, характеризующих свойства термодинамической системы. Обычно в качестве параметров состояния выбираюттемпературу, давление и удельный объем. Параметры состояния системы могут изменяться. Любое изменение в термодинамической системе, связанное с изменением хотя бы одного из ее термодинамических параметров, называется термодинамическим процессом.Макроскопическая система находится в термодинамическом равновесии, если ее состояние с течением времени не меняется (предполагается, что внешние условия рассматриваемой системы при этом не изменяются).

2. Идеальный газ-простейшая статистическая система.Основное уравнение молекулярной-кинетической теориигазов для давления.

ИДŘАЛЬНЫЙ ГАЗ, теоретическая модель газа; в которой пренебрегают размерами частиц газа, не учитывают силы взаимодействия между частицами газа, предполагая, что средняя кинетическая энергия частиц много больше энергии их взаимодействия, и считают, что столкновения частиц газа между собой и со стенками сосуда абсолютно упругие.  Вывод основного уравнения. Вычислим давление газа на стенкуCD сосуда ABCD площадью S, перпендикулярную координатной оси OX(рис.8.13).

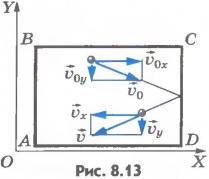
   При ударе молекулы о стенку ее импульс изменяется:  . Так как модуль скорости молекул при ударе не меняется, то  . Согласно второму закону Ньютона изменение импульса молекулы равно импульсу подействовавшей на нее силы со стороны стенки сосуда, а согласно третьему закону Ньютона таков же по модулю импульс силы, с которой молекула подействовала на стенку. Следовательно, в результате удара молекулы на стенку подействовала сила, импульс которой равен  .    Молекул много, и каждая из них передает стенке при столкновении такой же импульс. За секунду они передадут стенке импульс  ,  где Z - число столкновений всех молекул со стенкой за это время. Число очевидно, прямо пропорционально концентрации молекул, т. е. числу молекул в единице объема. Кроме того, число Z пропорционально скорости молекул  . Чем больше эта скорость, тем больше молекул за секунду успеет столкнуться со стенкой. Если бы молекулы «стояли на месте», то столкновений их со стенкой не было бы совсем. Кроме того, число столкновений молекул со стенкой пропорционально площади поверхности стенки S:  . Надо еще учесть, что в среднем только половина всех молекул движется к стенке. Другая половина движется в обратную сторону. Значит, число ударов молекул о стенку за время 1 с   и полный импульс, переданный стенке за 1 с, равен:

   Согласно второму закону Ньютона изменение импульса любого тела за единицу времени равно действующей на него силе:  .    Учтем, что не все молекулы имеют одно и то же значение квадрата скорости  . В действительности средняя за секунду сила, действующая на стенку, пропорциональна не  , а среднему квадрату скорости  :  . Так как согласно формуле (8.13)  , то  . Таким образом, давление газа на стенку сосуда равно:

   Это и есть основное уравнение молекулярно-кинетической теории газов.    Формула (8.14) связывает макроскопическую величину - давление, которое может быть измерено манометром, - с микроскопическими величинами, характеризующими молекулы: их массой, скоростью хаотичного движения.    Связь давления со средней кинетической энергией молекул. Если через   обозначить среднюю кинетическую энергию поступательного движения молекулы  то уравнение (8.14) можно записать в виде

Клапейрона - Клаузиуса уравнение

        термодинамическое уравнение, относящееся к процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно К. — К. у., Теплота фазового перехода (например, теплота испарения, теплота плавления) при равновесно протекающем процессе определяется выражением

          , (1)

         где Т — температура перехода (процесс изотермический), dp/dT — значение производной от давления по температуре при данной температуре перехода, (V₂—V₁) — изменение объёма вещества при переходе его из первой фазы во вторую.