30.Частные производные высших порядков. Теорема о равенстве смешанных производных.

 Функцию многих аргументов U=F(X1, …, хN) можно дифференцировать по каждому аргументу. Полученные частные производные  (первого порядка) обычно зависят от тех же аргументов и каждую из них также можно дифференцировать по каждому аргументу.

Частные производные от частных производных первого порядка называются Частными производными второго порядка.

Обозначение.

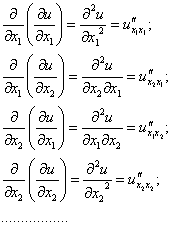Частные производные от частных производных второго порядка называются Частными производными третьего порядка.

Аналогично определяются и обозначаются частные производные четвертого, пятого и других высших порядков.

Замечание. Частные производные высших порядков, отличающиеся только последовательностью дифференцирования, равны, если они непрерывны.

Частные производные высших порядков находятся путем последовательного нахождения одной производной вслед за другой по правилам дифференцирования функции одной переменной.

Определение смешанной производной

Пусть дана достаточно гладкая (скалярная) функция   многих переменных:

Мы можем взять частную производную этой функции по одному из аргументов  , считая остальные аргументы постоянными параметрами. В результате мы получим новую функцию:

Эта новая функция тоже зависит от остальных аргументов как от параметров. То есть численное значение   в общем случае зависит от тех же переменных  , что и оригинальная функция  :

Если функция   окажется достаточно гладкой, то мы можем и её продифференцировать, взяв частную производную по тому же самому или по другому аргументу  :

Если  , то выражение в правой части равенства (4) называется смешанной производной.

Основа теоремы

Для достаточно гладкой функции многих переменных значение смешанной производной не зависит от порядка дифференцирования:

Теорема является базовой в теории функций многих переменных и широко применяется в математической физике, теории дифференциальных уравнений в частных производных, дифференциальной геометрии.

31.Экстремумы функций двух переменных.

Функция z = f(x,y) имеет максимум в точке M₀(x₀;y₀), если f(x₀;y₀) > f(x;y) для всех точек (x;y), достаточно близких к точке (x₀;y₀) и отличных от неё. Функция z = f(x,y) имеет минимум в точке M₀(x₀;y₀), если f(x₀;y₀) < f(x;y) для всех точек (x;y), достаточно близких к точке (x₀;y₀) и отличных от неё. Максимум и минимум функции называются экстремумами функции.  Исследование функции двух переменных на экстремум проводят по следующей схеме.  1. Находят частные производные dz/dx и dz/dy.  2. Решают систему уравнений:

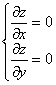
и таким образом находят критические точки функции.  3. Находят частные производные второго порядка:

4. Вычисляют значения этих частных производных второго порядка в каждой из найденных в п.2 критических точках M(x₀;y₀).

5. Делаю вывод о наличии экстремумов:  а) если AC – B² > 0 и A < 0 , то в точке M имеется максимум;  б) если AC – B² > 0 и A > 0 , то в точке M имеется минимум;  в) если AC – B² < 0, то экстремума нет;  г) если AC – B² = 0, то вопрос о наличии экстремума остается открытым;