24.Эллипс; каноническое уравнение, исследование кривой.

Эллипс – геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек F₁,F₂(фокусы) есть величина постоянная, равная 2a.

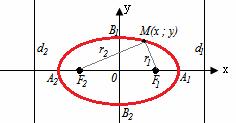
Элементы эллипса:  A₁A₂=2a - большая ось  B₁B₂=2b - большая ось  A₁ ,A₂ , B_{1 ,}B_{2 ,} - вершины  F₁(c ; 0), F₂(-c ; 0) - фокусы  F₁F₂=2c - фокальное расстояние

c²=a²-b²

 - эксцентриситет. Эксцентриситет эллипса можно рассматривать, как меру его «вытянутости»: чем больше эксцентриситет, тем меньше отношение    r₁=a-εx, r₂= a+εx - фокальные радиусы   - директрисы

Каноническое уравнение эллипса (координатные оси совпадают с осями эллипса):

Параметрические уравнения:

25.Гипербола.

Гипербола - геометрическое место точек, для каждой из которых модуль разности расстояний от нее до двух данных точек F₁,F₂ (фокусы) есть величина постоянная, равная 2a.

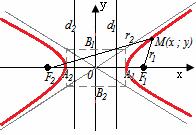
Элементы гиперболы:  A₁A₂=2a - действительная ось  B₁B₂=2b - мнимая ось  A₁ ,A₂ - вершины  F₁(c ; 0), F₂(-c ; 0) - фокусы  F₁F₂=2c - фокальное расстояние

c²=a²-b²

 - асимптоты   - эксцентриситет. Его можно рассматривать, как числовую характеристику величины раствора угла между асимптотами.  r₁=±(εx-a), r₁=±(εx+a), - фокальные радиусы (верхний знак соответствует правой, нижний – левой ветви)   - директрисы  Каноническое уравнение гиперболы (координатные оси совпадают с осями гиперболы):

Параметрические уравнения:

Уравнение гиперболы, сопряженной данной:

Действительная ось этой гиперболы равна мнимой оси другой.

26.Параболла.

Парабола – геометрическое место точек, каждая из которых равноудалена от данной точки (фокус) и от данной прямой (директриса)

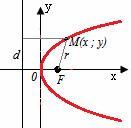
Элементы параболы:  0F - фокальная ось  0 - вершина   - фокус  ε=1 - эксцентриситет   - фокальный радиус   - директриса   - фокальный параметр

Каноническое уравнение параболы (ось Ox совпадает с фокальной осью, начало координат – с вершиной параболы):

y²=2px . При p<0 ветви параболы направлены влево.  Если фокальная ось совпадает с осью Oy, то уравнение параболы имеет вид:

x²=2py При p>0 ветви параболы направлены вверх, при p<0 -вниз.

27.Функции двух переменных, область определения.

Если каждой паре ( x;y) значений двух независимых друг от друга переменных величин х и у из некоторого множества D соответствует единственное значение величины, то говорят, что z есть функция двух независимых переменных x и y, определенная на множестве D.

Обозначается: z=f(x;y) или z=z(x;y).

Например,   S=ab, S=S(a;b)- функции двух переменных; V=abc, V=V(a,b.c) – функция трех переменных;

A=   – функция трех переменных.

Способы задания функций нескольких переменных

Чтобы задать функцию двух (трех) переменных, нужно указать способ, с помощью которого для каждой пары (тройки) значений аргументов можно найти соответствующее значение функции. Наиболее часто функция задается аналитически  - это явное задание функции или неявное задание 

Например,  - это явно заданная функция двух переменных; уравнение   задает неявно две функции двух переменных .

Область определения функции

Непрерывное множество пар   значений независимых переменных  , при которых функция определена, называется областью определения функции.

Область определения называется замкнутой областью, если она включает в себя свою границу; открытой областью, если она не включает в себя свою границу; ограниченной областью, если может быть помещена в круг конечного радиуса.

А)Пример замкнутой ограниченной области Б)Пример замкнутой неограниченной области

В)Пример незамкнутой ограниченной области