20.Прямая в пространстве, различные виды уравнений.

Вообще, прямая линия целиком принадлежит некоторой плоскости в пространстве. Это утверждение вытекает из аксиом:

через две точки проходит единственная прямая;

если две точки прямой лежат в некоторой плоскости, то все точки прямой лежат в этой плоскости.

Существует еще одна аксиома, которая позволяет рассматривать прямую в пространстве как пересечение двух плоскостей: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

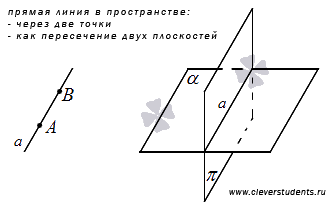
Канонические уравнения

Если известна некоторая точка пространства  , принадлежащая прямой, и направляющий вектор   данной прямой, то  канонические уравнения этой прямой выражаются формулами:

Приведённая запись предполагает, что координаты направляющего вектора   не равны нулю.

Параметрические уравнения

Если известна точка  , принадлежащая прямой, и направляющий вектор   данной прямой, то параметрические уравнения этой прямой задаются системой:

.

Нормальные уравнения.

    ,

 где    – расстояние от прямой до начала координат; a – угол между нормалью к прямой и осью 

21.Углы между плоскостями, прямыми, прямой и плоскостью.

Угол между двумя пересекающимися по прямой c плоскостями   и   – это угол между двумя пересекающимися прямыми a и b, по которым плоскости   и  пересекаются с плоскостью  , перпендикулярной к прямой c.

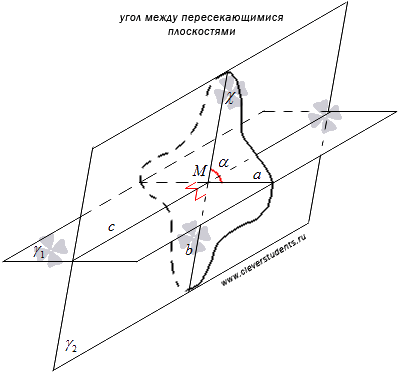
Чтобы определить угол между двумя пересекающимися прямыми нам потребуются определения, данные в статье геометрическая фигура угол и некоторые вспомогательные определения.

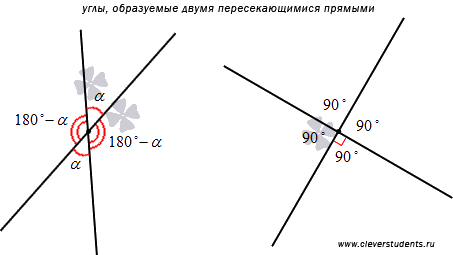
Две прямые называются пересекающимися, если они имеют одну единственную общую точку. Эта общая точка двух прямых называется точкой пересечения прямых. Точка пересечения разбивает каждую из пересекающихся прямых на два луча. Очевидно, эти лучи образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Таким образом, если нам известна мера одного из углов, образованных двумя пересекающимися прямыми, то мы можем определить меры трех остальных углов. Действительно, пусть один из углов равен углу  . Тогда вертикальный с ним угол также равен  , а смежные с ним углы равны  . Если  , то все четыре угла являются прямыми. В этом случае пересекающиеся прямые называются перпендикулярными (им посвящена статья перпендикулярные прямые).

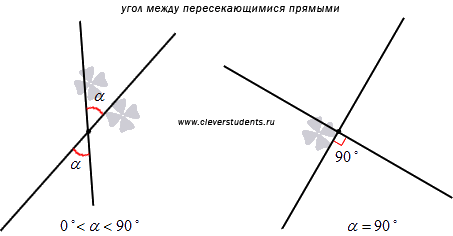
Угол между двумя пересекающимися прямыми – это мера меньшего из четырех углов, образованных этими прямыми.

Из приведенного определения следует, что градусная мера угла между двумя пересекающимися прямыми выражается действительным числом из интервала  . Угол между перпендикулярными прямыми по определению равен девяноста градусам.

К началу страницы

Угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, - это угол между прямой и ее проекцией на эту плоскость.

Определение угла между прямой и плоскостью позволяет заключить, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми: самой прямой и ее проекцией на плоскость. Следовательно, угол между прямой и плоскостью есть острый угол.

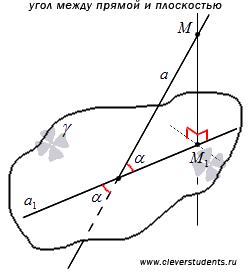
Угол между перпендикулярными прямой и плоскостью считают равным 90, а угол между параллельными прямой и плоскостью либо не определяют вовсе, либо считают равным 0.