
- •1.Задача о вычислении площади криволинейной трапеции. Определённый интеграл.
- •6.Приложения определённого интеграла (площадь фигуры, объём тела вращения).
- •7.Определители второго и третьего порядка, способы их вычисления.
- •8.Свойства определителей.
- •9.Решение слау методом Крамера.
- •10.Решение слау методом Гаусса.
- •11.Решение слау методом обратной матрицы.
- •12.Матрицы и действия с ними.
- •13.Ранг матрицы и способ его вычисления.
- •14.Обратная матрица.
- •15.Векторы на плоскости и в пространстве. Операции над векторами. Модуль вектора.
- •16.Скалярное произведение и его свойства.
- •17.Векторное произведение и его свойства.
- •18.Смешанное произведение векторов.
- •19.Плоскость в пространстве, различные виды уравнений.
- •20.Прямая в пространстве, различные виды уравнений.
- •21.Углы между плоскостями, прямыми, прямой и плоскостью.
- •22.Пересечение прямой и плоскости. Расстояние от точки до плоскости.
- •23.Расстояние от точки до прямой. Расстояние между прямыми в пространстве.
- •24.Эллипс; каноническое уравнение, исследование кривой.
- •25.Гипербола.
- •26.Параболла.
- •27.Функции двух переменных, область определения.
- •28.Линии уровня.
- •29.Частные производные функции двух переменных и их геометрический смысл.
- •30.Частные производные высших порядков. Теорема о равенстве смешанных производных.
- •31.Экстремумы функций двух переменных.
- •32.Первый полный дифференциал функции двух переменных и приближённые вычисления.
- •33.Частные производные сложной функции(3 случая).
- •34.Частные производные неявной функции.
- •35.Производная по направлению.
- •36.Градиент.
16.Скалярное произведение и его свойства.
Называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.
Скалярное
произведение векторов ![]() и
и ![]() будем
обозначать как
будем
обозначать как ![]() .
Тогда формула для вычисления
скалярного произведения имеет
вид
.
Тогда формула для вычисления
скалярного произведения имеет
вид 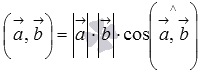 ,
где
,
где ![]() и
и ![]() -
1.свойство
коммутативности скалярного произведения
-
1.свойство
коммутативности скалярного произведения ![]() ;
;
свойство
2.дистрибутивности 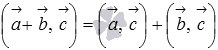 или
или 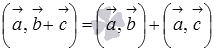 ;
;
3. сочетательное
свойство 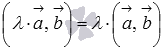 или
или 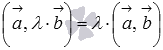 ,
где
,
где ![]() -
произвольное действительное число;
-
произвольное действительное число;
4.скалярный
квадрат вектора всегда не отрицателен 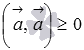 ,
причем
,
причем ![]() тогда
и только тогда, когда вектор
нулевой.
тогда
и только тогда, когда вектор
нулевой.
17.Векторное произведение и его свойства.
Векторным
произведением двух векторов ![]() и
и ![]() ,
заданных в прямоугольной системе
координат трехмерного пространства,
называется такой вектор
,
заданных в прямоугольной системе
координат трехмерного пространства,
называется такой вектор ![]() ,
что
,
что
он является нулевым, если векторы и коллинеарны;
он перпендикулярен
и вектору
и
вектору
(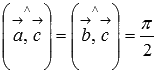 );
);
его длина
равна произведению длин векторов
и
на
синус угла между ними (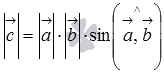 );
);
тройка
векторов ![]() ориентирована
так же, как и заданная система координат.
ориентирована
так же, как и заданная система координат.
1.Антикоммутативность 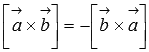 ;
;
2.Дистрибутивность  или
или 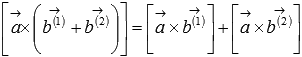 ;
;
3.Сочетательное
свойство 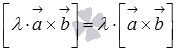 или
или 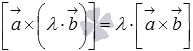 ,
где
,
где ![]() -
произвольное действительное число.
-
произвольное действительное число.
18.Смешанное произведение векторов.
Смешанным
произведением трех векторов ![]() и
и ![]() называется
действительное число, равное скалярному
произведению векторов
называется
действительное число, равное скалярному
произведению векторов  и
,
где
-
векторное произведение векторов
и
.
и
,
где
-
векторное произведение векторов
и
.
Из определения понятно, почему смешанное произведение часто называют векторно-скалярным произведением.
Смешанное
произведение векторов
и
обычно
обозначают ![]() .
В таких обозначениях по определению
смешанного произведения
.
В таких обозначениях по определению
смешанного произведения 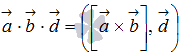 .
.
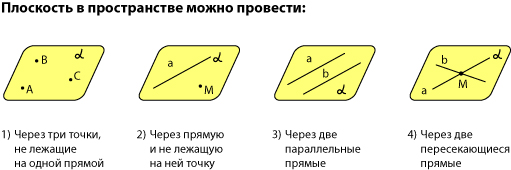
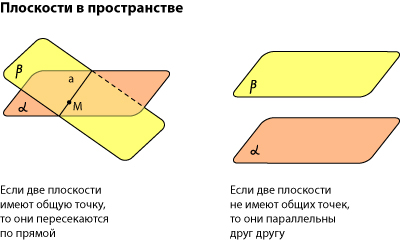
19.Плоскость в пространстве, различные виды уравнений.
Плоскость, прямая, точка — основные понятия геометрии. Нам трудно дать им четкие определения, однако интуитивно мы понимаем, что это такое. Плоскость имеет только два измерения. У нее нет глубины. Прямая имеет лишь одно измерение, а у точки вообще нет размеров — ни длины, ни ширины, ни высоты.
Плоскость бесконечна. Поэтому в задачах мы рисуем только часть плоскости. Надо же как-то ее изобразить.
 .
.
Уравнение ![]() называется общим
уравнением плоскости в
пространстве. Если не придавать
числам А, В, С и D конкретных
значений, то общее уравнение плоскости
называют уравнением
плоскости в общем виде.
называется общим
уравнением плоскости в
пространстве. Если не придавать
числам А, В, С и D конкретных
значений, то общее уравнение плоскости
называют уравнением
плоскости в общем виде.
Следует
заметить, что уравнение вида ![]() ,
где
,
где ![]() -
некоторое действительное число, отличное
от нуля, будет определять ту же самую
плоскость, так как равенства
и
эквивалентны.
К примеру, общие уравнения
плоскости
-
некоторое действительное число, отличное
от нуля, будет определять ту же самую
плоскость, так как равенства
и
эквивалентны.
К примеру, общие уравнения
плоскости ![]() и
и ![]() задают
одну и ту же плоскость, так как им
удовлетворяют координаты одних и тех
же точек трехмерного пространства.
задают
одну и ту же плоскость, так как им
удовлетворяют координаты одних и тех
же точек трехмерного пространства.
Например,
плоскость ![]() параллельна
оси абсцисс и перпендикулярна координатной
плоскости Oyz,
уравнение z = 0 определяет
координатную плоскость Oxy,
а общее уравнение плоскости
вида
параллельна
оси абсцисс и перпендикулярна координатной
плоскости Oyz,
уравнение z = 0 определяет
координатную плоскость Oxy,
а общее уравнение плоскости
вида ![]() соответствует
плоскости, проходящей через начало
координат.
соответствует
плоскости, проходящей через начало
координат.
Уравнение
плоскости вида ![]() ,
где a, b и c –
отличные от нуля действительные числа,
называется уравнением
плоскости в отрезках.
,
где a, b и c –
отличные от нуля действительные числа,
называется уравнением
плоскости в отрезках.
Для
примера построим в прямоугольной системе
координат Oxyz плоскость,
определенную уравнением плоскости в
отрезках 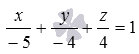 .
.
Общее
уравнение плоскости вида
называют нормальным
уравнением плоскости,
если длина
вектора ![]() равна
единице, то есть,
равна
единице, то есть, 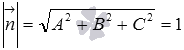 ,
и
,
и ![]() .
.
Часто
можно видеть, что нормальное уравнение
плоскости записывают в виде ![]() .
Здесь
.
Здесь ![]() -
направляющие косинусы нормального
вектора данной плоскости единичной
длины, то есть
-
направляющие косинусы нормального
вектора данной плоскости единичной
длины, то есть 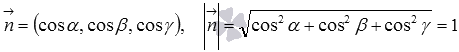 ,
а p –
неотрицательное число, равное расстоянию
от начала координат до плоскости.
,
а p –
неотрицательное число, равное расстоянию
от начала координат до плоскости.
Нормальное
уравнение плоскости в прямоугольной
системе координат Oxyz определяет
плоскость, которая удалена от начала
координат на расстояние p в
положительном направлении нормального
вектора этой плоскости ![]() .
Если p=0,
то плоскость проходит через начало
координат.
.
Если p=0,
то плоскость проходит через начало
координат.
Приведем пример нормального уравнения плоскости.
Пусть
плоскость задана в прямоугольной системе
координат Oxyz общим
уравнение плоскости вида 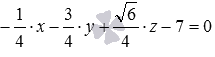 .
Это общее уравнение плоскости является
нормальным уравнением плоскости.
Действительно,
.
Это общее уравнение плоскости является
нормальным уравнением плоскости.
Действительно, ![]() и
нормальный вектор этой плоскости
и
нормальный вектор этой плоскости 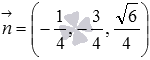 имеет
длину равную единице, так как
имеет
длину равную единице, так как 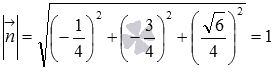 .
.
Построим плоскость Π, проходящую через т. М0, перпендикулярную вектору n (этот вектор называют нормальным вектором или нормалью плоскости). Утверждение
1: М М0М={x-x0, y-y0, z-z0} n A(x-x0)+B(y-y0)+C(z-z0)=0. |
Каноническое уравнение плоскости в пространстве: Аx+By+Cz+D=0, где D = -Ax0-By0-Cz0. |
