10.Решение слау методом Гаусса.

Смысл метода: последовательно исключаем переменную за переменной, пока в одной из строк не будет однозначно определена переменная x_i. Идею можно проиллюстрировать на простом примере: 

11.Решение слау методом обратной матрицы.

Составим алгоритм нахождения обратной матрицы с использованием равенства  .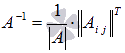

1.Вычисляем определитель матрицы А и убеждаемся, что он отличен от нуля (в противном случае матрица А необратима).

2.Строим   - матрицу из алгебраических дополнений элементов  .

3.Транспонируем матрицу  , тем самым получаем  .

4.Умножаем каждый элемент матрицы   на число  . Этой операцией завершается нахождение обратной матрицы  .

5.Проводим проверку результата, вычисляя произведения   и  . Если  , то обратная матрица найдена верно, в противном случае где-то была допущена ошибка.

12.Матрицы и действия с ними.

1. Сложение матриц - поэлементная операция

2. Вычитание матриц - поэлементная операция

3. Произведение матрицы на число - поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ij матрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

5. Возведение в степень

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A'

13.Ранг матрицы и способ его вычисления.

Итак, первым методом нахождения ранга матрицы является метод перебора миноров. Этот способ основан на определении ранга матрицы.

Пусть нам требуется найти ранг матрицы А порядка P * N.

Если есть хотя бы один элемент матрицы, отличный от нуля, то ранг матрицы как минимум равен единице (так как есть минор первого порядка, не равный нулю).

Далее перебираем миноры второго порядка. Если все миноры второго порядка равны нулю, то ранг матрицы равен единице. Если существует хотя бы один ненулевой минор второго порядка, то переходим к перебору миноров третьего порядка, а ранг матрицы как минимум равен двум.

Аналогично, если все миноры третьего порядка равны нулю, то ранг матрицы равен двум. Если существует хотя бы один минор третьего порядка, отличный от нуля, то ранг матрицы как минимум равен трем, а мы преступаем к перебору миноров четвертого порядка.

И так далее. Отметим, что ранг матрицы не может превышать наименьшего из чисел p и n.

14.Обратная матрица.

Матрица   называется обратной для матрицы  , определитель которой отличен от нуля  , если справедливы равенства  , где E – единичная матрица порядка n на n.

15.Векторы на плоскости и в пространстве. Операции над векторами. Модуль вектора.

Вектор – это направленный отрезок прямой.

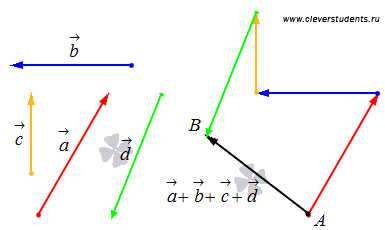
1.Сложение нескольких векторов на плоскости таким способом называется правилом многоугольника. Приведем иллюстрацию правила многоугольника.

2.Вычитание

Вектор -a называется противоположным вектору a, если их сумма равна нулевому вектору: (a + -a)=0. Противоположный вектор -a имеет длину |a| , коллинеарен и противоположно направлен вектору а. Нулевой вектор является противоположным самому себе.

-а

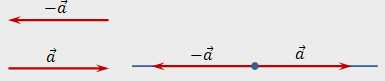
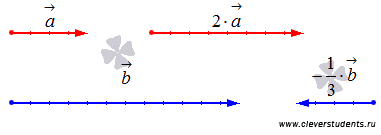
3.Умножение вектора на число

Умножение вектора на число k соответствует растяжению вектора в k раз при k > 1 или сжатию в K раз при 0 < k < 1, при k = 1 вектор остается прежним.К примеру, при умножении вектора a на число 2 нам следует вдвое увеличить его длину и сохранить направление, а при

умножении вектора b на минус одну треть следует уменьшить его длину втрое и изменить направление на противоположное.

Пусть   и   два произвольных вектора на плоскости или в пространстве. Отложим от некоторой точки O плоскости или пространства векторы   и  . Лучи OA и OBобразуют угол  .

Угол   называется углом между векторами   и  .

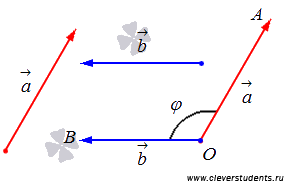
Угол между сонаправленными векторами равен нулю градусам (или нулю радиан), а угол между противоположно направленными векторами равен 180 градусам (или   радиан).

Два вектора называются перпендикулярными, если угол между ними равен 90градусам (или   радиан).

На этом обзор основных определений закончен.

Модуль вектора можно найти, если мы знаем его проекции на координатные оси.

на плоскости задан вектор а.

Опустим с начала и конца вектора перпендикуляры на координатные оси для нахождения его проекций. В соответствии с теоремой Пифагора

. Отсюда