7.Определители второго и третьего порядка, способы их вычисления.

Матрицей второго порядка называется таблица 

, (*)

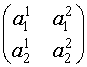составленная из элементов a₁¹, a₁², a₂¹, a₂².

Пары элементов a₁¹, a₁² и a₂¹, a₂² образуют строки матрицы, а пары a₁¹, a₂¹ и a₁², a₂² – столбцы.

Число (a₁¹·a₂² - a₁²·a₂¹), составленное из элементов матрицы (*), называют определителем второго порядка и обозначают 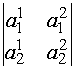 . Таким образом, чтобы сосчитать определитель второго порядка, надо перемножить элементы, стоящие на главной диагонали и вычесть произведение элементов, стоящих на побочной диагонали, например, определитель матрицы   равен  .

Матрицей третьего порядка называется таблица, составленная из девяти элементов 

:  .

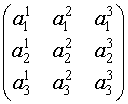Матрица, имеющая одинаковое число строк и столбцов, называется квадратной, а число ее строк (столбцов) называется порядком матрицы.

Говорят, что элементы a₁¹, a₂², a₃³ образуют главную диагональ, а a₁³, a₂², a₃¹ – побочную.

Определителем третьего порядка   называется число, равное сумме  . Это выражение называется разложением определителя по элементам первой строки.

8.Свойства определителей.

1.Определитель транспонированной( матрица, получающаяся из данной (прямоугольной или квадратной) матрицы А = II a_ik II после замены строк соответствующими столбцами) матрицы равен определителю исходной матрицы:

2.Умножение всех элементов строки или столбца определителя на некоторое число λ равносильно умножению определителя на это число:

.

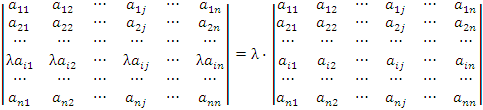3.Если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный.

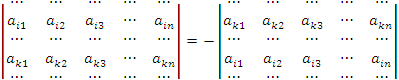
4.Если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю:

.

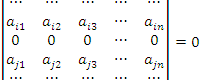5.Если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен нулю:

.

6.Если две строки (столбца) матрицы пропорциональны друг другу, то определитель этой матрицы равен нулю:

.

7.Определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали:

.

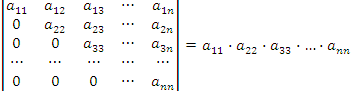8.Если все элементы k-ой строки (столбца) определителя представлены в виде сумм  a_k j + b_k j, то определитель можно представить в виде суммы соответствующих определителей:

  .

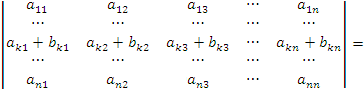
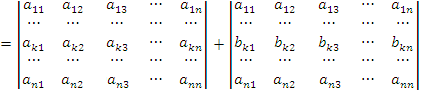9.Определитель не изменится, если к элементам любой его строки (или столбца) прибавить соответствующие элементы другой строки (или соответствующего столбца), умноженные на одно и то же число:

 

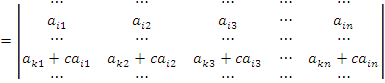
10.Пусть A и B – квадратные матрицы одного и того же порядка. Тогда определитель произведения матриц равен произведению определителей: 

9.Решение слау методом Крамера.

1.Вычисляем определитель основной матрицы системы  и убеждаемся, что он отличен от нуля.

2.Находим определители, которые являются определителями матриц, полученных из матрицы А заменой k-ого столбца (k = 1, 2, …, n) на столбец свободных членов.

Вычисляем искомые неизвестные переменные x₁, x₂, …, x_n по формулам  .

3.Выполняем проверку результатов, подставляя x₁, x₂, …, x_n в исходную СЛАУ. Все уравнения системы должны обратиться в тождества. Можно также вычислить произведение матриц A ⋅ X, если в результате получилась матрица, равная B, то решение системы найдено верно. В противном случае в ходе решения была допущена ошибка.