32.Первый полный дифференциал функции двух переменных и приближённые вычисления.

Определение.  Выражение   является главной частью полного приращения Δz и называется полным дифференциалом функцииz=f(x,у) и обозначается dz:       .                                                          (2)      Полагая в формуле (2) z равным х, найдем  , а при z=y  . Поэтому        .                                                           (3)      Из (1) следует, что  .      Функция f(x,y) называется дифференцируемой в точке (х,у), если она имеет в этой точке полный дифференциал.

33.Частные производные сложной функции(3 случая).

Пусть задана сложная функция  ,  ,   , тогда частные производные    можно найти по следующим формулам:

34.Частные производные неявной функции.

Неявной функцией  y  аргумента  x  называется функция, значения которой находятся из уравнения, связывающего  х,у и не разрешенного относительно  y, т.е.  

Производная неявной функции находится по следующей формуле:  .

Неявной функцией  z  аргументов  x  и  y  называется функция, значения которой находятся из уравнения, связывающего  z, x, y  и не разрешенного относительно  z, т.е.

Производные неявной функции находятся по следующим формулам: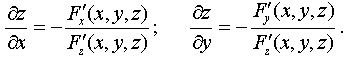

35.Производная по направлению.

Производной функции     в точке М(x, y)  в направлении вектора     называется  .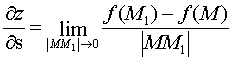

Если функция    дифференцируема, то производная в данном направлении вычисляется по формуле   , где  α  - угол между вектором  s  и осью  OX.

Пользуясь определением градиента, формуле для производной по направлению можно придать вид: 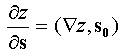 , где вектор  s_o  - орт вектора  s, т.е. производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления.

Производная    в направлении градиента имеет наибольшее значение, равное  .

36.Градиент.

Градиентом функции    в точке  M(x, y)  называется вектор с началом в точке  М, имеющий своими координатами частные производные функции  z,  . Для обозначения градиента часто используют символ  . Градиент указывает направление наибыстрейшего роста функции в данной точке.