1.Задача о вычислении площади криволинейной трапеции. Определённый интеграл.

Пусть функция y = f(x) непрерывна на отрезке [a; b] и не меняет знак на нем (неотрицательная или неположительная). Фигуру G, ограниченную линиями y = f(x), y = 0, x = a и x = b, называют криволинейной трапецией. Обозначим ее площадь S(G).

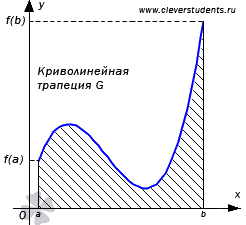Трапеция квадрируемая фигура. Если разбить отрезок [a; b] на n частей  точками   и обозначить  , а точки   выбирать так, чтобы   при  , то фигуры, соответствующие нижней и верхней суммам Дарбу, можно считать входящей P и объемлющей Q многоугольными фигурами для G.

Таким образом,   и при увеличении количества точек разбиения n, мы придем к неравенству  , где   - сколь угодно малое положительное число, а s и S – нижняя и верхняя суммы Дарбу для данного разбиения отрезка [a; b]. В другой записи  . Следовательно, обратившись к понятию определенного интеграла Дарбу, получаем  .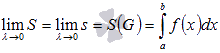

Последнее равенство означает, что определенный интеграл 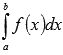  для непрерывной и неотрицательной функции y = f(x) представляет собой в геометрическом смысле площадь соответствующей криволинейной трапеции.

2.Теорема Лейбница. Связь неопределённого и определённого интеграла.

3.Определённое интегрирование по частям.

Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

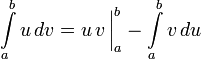
Предполагается, что нахождение интеграла   проще, чем  . В противном случае применение метода неоправданно.

4.Интегрирование подстановкой, замена пределов интегрирования.

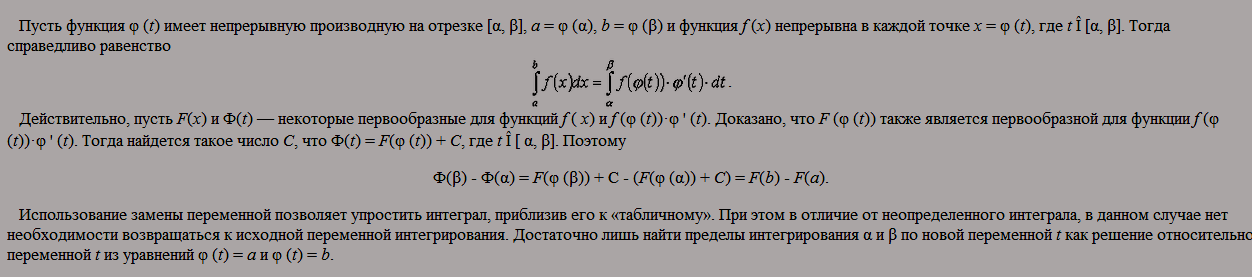
5.Свойства определённого интеграла.

1.В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:

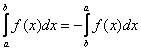
2.Линейность:  

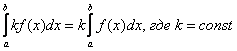
– это справедливо не только для двух, но и для любого количества функций.

3.Замену переменной интегрирования,

Пусть   является первообразной для   на отрезке   и пусть   — дифференцируемая функция на отрезке  , отображающая его в отрезок  , причем    . В предыдущем пункте мы видели, что

Значит,

В результате мы приходим к следующему утверждению: Пусть функция   имеет первообразную на отрезке  , а функция   определена на отрезке   и дифференцируема внутри этого отрезка, причем   и  . Тогда

(1) На этом утверждении и основан метод замены переменной под знаком определенного интеграла. Заметим, что на практике формула (1) используется как "слева направо", так и "справа налево".

Условие, что при   имеем:  , заведомо выполняется, если функция   монотонна на отрезке . Это имеет место, если ее производная сохраняет знак на  .

 4.Формула интегрирования по частям:

6.Приложения определённого интеграла (площадь фигуры, объём тела вращения).

Объём.

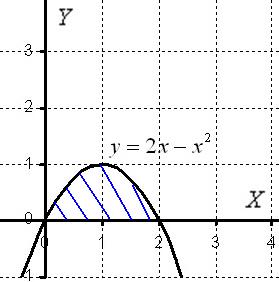
Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.

Плоская фигура ограничена графиком параболы   сверху. Это и есть та функция, которая подразумевается в формуле.

В практических заданиях плоская фигура иногда может располагаться и ниже оси  . Это ничего не меняет – подынтегральная функция в формуле возводится в квадрат:  , таким образом интеграл всегда неотрицателен.

Вычислим объем тела вращения, используя данную формулу:

есть площадь фигуры (определённый интеграл численно ей равен).

Просто возьмите интеграл от (2x-x^2) и вычтите из верхнего нижнее.