11.Решение слау методом обратной матрицы.

Запишем систему в матричной форме:  , где  

Решение системы найдем по формуле  

Обратную матрицу найдем по формуле: , где   – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров 

Двойной подстрочный индекс указывает, что элемент   находится в первой строке, третьем столбце, а, например, элемент   находится в 3 строке, 2 столбце

Таким образом:

– матрица миноров соответствующих элементов матрицы  .

 – матрица алгебраических дополнений.

 – транспонированная матрица алгебраических дополнений.

Повторюсь, выполненные шаги мы подробно разбирали на уроке.Теперь записываем обратную матрицу:

Ни в коем случае не вносим   в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.

Осталось провести матричное умножение.

Обратите внимание, что деление на 60 выполняется в последнюю очередь.  Ответ: 

12.Матрицы и действия над ними.

1.Сложение

2.Вычитание

3.Произведение матрицы на число

4. Умножение A*B матриц

5.Возведение в степень m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы

Строки и столбцы поменялись местами

13.Ранг матрицы.

. Так как матрица ненулевая, то ее ранг не меньше единицы.

Минор второго порядка 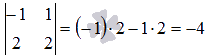  отличен от нуля, следовательно, ранг матрицы А не меньше двух. Переходим к перебору миноров третьего порядка. Всего их   штук.

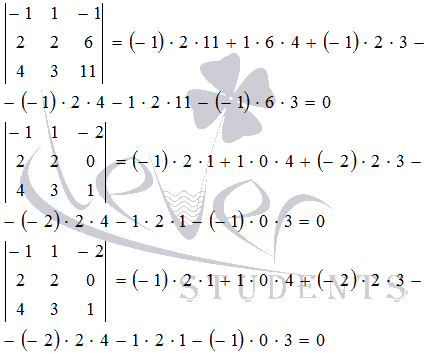
Все миноры третьего порядка равны нулю. Поэтому, ранг матрицы равен двум.

Ответ:

Rank(A) = 2.

14.Обратная матрица.

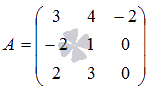. Найдите обратную матрицу.

Вычислим определитель матрицы А, разложив его по элементам третьего столбца:

Определитель отличен от нуля, так что матрица А обратима.

Найдем матрицу из алгебраических дополнений:

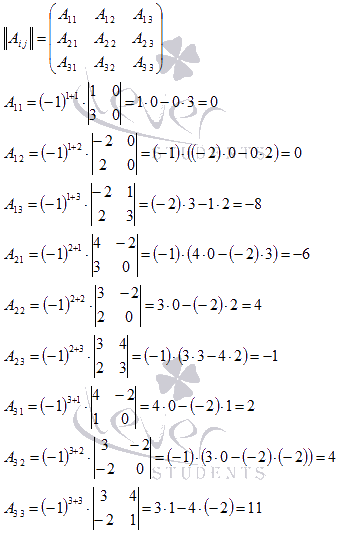
Поэтому

Выполним транспонирование матрицы из алгебраических дополнений:

Теперь находим обратную матрицу как  :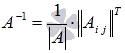

Проверяем полученный результат:

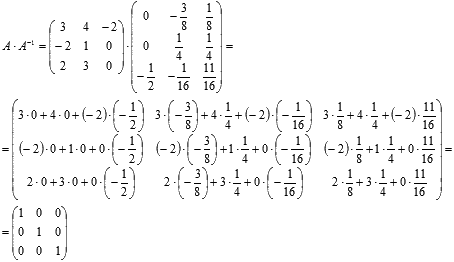
Равенства   выполняются, следовательно, обратная матрица найдена верно.

15.Векторы на плоскости и в пространстве. Операции над векторами. Модуль вектора.

Не имеет смысла приводить примеры, так как все разобрано в блоке теории.

16.Скалярное произведение и его свойства.

Вычислите скалярное произведение двух векторов   и  , если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.

17.Векторное произведение и его свойства.

Найдите длину векторного произведения векторов   и  , если известно  .

Мы знаем из определения, что длина векторного произведения векторов   и   равна произведению длин векторов   и   на синус угла между ними, поэтому,  .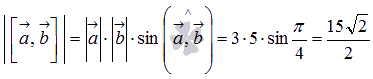

18.Смешанное произведение векторов.

Даны координаты трех векторов в прямоугольной системе координат  . Найдите смешанное произведение  .

Мы выяснили, что смешанное произведение векторов может быть вычислено через определитель матрицы третьего порядка, строками которой являются координаты векторов, то есть,

19.Плоскость в пространстве, различные виды уравнений.

Смысла не имеет, так как всё дано в разделе теории.

20.Прямая в пространстве, различные виды уравнений.

Составить канонические уравнения прямой по точке   и направляющему вектору 

Решение: Канонические уравнения прямой составим по формуле:

Ответ: 

Составить параметрические уравнения следующих прямых:

Решение: Прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.

а) Из уравнений   снимаем точку и направляющий вектор:  . Точку можно выбрать и другую (как это сделать – рассказано выше), но лучше взять самую очевидную. Кстати, во избежание ошибок, всегда подставляйте её координаты в уравнения.

Составим параметрические уравнения данной прямой:

Удобство параметрических уравнений состоит в том, что с их помощью очень легко находить другие точки прямой. Например, найдём точку  , координаты которой, скажем, соответствуют значению параметра  :

Таким образом: 

Нормальное:

Даны точка А(3,-1) и уравнение прямой   .

1)  Привести уравнение к нормальному виду, найти расстояние от точки до прямой.

2)  Составить уравнение прямой, проходящей через точку А параллельно данной прямой.

Решение. 1) Найдем нормирующий множитель   , m положительна, т. к.   . Нормируем уравнение

    ,

 где    a – угол между прямой и осью   ,    – расстояние от прямой до начала координат.

  – расстояние от точки А до прямой.

Найдем по таблице угол   . Уравнение можно записать

                               .

2) Прямая, параллельная данной, имеет тот же угловой коэффициент. По формуле (3) составим уравнение   , или в общем виде   . Вообще говоря, прямая, параллельная данной, будет иметь тот же нормальный вектор   , и её можно найти по формуле   , где    – координаты точки.

Ответ: нормальное уравнение прямой   , где   ;    – уравнение искомой параллельной прямой.

21.Углы между плоскостями, прямыми, прямой и плоскостью.

Вся нужная демонстрация в разделе теории.

22.Пересечение прямой и плоскости. Расстояние от точки до плоскости.

В разделе теории.

23.Расстояние от точки до прямой. Расстояние между прямыми в пространстве.

В разделе теории.

24,25,26,27,28 – в разделе теории.

29.Частные производные функции двух переменных и их геометрический смысл.

Найти частные производные первого и второго порядка функции 

Сначала найдем частные производные первого порядка. Их две.  или   – частная производная по «икс»  или   – частная производная по «игрек»

Начнем с  . Когда мы находим частную производную по «икс», то переменная  считается константой (постоянным числом).

(2) Используем правила дифференцирования  ,  .

(3) Используем табличные производные   и  .

(4) Упрощаем

Теперь  . Когда мы находим частную производную по «игрек», то переменная   считается константой (постоянным числом)

(1) Используем те же правила дифференцирования  ,  . В первом слагаемом выносим константу   за знак производной, во втором слагаемом ничего вынести нельзя поскольку   – уже константа.

(2) Используем таблицу производным элементарных функций. . То есть данная таблица равно справедлива и для  (да и вообще почти для любой буквы). В частности, используемые нами формулы выглядят так:   и  . Итак, частные производные первого порядка найдены. Шаг второй. Находим частные производные второго порядка. Их четыре.  или   – вторая производная по «икс»  или   – вторая производная по «игрек»  или   – смешанная производная «икс по игрек»  или   – смешанная производная «игрек по икс»

Для наглядности я перепишу уже найденные частные производные первого порядка:

Сначала найдем смешанные производные:

Как видите, всё просто: берем частную производную   и дифференцируем ее еще раз, но в данном случае – уже по «игрек».

Аналогично:

В практических примерах можно ориентироваться на следующее равенство:

Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.

Находим вторую производную по «икс». Никаких изобретений, берем   и дифференцируем её по «икс» еще раз:

Аналогично: