3.Определённое интегрирование по частям. =>Решаем.

Интегрируем по частям:

4.Интегрирование подстановкой, замена пределов интегрирования.

   Воспользуемся тригонометрической подстановкой  . Найдем пределы интегрирования   и   для новой переменной  .

Функция   возрастает на отрезке   и принимает на нем все значения от   до  . Поэтому   и   соответственно нижний и верхний пределы интегрирования для новой переменной  .

Функция   на отрезке   определена и дифференцируема внутри него, причем   и  . Значит, мы можем воспользоваться формулой (1). Используя решение примера 4, получаем:

5.Свойства определённого интеграла.

Со свойствами приведены примеры.

6.Приложения определённого интеграла (площадь фигуры, объём тела вращения).

Теория сопровождена примерами.

7.Определители второго и третьего порядка, способы их вычисления.

Теория сопровождена примерами.

8.Свойства определителей.

Теория сопровождена примерами

9.Решение СЛАУ методом Крамера.

  .

Основная матрица системы имеет вид  . Вычислим ее определитель по формуле  :

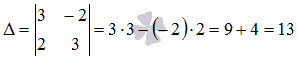
Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители   и  . Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель  . Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем .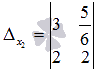

Вычисляем эти определители:

Находим неизвестные переменные x₁ и x₂ по формулам  :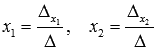

Выполним проверку. Подставим полученные значения x₁ и x₂ в исходную систему уравнений:

Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.

Ответ:

.

10.Решение слау методом Гаусса.

Элементарный пример:  x₁ - x₂ = 3  -x₁ + 2x₂ = 1  =========== (складываем строки)        -x₂ + 2x₂= 3 + 1 = 4 или x₂ = 4  Откуда, x₁ = 7.

Суть метода можно понять, проанализировав пример решения:

Запишем систему в виде расширенной матрицы:

2 -1 0 -1 1 4 1 2 3

0 13 14

Далее умножаем 2-ую строку на (2) и добавляем к первой:

0 1 8 -1 1 4 1 2 3

26 13 14

Добавим 3-ую строку к 2-ой:

0 1 8 0 3 7 1 2 3

26 27 14

Умножим первую строчку на (3), 2-ую строку умножаем на (-1). Следующее действие: складываем первую и вторую строки:

0 0 17 0 3 7 1 2 3

51 27 14

Теперь исходную систему можно записать как:  x₃ = 51/17  x₂ = [27 - 7x₃]/3  x₁ = [14 - (2x₂ + 3x₃)]  Из 1-ой строки выражаем x₃: 51/17 = 3  Из 2-ой строки выражаем x₂: (27 - 7*3)/3 = 2  Из 3-ой строки выражаем x₁: (14 - 2*2 - 3*3) = 1

Вывод: метод Гаусса является достаточно простым методом при небольшом количестве переменных и позволяет найти точное значение переменных. Процесс отыскания переменных можно упростить, если каждый раз сортировать столбцы по возрастанию.