Примеры разложения некоторых четных и нечетных функци в ряд Фурье.

Пример 1.

Разложить в ряд Фурье -периодическую функцию, которая на промежутке задана выражением .

Решение. Построим график функции (рис. 1.9).

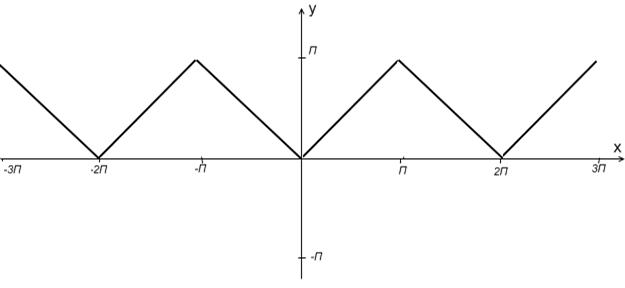
Рис.1.9. График функции к примеру 1

Функция четная, кусочно-монотонная, точек разрыва нет. Условия теоремы Дирихле 1.1 выполнены и как четная функция, она раскладывается в ряд (1.35)

в точках непрерывности, т. е. почти всюду

Пример 2.

Разложить в ряд Фурье -периодическую функцию, которая на промежутке задана выражением .

Решение. Построим график функции (рис. 1.10).

Рис. 1.10. График функции к примеру 2.

Функция нечетная, кусочно-монотонна на промежутке , имеет две точки разрыва 1-го рода : – периодическая функция.

Условия теоремы Дирихле 1.1 выполнены и так как функция нечетная, то ее ряд Фурье (1.41) в точках непрерывности почти всюду сходится к значениям функции:

Пример 3.

Пусть функция f (x) имеет период 2π и раскладывается в ряд Фурье:

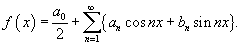
Вычислить коэффициенты a0, an и bn.

Решение.

Чтобы найти an, проинтегрируем ряд Фурье в интервале [−π, π]:

Для всех n > 0 справедливо

Поэтому, все члены в разложении Фурье справа от знака суммы равны нулю, что приводит к соотношению

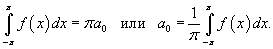
Чтобы определить коэффициенты an при m > 0, умножим обе части разложения в ряд Фурье на cos mx и проинтегрируем почленно:

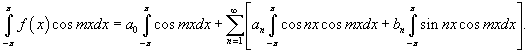
Первое слагаемое в правой части равно нулю. Тогда, используя тригонометрические тождества, можно записать

если m ≠ n.

В случае, если m = n, получаем

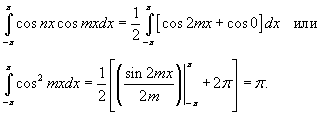
Таким образом,

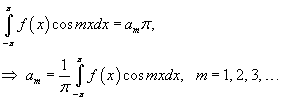
Аналогично, умножая ряд Фурье на sin mx и интегрируя почленно, получим выражение для bm:

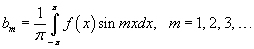
Переписывая формулы для an, bn, запишем окончательные выражения для коэффициентов Фурье:

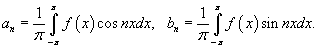
Пример 4.

Найти разложение в ряд Фурье прямоугольной функции с периодом 2π, определенной в интервале [−π, π]:

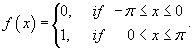
Вычислим сначала a0:

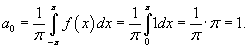
Определим теперь коэффициенты Фурье при n ≠ 0:

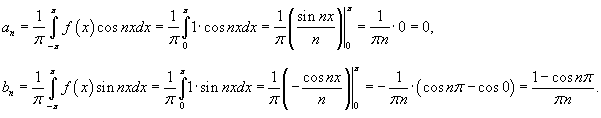
Поскольку , то можно записать

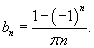
Таким образом, разложение в ряд Фурье для прямоугольной функции имеет вид

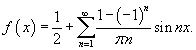
Можно легко вычислить несколько первых членов разложения. Полагая, например, n = 5, получаем

На рисунке 1 представлены график данной функции и ее аппроксимация рядом Фурье при n = 10.

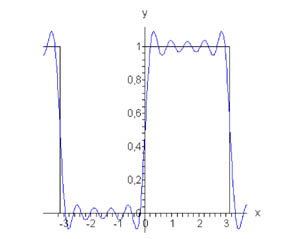
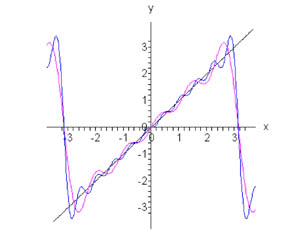
Рис.1, п=10 Рис.2, п=5, п=10

Пример 5.

Предположим, что f (x) является периодической функцией с периодом 2π. Пусть для . Найти разложение Фурье для заданной параболической функции.

Решение.

Так как функция четная, то коэффициенты bn = 0. Тогда

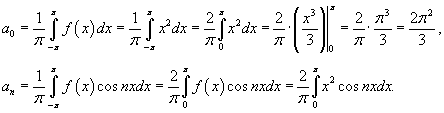
Применим дважды интегрирование по частям.

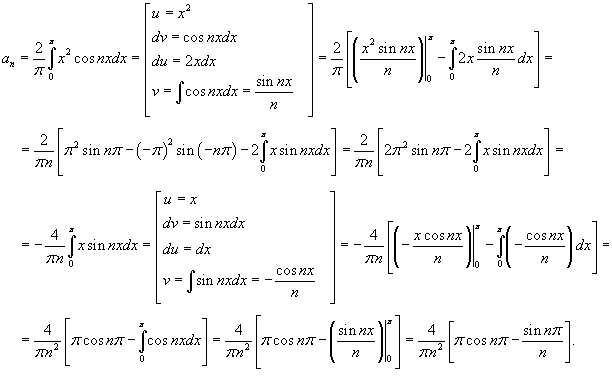
Поскольку и для натуральных n, то получаем

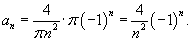
Тогда разложение параболической функции в ряд Фурье имеет вид (рисунок 3)

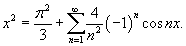
Рис.3, п=2, п=5 Рис.4, п=1, п=2