Министерство образования и науки Российской Федерации

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Математический факультет

Кафедра алгебры и математической кибернетики

Реферат Ряд Фурье. Разложение в ряд Фурье четных и нечетных функций.

ОГУ 220100.62.6012.069 Р

Руководитель

Старший преподаватель

_____________ Д.У. Шакирова

«___»____________20__г.

Исполнитель

Студент группы

11САУ(б)ИТ

_____________ Л.С. Арсланова

«___»____________20__г.

Оренбург 2012

Содержание

1 Ряды. Общие понятия…………………………………………………………..…3

2 Ряд Фурье. Общие понятия…………………………………………………….…5

3 Ряды Фурье для четных и нечетных функций……………………………….….7

4 Некоторые замечания разложения четных и нечетных функций в ряд Фурье.8

5 Примеры разложения некоторых четных и нечетных функци в ряд Фурье….11

Список использованных источников……………………………………………...19

1 Ряды. Общие понятия.

Рассмотрим числовую последовательность . Выражение

(1)

называется (бесконечным) числовым рядом, числа - членами ряда, - общим членом ряда, а сумма первых “n” членов - частичной суммой ряда.

Ряд называется сходящимся, если существует конечный предел последовательности частичных сумм , а число S называется суммой ряда.

Если последовательность не имеет конечного предела, то говорят, что ряд расходится. Однако в случае, когда , говорят, что ряд имеет бесконечную сумму.

Ряд

(2)

называется n-ым остатком ряда (1).

Свойства сходящихся числовых рядов.

1. Из сходимости ряда (1) следует сходимость ряда (2) и обратно.

2. Если сходится ряд (1) и а - некоторое действительное число, то сходится и ряд , и его сумма равна aS, т.е. справедливо равенство (здесь S - сумма ряда (1))

.

3. Если сходятся ряды (1) и

, (3)

имеющие, соответственно, суммы S и , то сходится и ряд , причём сумма его равна (S +).

4. Необходимое условие сходимости ряда.

Если ряд (1) сходится, то .

5. Ряд, составленный из элементов геометрической прогрессии

,

сходится при , причём , и расходится при . Его называют рядом бесконечной геометрической прогрессии.

2 Ряд Фурье. Общие понятия.

Идея о том, что любая периодическая функция может быть представлена в виде ряда гармонически связанных синусов и косинусов была предложена бароном Жан Батистом Жозефом Фурье (1768 − 1830).

Говорят, что функция f (x) имеет период P, если f (x + P) = f (x) для всех значений x. Пусть период функции f (x) равен 2π. В этом случае достаточно рассмотреть поведение функции в интервале [−π, π].

Предположим, что функция f (x) с периодом 2π абсолютно интегрируема в интервале [−π, π]. При этом является конечным так называемый интеграл Дирихле:

Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).

Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции (Смотрите об условиях сходимости также раздел Сходимость рядов Фурье).

Если x0 − точка разрыва, то ряд Фурье сходится к значению

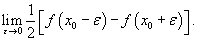
Ряд Фурье функции f (x) представляется в виде

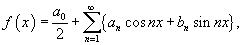
где коэффициенты Фурье a0, an и bn определяются формулами

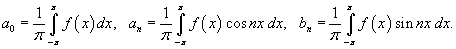
Иногда используются альтернативные формы записи для разложения в ряд Фурье. Заменяя an и bn новыми переменными dn и φn или dn и θn , где

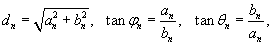
можно, соответственно, записать