1Определение предела функции основные теоремы предела

Основные теоремы о пределах

Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.

Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки  , за исключением, может быть, самой точки  , то либо они имеют один и тот же предел при  , либо обе не имеют предела в этой точке.

Теорема 2. Если функции f(x) и  g(x) имеют пределы в точке  , то:

1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.

         (3)

2) предел произведения функций равен произведению пределов сомножителей, т.е.

            (4)

3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.

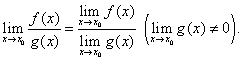           (5)

Замечание. Формулы (3) и (4) справедливы для любого конечного числа функций.

Следствие 1. Предел постоянной равен самой постоянной, т.е.

Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.

Пример 3. Найти предел:

Решение.

 

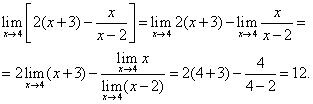
Пример 4. Найти предел:

Решение. Предварительно убедимся, что предел делителя не равен нулю:

Таким образом, формула (5) применима и, значит,

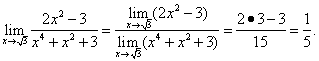
Теорема 3 (о пределе сложной функции). Если существует конечный предел

а функция f(u) непрерывна в точке  , то

Другими словами, для непрерывных функций символы предела и функции можно поменять местами.

Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.

2Два замечательных предела

Первый замечательный предел

Рассмотрим следующий предел:   (вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала).

Согласно нашему правилу нахождения пределов (см. статью Пределы. Примеры решений) пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида  , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:

 

Данный математический факт носит название Первого замечательного предела. Аналитическое доказательство предела приводить не буду, а вот его геометрический смысл рассмотрим на уроке о бесконечно малых функциях.

Нередко в практических  заданиях функции могут быть расположены по-другому, это ничего не меняет:

 – тот же самый первый замечательный предел.

! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде  , то и решать его нужно в таком же виде, ничего не переставляя.

На практике в качестве параметра   может выступать не только переменная  , но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.

Второй замечательный предел

В теории математического анализа доказано, что:

Данный факт носит название второго замечательного предела.

Справка:   – это иррациональное число.

В качестве параметра   может выступать не только переменная  , но и сложная функция.Важно лишь, чтобы она стремилась к бесконечности.

3Определение производной функции. Правила и формулы диффиринцирования

Производная постоянной величины.

Если f(x) = С, то

Доказательство этого правила рассмотрено на странице Определение производной.

Производная функции, умноженной на постоянную величину.

Пусть k некоторая константа. Если f(x) - дифференцируемая функция, то произведение kf(x) также дифференцируемо и

Производная суммы функций.

Пусть f(x) и g(x) являются дифференцируемыми функциями. Тогда сумма двух функций также дифференцируема и

Пусть n функций f₁(x), f₂(x),…, f_n(x) являются дифференцируемыми. Тогда их сумма также дифференцируема и

Из этого и предыдущего правил следует, что производная разности функций равна разности производных при условии дифференцируемости данных функций:

Можно сформулировать более общее правило: 

Производная линейной комбинации функций.

Предположим, что f(x) и g(x) являются дифференцируемыми функциями, а a и b - произвольными действительными числами. Тогда функция h(x) = af(x) + bg(x) также дифференцируема и

Добавим в данный список еще одно простое правило:

Производная функции y = x.

Если f(x) = x, то

Вывод этой формулы также приведен на странице Определение производной. 

4Монотонность и Экстремумы функций

2.6. Монотонность, экстремумы функции

Функция называется возрастающей если большему значению аргумента соответствует большее значение функции, а меньшему соответствует меньше.

Функция называется убывающей если большему значению аргумента соответствует меньшее значение функции, а меньшему соответствует большее.

Теорема. У возрастающей функции производная больше 0 ( ).

Доказательство:

 

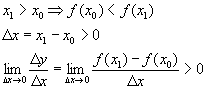
x		-1
y		min
	–	0	+

 

Экстремумы функции.

Т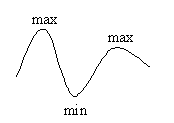 очка  -называется точкой max, если существует некоторая окрестность точки, что для любой точки x из этой окрестности  .

Точка  -называется точкой min, если существует некоторая окрестность точки, что для любой точки x из этой окрестности  .

Необходимый признак экстремума, если   -точка экстремума. 

 

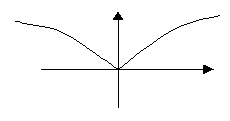
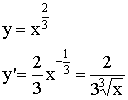
Если    и  , то это точка экстремума.

Если   - точка экстремума и существует  , то производная  =0. Точка, в которой производная, равна нулю, называется критической точкой.

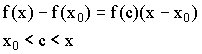 , теорема Логранжа. 

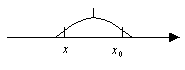
Первый достаточный признак экстремума.

Если при переходе через критическую точку производная меняет знак с ”+” на “-“,то в этой точке максимум.

Если при переходе через критическую точку производная меняет знак с ”-” на “+“,то в этой точке минимум.

 

Второй достаточный признак экстремума.

Если в критической точке 2-ая производная больше нуля, то это точка минимума, а если в критической точке 2-ая производная меньше нуля, то это точка максимума.

Пример:

   

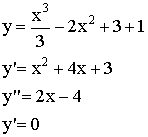
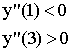
x		1		3
y		Max		Min
	+	0	-	0	+

5Неопределенный интеграл и его свойства

Определение первообразной и неопределенного интеграла

Функция F(x) называется первообразной функции f(x), если

Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функцииf(x) и обозначается как

Таким образом, если F - некоторая частная первообразная, то справедливо выражение

где С - произвольная постоянная. 

Свойства неопределенного интеграла

В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,  а, k, C - постоянные величины.









Таблица интегралов

В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показательной функции (b ≠ 1, b > 0).

6Площадь криволинейной трапеции

Площадь криволинейной трапеции, ограниченной сверху графиком функции y=f (x), снизу — осью Ох, слева и справа прямыми х=a, x=b, находят по формуле Ньютона-Лейбница (ф. Н-Л):

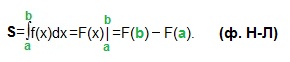
Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=4x-x²;y=0; x=0; x=4.

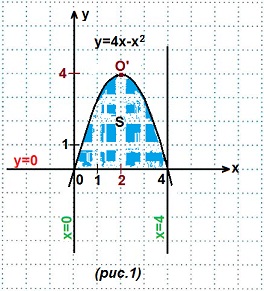
Решение.  Строим графики данных линий.  (рис. 1). 1) y=4x-x² — парабола (вида y=ax²+bx+c). Запишем данное уравнение в общем виде:y=-x²+4x. Ветви этой параболы направлены вниз, так как первый коэффициент а=-1<0.

Вершина параболы находится

в точке O′(m; n), где

О′(2; 4). Нули функции (точки пересечения графика с осью Ох) найдем из уравнения:

4х-х²=0.

Выносим х за скобки, получаем:  х(4-х)=0. Отсюда, х=0 или х=4.  Абсциссы точек найдены, ордината равна нулю — искомые точки: (0; 0) и (4; 0).

2) y=0 — это ось Ох; 3) х=0 — это ось Оy; 4) х=4 — прямая, параллельная оси Оy и отстоящая от нее на 4 единичных отрезка вправо.

Площадь построенной криволинейной трапеции находим по (ф. Н-Л). У нас f (x)=4x-x²,a=0, b=4.

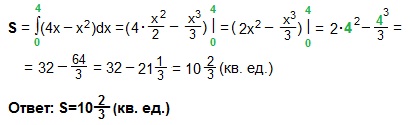
7Сочетание размещения и перестановки