
- •Постановка задач теорії керування.
- •2. Структурні схеми систем керування.
- •3. Коротка класифікація систем керування
- •4. Перехідна та імпульсна перехідна функції лінійних систем керування.
- •5.Зв’язок між вхідним і вихідним сигналами лінійної одновимірної системи керування
- •6.Перетворення Лапласа. Передавальна функція лінійної стаціонарної одновимірної системи керування
- •7. Функції від матриць. Подання розв’язку стаціон. І нестаціон. Лінійних систем керування через фундаментальний р – ок.
- •8.Подання розв’язку нестаціонарних лінійних систем керування через фундаментальний розв’язок
- •9.Поняття спряжених систем. Теорема про властивості розв’язків та фундаментальних матриць лінійних систем і спряжених систем Означення 6.1 Дві системи, які описуються рівняннями
- •10. Задача про керовність. Означення керовності.
- •11. Теорема про необхідні і достатні умови керовності.
- •12. Лема про ранг матриці керовності лін. Стаціон. С-ми
- •12. Лема про інваріантний підпростір лінійної стаціонарної системи .
- •15. Теорема про структуру лін. Стаціонарної системи.
- •16. Достатні умови керовності лінійної нестаціонарної системи.
- •17. Керовність систем з дискретним аргументом. Теорема про необхідні і достатні умови
- •18. Задача про спостережуваність систем з непевним аргументом
- •19. Необхідні і достатні умови спостережуваності системи з неперервним аргументом
- •20. Рівняння спостерігачів для систем з неперервним аргументом.
- •21. Спостережуваність систем з дискретним аргументом. Теорема про необхідні і достатні умови.
- •22. Рівняння спостерігачів для систем з дискретним аргументом.
- •23. Постановка задач оптимального керування
- •25. Принцип максимуму Гамільтона-Понтрягіна. Теорема (без доведення).
- •26.Алгоритм принципу максимуму.
- •27.Оптимальний регулятор лінійної системи керування (на основі принципу максимуму).
- •28. Диференціювання функціоналів на траєкторіях систем керування з дискретним аргументом.
- •31. Інтегральна форма рівнянь Беллмана
- •32. Інтегральна форма рівнянь Беллмана
- •33. Оптимальний регулятор на основі принципу оптимальності Беллмана
- •34. Алгоритм побудови адаптивного регулятора для систем керування з неперервним алгоритмом.
16. Достатні умови керовності лінійної нестаціонарної системи.
Розглянемо лінійну нестаціонарної систему
(1.1)
Означення: Система (1.1) наз. керовною на заданому відрізку [t0,t1], якщо існує функція керування
u(t) t є [t0,t1] така, що для будь-яких x0,x1 є Х розв’язок рівняння (1.1) x(t)= x(t,u(t))
задовольняє умови x(t0) = x0, x(t1)=x1 (1.2)
В подальшому вважатимемо, що елементи A і B мають відповідну кількість похідних (елементи A
і B гладкі функції). Позначимо z1(t)= B(t), тоді
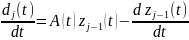 ,
j=2,3,…,n(1.3).
,
j=2,3,…,n(1.3).
Позначимо матрицю Z(t) = (z1(t), z2(t),…,zn(t)).
Теорема(достатні умови керовності (1.1) на [t0,t1]): Якщо rankZ(t)=n для деякого t, t є [t0,t1].(1.4),
то система (1.1) керовна на [t0,t1].
Доведення: Достатність. Потрібно показати, що за виконання (1.4) вектор-рядки матриці
w(t1, ) = X(t1, )B( ) (1.5) будуть лінійно незалежними Нехай виконується (1.4),
але не зважаючи на це вектор-рядки матриці (1.5) є лінійно-залежними.
Тобто
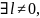 що
що
l*
w(t1,
)
= l*
X(t1,
)B(
)
= 0
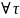 є [t0,t1].(1.6).
є [t0,t1].(1.6).
Запишемо співвідношення
l* X(t1, )B( ) = 0
l*
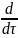 X(t1,
)B(
)
=
X(t1,
)B(
)
=
= l
*
( (A(
)B(
)
-
(A(
)B(
)
-
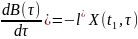 z2(
)
=0
z2(
)
=0
,
l*
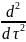 (X(t1,
)z2(
))
=
(X(t1,
)z2(
))
=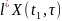 z3(
)
=0
z3(
)
=0
...................
l*
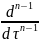 (X(t1,
)zn-1(
))
= (-1)n
zn(
)
=0
(X(t1,
)zn-1(
))
= (-1)n
zn(
)
=0
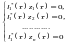 ,
,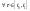 .
(1.7)
.
(1.7)
Тут l1( )=X*( t1, )l (1.8). Тоді l=( X*( t1, ))-1l1( )≠0,
є [t0,t1]. 0<||l||≤ || X*( t1, ))-1|| ||l1( )||.
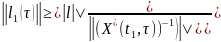 >0
(1.9).
>0
(1.9).
Ми одержали, що в (1.7) вектор l1( )≠0, є [t0,t1].
.Отже не справджується умова (1.3). Суперечність. Теорему доведено.
17. Керовність систем з дискретним аргументом. Теорема про необхідні і достатні умови
Розглянемо систему
виду (1.1),
(1.1),

 –
n-вимірний вектор,
–
n-вимірний вектор,
 –
m-вимірний вектор,
–
m-вимірний вектор,
 –
n*n ,
–
n*n ,
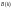 –
n*m;
–
n*m;
Означення.
Система (1.1) наз. керовною, якщо
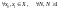 існує набір керування
існує набір керування
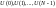 ,
що розв’язок системи (1.1) задовольняє
такі умови:
,
що розв’язок системи (1.1) задовольняє
такі умови:
 .
(1.2)
.
(1.2)
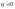 –
ціле число,
–
ціле число,
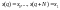 (1.2΄)
Означення.
Система (1.1) наз. керовною, якщо
,
будь-якого цілого числа
(1.2΄)
Означення.
Система (1.1) наз. керовною, якщо
,
будь-якого цілого числа
 існує
набір керування
існує
набір керування
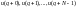 ,
що розв’язок системи (1.1) задовольняє
умови (1.2΄).
,
що розв’язок системи (1.1) задовольняє
умови (1.2΄).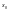 -
фіксований початковий момент.
Випишемо
позначення:
-
фіксований початковий момент.
Випишемо
позначення:




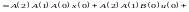
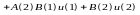 .
.
Позначимо
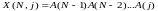 ,
(1.3)
,
(1.3)
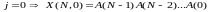 ,
(1.4)
,
(1.4)
 ,
(1.5)
,
(1.5)
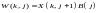 .
(1.6)
.
(1.6)
Отримаємо

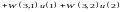 .
Якщо в останній рівності поставити
.
Якщо в останній рівності поставити
 ,
то можна записати у явному вигляді
,
то можна записати у явному вигляді
 .
.
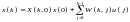 (1.7)
Запишемо
останнє рівняння так:
(1.7)
Запишемо
останнє рівняння так:
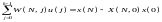 .
Задовольнимо умови (1.2):
.
Задовольнимо умови (1.2):
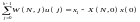 (1.8)
(1.8)
Теорема:
Достатність.
Для того щоб система (1.1) була керовною
н. і д. щоб виконувалась умова
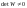 (1.9)
, де
(1.9)
, де
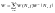 .
Доведення:
Нехай (1.9) справджується. Покажемо, що
(1.1) керована і побудуємо керування у
явному вигляді. Шукаємо керування у
вигляді
.
Доведення:
Нехай (1.9) справджується. Покажемо, що
(1.1) керована і побудуємо керування у
явному вигляді. Шукаємо керування у
вигляді
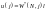 (1.10)
, де
(1.10)
, де
 –
деякий
–
деякий
 –
вимірний вектор. Підставляючи (1.10) у
(1.8) 0держимо
–
вимірний вектор. Підставляючи (1.10) у
(1.8) 0держимо
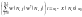 (1.11)
. Якщо справджується (1.9), то з (1.11) легко
знайти вектор
.
(1.11)
. Якщо справджується (1.9), то з (1.11) легко
знайти вектор
.
 ,
,
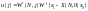 ,
,
 .
.
Необхідність.
(Від супротивного) Нехай (1.1) керована,
але
 –
особлива матриця, тобто
–
особлива матриця, тобто
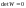 і (1.9) не виконується.
і (1.9) не виконується.
 –
-вимірний
вектор.
–
-вимірний
вектор.
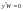 .
.
За припущенням
система (1.1) керована, тобто
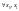 справджується рівність (1.8) при деяких
спеціально підібраних
справджується рівність (1.8) при деяких
спеціально підібраних
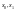 .
.
Виберемо
 ,
такими, щоб
,
такими, щоб
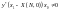 .
.
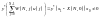 (1.12).
(1.12).
З іншого боку:
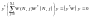
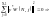
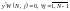 .
.
А це суперечить формулі (1.12). Припущення не вірне. Теорему доведено.
