8.Подання розв’язку нестаціонарних лінійних систем керування через фундаментальний розв’язок

Лінійна багатовимірна неперервна система керування описується рівнянням

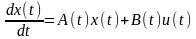. (5.1)

Використаємо відомі результати з теорії лінійних диференціальних рівнянь зі змінними коефіцієнтами. З цієї теорії нам відомо, що лінійно-незалежні розв’язки

( )

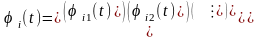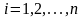однорідного рівняння

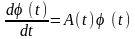(5.2)

утворюють фундаментальну матрицю

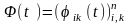. (5.3)

Фундаментальну матрицю можна знайти як розв’язок матричної задачі Коші

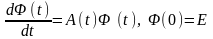. (5.4)

Для фундаментальної матриці існує обернена матриця 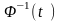в такому розумінні, що

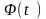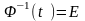= . (5.5)

Знайдемо розв’язок рівняння (5.1) за нульових початкових умов. Запропонуємо наступний алгоритм. Диференціюючи рівність (5.5), одержимо

.

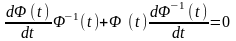Використовуючи (5.4), останнє співвідношення перепишемо так:

.

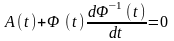Звідси

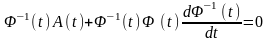
або

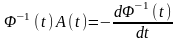. (5.6)

Співвідношення (5.6) помножимо на вектор , який задовольняє рівняння (5.1) за початкових умов 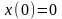. Тоді одержимо

.

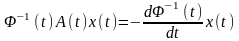Замість виразу 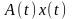підставимо його значення з рівняння (5.1). Тоді

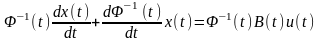
або

.

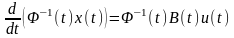Інтегруючи цю рівність в межах від 0 до , одержимо

.

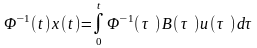Помножимо останню рівність на матрицю 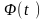. Тоді остаточно маємо

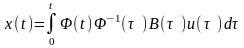. (5.7)

Зробивши позначення

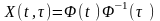(5.8)

рівність (5.7) запишемо у вигляді

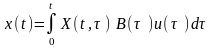. (5.9)

(5.10)

9.Поняття спряжених систем. Теорема про властивості розв’язків та фундаментальних матриць лінійних систем і спряжених систем Означення 6.1 Дві системи, які описуються рівняннями

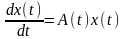(6.1)

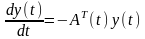, (6.2)

де 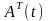– матриця транспонована до матриці 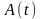, називаються спряженими.

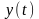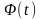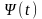Теорема 6.1 Нехай і – деякі розв’язки рівнянь (6.1) і (6.2); і – фундаментальні матриці цих рівнянь, тобто розв’язок задачі (5.4), а – розв’язок задачі

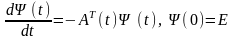. (6.3)

Тоді справджуються рівності

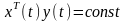; (6.4)

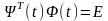. (6.5)

Доведення. Розглянемо вираз

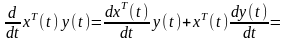
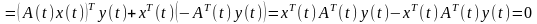
Тут використано означення транспонованої матриці. Отже рівність (6.4) доведена.

Рівність (6.5) доведемо аналогічно. Дійсно, те що добуток 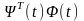сталий випливає з того, що

.

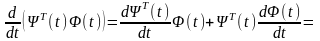
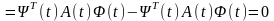Оскільки при цей добуток дорівнює 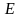(обидві матриці при одиничні), то рівність (6.5) справджуватиметься для всіх за теоремою існування і єдиності розв’язку однорідної системи диференціальних рівнянь.

З рівності (6.5) випливає, що

.

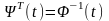Тому імпульсну перехідну матрицю (5.8) системи можна записати так:

.

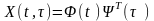З цієї причини спряжені системи грають важливу роль в теорії лінійних нестаціонарних систем.

10. Задача про керовність. Означення керовності.

Розглянемо лін. нестац.сист.керуван. (1.1.)

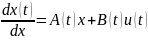
x(t) є Rⁿ – n-вимірний вектор u(t) є Rⁿ – m – вимірний вектор

A(t) –квадратна матриця A(t)=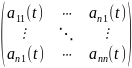

B(t)=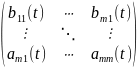

Вважаємо, що x(t) визнач.фазов. стан системи (1.1) і будемо говорити, що x(t) належ.фазовому простору Х, x(t) єХ.

Ф(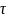 ) - норм.фундамент.матр.розв.лін. одн. системи, яка відновл.сист.(1.1)

Ф(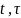 ) – розв.наступ.матр.задачі Коші

(1.3)

Позначимо w(t, ) матрицею імпульсних перехідних фнкцій для сист.(1.1)

w(t, )=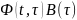 (1.4)

Розв.сист.(1.1), який задовол. початк. умову x(t₀) = х₀ можна записати у такому вигляді (1.5):

x(t)=Ф(t, t₀)x₀+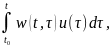 причому x(t₀) = х₀ (1.6)

Те, що x(t) є розв. (1.1), який задов. (1.6) легко перевырити. Для цього треба продиференц. ліву і праву част. (1.5) і підставити в (1.1)

Нехай сист. керув. описується такою системою 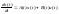(1) t₀<=t₁-моменти часу ; x - n-вимірний вектор; u – m-вимірний вектор ; A(t) – n x n, В(t) – n x m. A,B-неперервні, інтегровні (припускаєм)

Чи можна підібрати так u(t), щоб траекторія проходила через х₀,х₁?

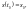
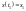Означ.: Система (1) називається цілком керовною , якщо для довільних t₀ , t₁ : t₀<t₁ ; x₀ x₁ : x₀ ,x₁єX знайдеться така ф-ція u(t) що розв-зок сист. (1) задов. умови: (2).