6.Перетворення Лапласа. Передавальна функція лінійної стаціонарної одновимірної системи керування

Основний зміст інтегральних перетворень, в тому числі й перетворення Лапласа, – це взаємно-однозначний перехід від одного класу функцій (функцій – класу оригіналів) до іншого класу функцій (наприклад, до , який називається класом зображень). У новому класі суттєво змінюється природа математичних операцій. А саме, інтегрування диференціального рівняння в класі оригіналів може звестися до відшукання коренів алгебраїчного рівняння в класі зображень. Такий перехід забезпечує спрощення відшукання розв’язку початкової задачі.

Означення 3.1 Оригіналом (за Лапласом) називається функція (нас цікавитимуть тільки дійсні функції) дійсного аргументу 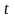, яка задовольняє умови:

1) – однозначна неперервна або кусково-неперервна функція разом зі своїми похідними до -го порядку на всій числовій осі ;

2) 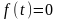при ;

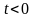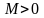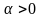3) існують такі числа і , що для

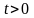
(точна нижня межа чисел називається показником росту функції ).

Означення 3.2 (зображення за Лапласом). Зображенням функції-оригінала називається функція комплексної змінної 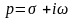, яка визначається за допомогою інтеграла Лапласа

. (3.1)

Наведемо без доведення наступні теореми.

Теорема 3.1 Якщо функція – оригінал з показником росту , то інтеграл збігається в півплощині 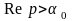, в цій півплощині інтеграл є аналітичною функцією і в цій області .

Теорема 3.2 Якщо функція аналітична в області , у цій області і інтеграл збігається, то функція є зображенням, а її оригінал можна знайти за формулою

, (3.2)

де інтегрування проводиться вздовж прямої, яка паралельна до уявної осі, на віддалі 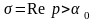від неї.

Розглянемо тепер лінійну систему керування зі сталими коефіцієнтами, яка описується рівнянням

(3.3)

і до моменту подачі сигналу керування ця система знаходиться в спокої, тобто

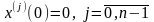, . (3.4)

Припустимо, що функції і задовольняють умови оригінала. Застосуємо до рівняння (3.3) перетворення Лапласа (3.1). Враховуючи умови (3.4), знайдемо

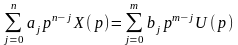, (3.5)

де

, .

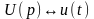Запровадимо позначення

, ,

. (3.6)

Тоді рівність (3.5) можна записати у вигляді

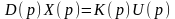,(3.7)

Або 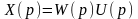. (3.8)

Функція називається передавальною функцією системи.

7. Функції від матриць. Подання розв’язку стаціон. І нестаціон. Лінійних систем керування через фундаментальний р – ок.

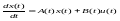(1)- нестац. лін.система x(t) є R , x є R u(t) є R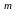 , , 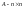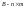– відомі.

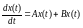(1.1)– стаціон. лін.система.

(2)

Лема: Ряд (2)збіг. абсолютно при кожному фікс. t для дов. квадратної матр. А з дійсними або комплексними елементами і рівномірно на будь-якому скінченому інтервалі.

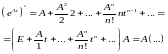
(3)

Теорема: Якщо матриця 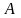задовольняє умови леми 4.1, то розв’язок матричної задачі Коші

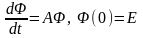(4)

має вигляд

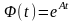(5)

Твердження1:

Розглянемо таку задачу

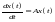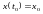(7), (8)

Розв’язком є вектор .

Теорема 4.3 Якщо матриця задовольняє умови леми 4.1, то розв’язок задачі

(9)

має вигляд

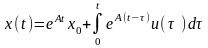. (10)

Доведення цієї теореми одержується безпосередньою перевіркою.

В рівності (10) покладемо всі компоненти вектора рівними нулеві, за винятком однієї 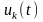( 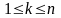), яку візьмемо рівною одиничному імпульсу , зосередженому в точці 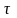. Позначимо розв’язок рівняння (0) за умови 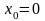. Одержимо

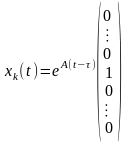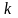– -й рядок.