
- •Постановка задач теорії керування.
- •2. Структурні схеми систем керування.
- •3. Коротка класифікація систем керування
- •4. Перехідна та імпульсна перехідна функції лінійних систем керування.
- •5.Зв’язок між вхідним і вихідним сигналами лінійної одновимірної системи керування
- •6.Перетворення Лапласа. Передавальна функція лінійної стаціонарної одновимірної системи керування
- •7. Функції від матриць. Подання розв’язку стаціон. І нестаціон. Лінійних систем керування через фундаментальний р – ок.
- •8.Подання розв’язку нестаціонарних лінійних систем керування через фундаментальний розв’язок
- •9.Поняття спряжених систем. Теорема про властивості розв’язків та фундаментальних матриць лінійних систем і спряжених систем Означення 6.1 Дві системи, які описуються рівняннями
- •10. Задача про керовність. Означення керовності.
- •11. Теорема про необхідні і достатні умови керовності.
- •12. Лема про ранг матриці керовності лін. Стаціон. С-ми
- •12. Лема про інваріантний підпростір лінійної стаціонарної системи .
- •15. Теорема про структуру лін. Стаціонарної системи.
- •16. Достатні умови керовності лінійної нестаціонарної системи.
- •17. Керовність систем з дискретним аргументом. Теорема про необхідні і достатні умови
- •18. Задача про спостережуваність систем з непевним аргументом
- •19. Необхідні і достатні умови спостережуваності системи з неперервним аргументом
- •20. Рівняння спостерігачів для систем з неперервним аргументом.
- •21. Спостережуваність систем з дискретним аргументом. Теорема про необхідні і достатні умови.
- •22. Рівняння спостерігачів для систем з дискретним аргументом.
- •23. Постановка задач оптимального керування
- •25. Принцип максимуму Гамільтона-Понтрягіна. Теорема (без доведення).
- •26.Алгоритм принципу максимуму.
- •27.Оптимальний регулятор лінійної системи керування (на основі принципу максимуму).
- •28. Диференціювання функціоналів на траєкторіях систем керування з дискретним аргументом.
- •31. Інтегральна форма рівнянь Беллмана
- •32. Інтегральна форма рівнянь Беллмана
- •33. Оптимальний регулятор на основі принципу оптимальності Беллмана
- •34. Алгоритм побудови адаптивного регулятора для систем керування з неперервним алгоритмом.
25. Принцип максимуму Гамільтона-Понтрягіна. Теорема (без доведення).
Розглянемо систему керування
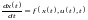 (1)
(1)
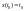 (2)
(2)
Критерій якості
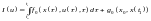 (3)
(3)
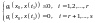 (4)
(4)
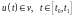 (5)
(5)
Розглянемо таку
оптимізовану задачу керування. Припустимо,
що в цих всіх співвідношеннях
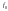 -
скалярна функція
-
скалярна функція
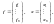
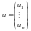 - керування
- керування
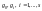 - скалярні функції
- скалярні функції
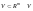 -
не залежить від
-
не залежить від
Треба знайти мінімум формула (3). Побудувати функцію Гамільтона для даної задачі:
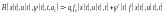 (6)
(6)
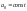
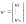
 (7)
(7)
Теорема. ( Принцип максимуму Гамільтона-Понтрягіна).
Нехай
 .
Мають другі частинні похідні, неперервні
за сукупністю змінних по своїх аргументах.
.
Мають другі частинні похідні, неперервні
за сукупністю змінних по своїх аргументах.
Функція
 Кусково
неперервна при
Кусково
неперервна при
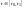 .
Нехай
.
Нехай
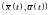 -
оптимальний розв’язок оптимальної
задачі, сформульованої вище.
-
оптимальний розв’язок оптимальної
задачі, сформульованої вище.
Тоді існують сталі
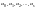 та
функції
та
функції
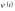 такі,
що
такі,
що
1)

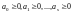
2) - розв’язок системи (7)
3) функція
 як
функція керування
при
фіксованому
як
функція керування
при
фіксованому
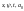 досягає в області
досягає в області
 свого
супремуму
свого
супремуму
 (8)
(8)
4)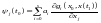 ,
,
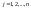 (9)
(9)
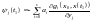 ,
(10)
,
(10)
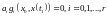 (11)
(11)
(9), (10) – умови трансверсальності,
(11) – умови доповнюючої нежорсткості
26.Алгоритм принципу максимуму.
Центральна
частина теореми це умова (8)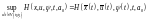 Для
оптимізаційної задачі будуємо функцію
Гамільтона. Якщо існує розв’язок
оптимізаційної задачі, то функція Н
визначена на непорожній множині своїх
аргументів.
Для
оптимізаційної задачі будуємо функцію
Гамільтона. Якщо існує розв’язок
оптимізаційної задачі, то функція Н
визначена на непорожній множині своїх
аргументів.
Зафіксуємо
 х,
х,
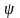 ,to
і знайдемо supH.
Це зробимо в усіх точках t
неперервності
функції U.
Якщо вдається знайти таку функцію U
і довести, що ця функція U
є єдиною, то ми можемо побудувати
оптимізаційний розв’язок задачі про
мінімізацію функціонала I(U)
(1)
(2)
,to
і знайдемо supH.
Це зробимо в усіх точках t
неперервності
функції U.
Якщо вдається знайти таку функцію U
і довести, що ця функція U
є єдиною, то ми можемо побудувати
оптимізаційний розв’язок задачі про
мінімізацію функціонала I(U)
(1)
(2)
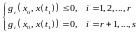 (4)
(4)
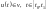 (5)
(5)
Нам
потрібно знайти
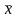 ,
а
,
а
1)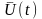 є
V,
t
є [t0,t1]-
знайшли вже
є
V,
t
є [t0,t1]-
знайшли вже
2)
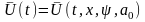
3)x(t), ,U0-?
Розглянемо систему
рівнянь
(1) – (7)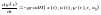 (7)
(7)
.
(2n
диференціальних рівнянь). Знайшовши
розв’язок він би залежав від 2n
довільних сталих. Для знаходження цих
сталих можна використати умови
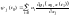 ,
(9)
,
(9)
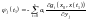 ,
(10)
,
(10)
. (їх є 2n) в цих умовах є ще S+1 стала (а0,…,аs)
2n-умов
9,
10. r-умов
(11)..
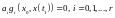 (11)
(11)
s-r-умов (друге співвідношення (4)
Отже є 2n+S умов. Ще потрібна одна умова. Функція Гамільтона є однорідною функцією параметрів і а.
H(x,
U,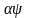 ,t,
,t,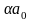 )=
)= (x,
U,
,t,a0)
(3.12)
(x,
U,
,t,a0)
(3.12)
Звернемося до умови (3.8).
Нехай >0. Тоді з умов (3.8)
U(t,
x,
,
)=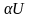 (t,
x,
,t,a0)
(t,
x,
,t,a0)
27.Оптимальний регулятор лінійної системи керування (на основі принципу максимуму).
Розглянемо лінійну систему керувань:
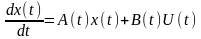 (4.1)
(4.1)
(4.2)
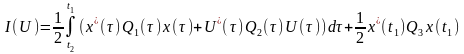 (4.3)
(4.3)
Немає ніяких обмежень.
Задача:
Знайти min:I(U)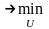 .Будуємо
функцію Гамільтона.
.Будуємо
функцію Гамільтона.
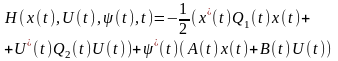
Вважаємо, що в 4.3 матриці Q1(t), Q2(t), Q3(t) є симетричними, при чому Q2(t) -додатно визначена.
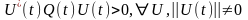
Тут
немає a0,
немає gi(x0,x(t1)),тому
ai=0,
Використаємо
умову (3.8). Знайдемо
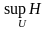 для
цього обчислимо gradUH(…)=0.
для
цього обчислимо gradUH(…)=0.

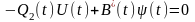 (4.4)
(4.4)
Ми знайшли в уявному вигляді:
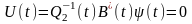 (4.5) t
є [t0,t1]
(4.5) t
є [t0,t1]
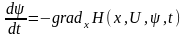
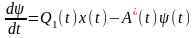 (4.6)
(4.6)
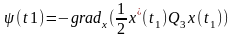
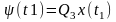 (4.7)
(4.7)
(4.2)
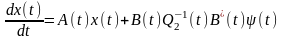 (4.8)
(4.8)
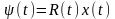 (4.9)
(4.9)
R(t)- невідома матриця
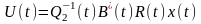

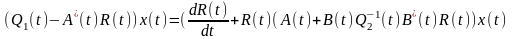 -
розв’язок задачі
-
розв’язок задачі
R(t1)x(t1)=-Q3x(t1)
28. Диференціювання функціоналів на траєкторіях систем керування з дискретним аргументом.
Розглянемо таку задачу.
Знайти мінімум функціонала
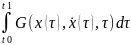 (2.1)
(2.1)
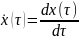
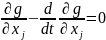 (2.2),
j=1,2,…n
(2.2),
j=1,2,…n
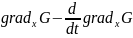 =0
(2.3)
=0
(2.3)
Нехай рівняння (1.1) таке, що дозволяє у явному вигляді знайти функцію u. Якщо цю функцію підставити у , то одержали б функціонал вигляду (2.1)
Розглянемо наступний критерій функціонування системи.
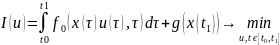 (2.4)
(2.4)
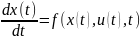 (2.5)
(2.5)
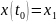 (2.6)
(2.6)
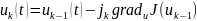 (2.7
)
(2.7
)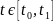
Щоб знайти похідну функціонала на траєкторії системи (2.5), введемо функцію
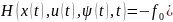 (2.8)
– функція Гамільтона
(2.8)
– функція Гамільтона
Покажемо,
що
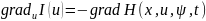 (2.9) на траєкторіях системи (2.3), а функція
(2.9) на траєкторіях системи (2.3), а функція
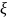 – це функція простір n, яка є розв’язком
диф. рівнянь
– це функція простір n, яка є розв’язком
диф. рівнянь
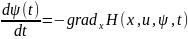 (2.10)
(2.10)
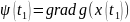 (2.11)
(2.11)
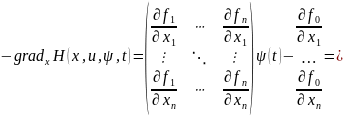
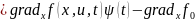
Покажемо,
що справджується (2.9) u(t)
~ x(t),t0,
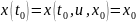
Надамо цьому параметру u деякого приросту u(t)+δu(t) ~ x(t) + δx(t) δu(t) – варіація керування, δx(t)- варіація розв’язку.
Нехай
ця траєкторія також виходить із точки
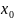 .
.
 |
|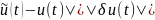
Розглянемо
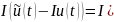 =
=
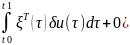 (2.12)
(2.12)
Якщо
приріст функціонала можна подати у
вигляді (2.12), то вектор
(t)=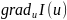
Покажемо,
що цей
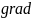 має
вигляд (2.9)
має
вигляд (2.9)
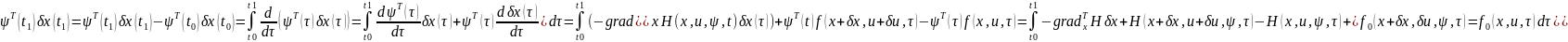
Нехай критерій якості функціонування системи керування має вигляд
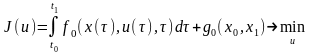 . (6.1)
. (6.1)
Математична модель системи керування задана у формі
,
,
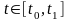 , (6.2)
, (6.2)
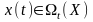 ,
, (6.3)
,
, (6.3)
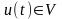 ,
.
(6.4)
,
.
(6.4)
Умови (6.3) визначають обмеження на фазові змінні, а (6.4) – обмеження на керування.
Задача оптимального керування:
знайти таке допустиме (кусково-неперервне
або обмежено вимірне) керування
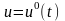 ,
,
щоб відповідна йому траєкторія
,
,
щоб відповідна йому траєкторія
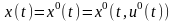 ,
,
,
,
задовольняла умову: функціонал
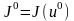 набуває мінімального значення або
значення своєї точної нижньої грані.
набуває мінімального значення або
значення своєї точної нижньої грані.
Пару функцій
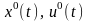 називатимемо розв’язком задачі
оптимального керування або оптимальним
розв’язком.
називатимемо розв’язком задачі
оптимального керування або оптимальним
розв’язком.
У наведеній постановці задачі оптимального
керування
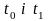 вважаються невідомими: вони залежать
від керування і поряд з ним їх потрібно
знайти. Таку задачу називають задачею
з вільним часом.
вважаються невідомими: вони залежать
від керування і поряд з ним їх потрібно
знайти. Таку задачу називають задачею
з вільним часом.
Якщо
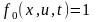 і
і
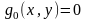 ,
то
,
то
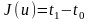 і задача (6.1)-(6.4) називається задачею про
швидкодію.
і задача (6.1)-(6.4) називається задачею про
швидкодію.
Принцип оптимальності Беллмана.
Якщо деяка траєкторія керованої системи
(6.2) з’єднує дві точки
та
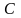 і є оптимальною траєкторією задачі
(6.1)-(6.4), то траєкторія, яка з’єднує точки
і є оптимальною траєкторією задачі
(6.1)-(6.4), то траєкторія, яка з’єднує точки
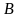 та
,
також буде оптимальною траєкторією при
будь-якому виборі точки
на оптимальній траєкторії
та
,
також буде оптимальною траєкторією при
будь-якому виборі точки
на оптимальній траєкторії
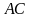 .
.
Друге формулювання принципу оптимальності
Беллмана. Нехай існує оптимальний
розв’язок
,
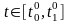 задачі (6.1)-(6.4) і нехай
задачі (6.1)-(6.4) і нехай
 довільний момент часу з проміжку
довільний момент часу з проміжку
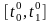 .
Тоді оптимальний розв’язок задачі
(6.1)-(6.4) при
.
Тоді оптимальний розв’язок задачі
(6.1)-(6.4) при
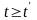 визначається значенням
визначається значенням
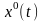 при
при
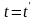 і не залежить від
і
і не залежить від
і
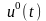 при
при
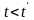 .
.
Третє формулювання принципу оптимальності
Беллмана. Оптимальний розв’язок
,
задачі (6.1)-(6.4) збігається при
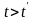 з оптимальним розв’язком задачі, яка
відрізняється від (6.1)-(6.4) лише тим, що
початковий момент зафіксований і
збігається з
,
а початкова точка фазової траєкторії
зафіксована і збігається з
з оптимальним розв’язком задачі, яка
відрізняється від (6.1)-(6.4) лише тим, що
початковий момент зафіксований і
збігається з
,
а початкова точка фазової траєкторії
зафіксована і збігається з
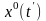 ,
тобто
,
тобто
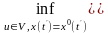 ,
(6.5)
,
(6.5)
де , – фіксовані.
