
- •Постановка задач теорії керування.
- •2. Структурні схеми систем керування.
- •3. Коротка класифікація систем керування
- •4. Перехідна та імпульсна перехідна функції лінійних систем керування.
- •5.Зв’язок між вхідним і вихідним сигналами лінійної одновимірної системи керування
- •6.Перетворення Лапласа. Передавальна функція лінійної стаціонарної одновимірної системи керування
- •7. Функції від матриць. Подання розв’язку стаціон. І нестаціон. Лінійних систем керування через фундаментальний р – ок.
- •8.Подання розв’язку нестаціонарних лінійних систем керування через фундаментальний розв’язок
- •9.Поняття спряжених систем. Теорема про властивості розв’язків та фундаментальних матриць лінійних систем і спряжених систем Означення 6.1 Дві системи, які описуються рівняннями
- •10. Задача про керовність. Означення керовності.
- •11. Теорема про необхідні і достатні умови керовності.
- •12. Лема про ранг матриці керовності лін. Стаціон. С-ми
- •12. Лема про інваріантний підпростір лінійної стаціонарної системи .
- •15. Теорема про структуру лін. Стаціонарної системи.
- •16. Достатні умови керовності лінійної нестаціонарної системи.
- •17. Керовність систем з дискретним аргументом. Теорема про необхідні і достатні умови
- •18. Задача про спостережуваність систем з непевним аргументом
- •19. Необхідні і достатні умови спостережуваності системи з неперервним аргументом
- •20. Рівняння спостерігачів для систем з неперервним аргументом.
- •21. Спостережуваність систем з дискретним аргументом. Теорема про необхідні і достатні умови.
- •22. Рівняння спостерігачів для систем з дискретним аргументом.
- •23. Постановка задач оптимального керування
- •25. Принцип максимуму Гамільтона-Понтрягіна. Теорема (без доведення).
- •26.Алгоритм принципу максимуму.
- •27.Оптимальний регулятор лінійної системи керування (на основі принципу максимуму).
- •28. Диференціювання функціоналів на траєкторіях систем керування з дискретним аргументом.
- •31. Інтегральна форма рівнянь Беллмана
- •32. Інтегральна форма рівнянь Беллмана
- •33. Оптимальний регулятор на основі принципу оптимальності Беллмана
- •34. Алгоритм побудови адаптивного регулятора для систем керування з неперервним алгоритмом.
Постановка задач теорії керування.
Приклад 1.
Нехай задана матер.точка маси m і відомо, що вона може здійснювати рух вздовж прямої під дією сили u.
Припустимо, що сила u задовольняє таку систему |u(t)|≤ u0 u0>0 (1.1)
d2x/dt2 = mu(t) (1.2) (прискорення точки пропорційне сумі сил, які діють на цю точку)
Для визначення руху цієї точки введемо такі позначення x1(t)=x(t), x2(t) = dx(t)/dt – фазові координати (1.3)
dx1 (t)/dt = x2(t),
dx2 (t)/dt= mu(t) (1.4)
x(t0) = x0,
x(t1) = x1, (1.5) – умови
d(x(t0))/dt = 0,
d(x(t1))/dt= 0 (1.6)
Знайти такий закон руху рівняння (1.2) x(t) матер.точки під дією сили u і при цьому виконуються умови (1.5) і (1.6). Тобто треба знайти таку силу u(t), яка забезпечила б переведення матер. Точки зі стану А= (х0,0) у стан В=(х0,0) за відрізок часу (t0,t1)
Початкові умови:
х1(t0) = x0, x2(t0) = 0 (1.7)
х1(t1) = x1, x2(t1) = 0
Для задачі (1.4)-(1.7) запровадимо такий критерій якості: підібрати силу u так для системи (1.4), яка забезпечить виконання умов (1.7) за оптимальний час
Приклад 2. (задача навігації)
Нехай корабель рухається по поверхні води, при цьому виконуються такі умови: курс корабля визначається кутом ψ. Знайти ψ так, щоб корабель з початкової точки А попав в точку В за мін.час за таких умов: швидкість |v| = 1 і течія води має швидкість S, напрямлена вздовж осі ох1
Побудуємо мат.модель:
dx1 (t)/dt = cos ψ +s
dx2 (t)/dt= sin ψ (1.9)
x(t0) = x0 1
x(t1) = x1 1, (1.10) – початкові та кінцеві умови
x(t0) = x1 2,
x(t1) = x2 2,
t0 – t1 -> min ψ (1.11)
cos 2ψ + sin2 ψ =1 (1.12) cos ψ = u1(t), sin ψ = u2(t)
dx1 (t)/dt = u1(t) +s
dx2 (t)/dt= u2(t) { u1(t) , u2(t): u1 2(t) + u2 2(t)=1, [t0,t1] }
Приклад 3. (задача переслідування)
|х з рискою(t) – x(t)| -> min
Sqrt ((x1 з рискою – x1)2 +( x2 з рискою – x2)2)
Припустимо, що є система, яка змінює свій стан в дискретний момент часу t. Припустимо, що в кожній з цих дискретних моментів система моде знаходитися в 4 станах : х(1), х(2), х(3), х(4).
х(і+1)>f(x(i), u(i))
Опишемо ф-цію f таблично
|
x(1) |
x(2) |
x(3) |
x(4) |
u(0) |
x(1) |
x(1) |
x(1) |
x(2) |
u(1) |
x(3) |
x(4) |
x(4) |
x(3) |
Нехай треба мінімізувати деяку функцію і яка залежить від кінцевого стану.
φ(х(n)) задамо таблицею
x(n) |
x(1) |
x(2) |
x(3) |
x(4) |
φ(х(n)) |
-2 |
3 |
-1 |
2 |
Нехай система дискретна аргументу починає функціонувати з деякого стану х(0), яке належить множині { х(1), х(2), х(3), х(4)}
Знайти керування u(0),u(1), u(2), u(3),…u(n-1) так, щоб ф-ція φ(х(n)) досягла мінімального значення.
2. Структурні схеми систем керування.
Будь-яку
сист керув можна подати таким чином
![]() .
А – обєкт керув, В – пристрій, який керує
обєктом А. Стан А визначаєтся деякою
кількістю n
чисел
.
А – обєкт керув, В – пристрій, який керує
обєктом А. Стан А визначаєтся деякою
кількістю n
чисел
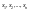 ,
які назив фазовими коорд обєкта. Для
скороч запису часто використ вектор
,
які назив фазовими коорд обєкта. Для
скороч запису часто використ вектор
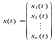 в n-вимірному
просторі, при кожному t.
Вектор x
назив вихідним сигналом системи або
фазовим станом системи, а простір Х –
фазовим простором. Стан обєкта А
змінюється під дією вхідних сигналів
в n-вимірному
просторі, при кожному t.
Вектор x
назив вихідним сигналом системи або
фазовим станом системи, а простір Х –
фазовим простором. Стан обєкта А
змінюється під дією вхідних сигналів
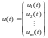 .
В намагається виробити такий сигнал
u(t),
щоб можна було б забезпечити певний
закон зміни вектора x(t).
x(t)=L(u(t)),
де L-деякий
оператор, який відображає структуру
обєкта А. Система керув набуває такого
вигляду
.
В намагається виробити такий сигнал
u(t),
щоб можна було б забезпечити певний
закон зміни вектора x(t).
x(t)=L(u(t)),
де L-деякий
оператор, який відображає структуру
обєкта А. Система керув набуває такого
вигляду
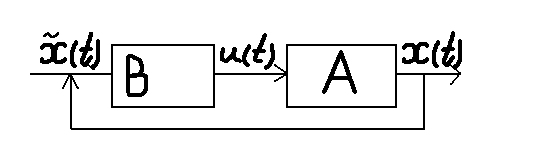 .
Вектор х вимірюється
і подається на ПК обєкту В по лініях
оберненого звязку. Знаючи поточний стан
обєкта х, ПК В виробляє деякі керування
u(t).
На вхід ПК В подається
.
Вектор х вимірюється
і подається на ПК обєкту В по лініях
оберненого звязку. Знаючи поточний стан
обєкта х, ПК В виробляє деякі керування
u(t).
На вхід ПК В подається
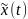 - це той бажаний режим, на який треба
вивести обєкт А,||x(t)-
||2.
Сист з оберненим звязком назив замкненими
сист керув.
- це той бажаний режим, на який треба
вивести обєкт А,||x(t)-
||2.
Сист з оберненим звязком назив замкненими
сист керув.
 ,
z(t)
– випадкові збурення, які діють на обєкт
керування. Тоді x(t)=x(
t,
z(t),
u(t)
), L(
x(t),
u(t),
z(t),
t
)=0. Вважатимемо, що L
таке рівняння
,
z(t)
– випадкові збурення, які діють на обєкт
керування. Тоді x(t)=x(
t,
z(t),
u(t)
), L(
x(t),
u(t),
z(t),
t
)=0. Вважатимемо, що L
таке рівняння
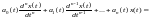
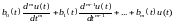 .
.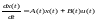 ,
де
,
де
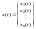 ,
,
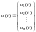 ,
A(t)
– матр
,
A(t)
– матр
 ,
B(t)
– матр
,
B(t)
– матр

