17) Индуктивность в цепи переменного тока

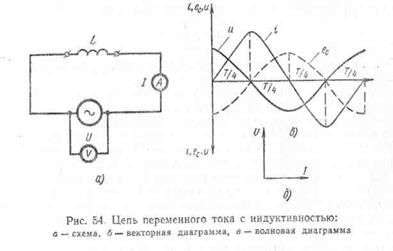
Прохождение электрического тока по проводнику или катушки сопровождается появлением магнитного поля. Рассмотрим электрическую цепь переменного тока (рис. 54,а), в которую включена катушка индуктивности, имеющая небольшое количество витком проволоки сравнительно большого сечения, активное сопротивления которой можно считать практически равным нулю

Под действием э.д. с. генератора в цепи протекает переменный ток, возбуждающий переменный магнитный поток. Этот поток пересекает «собственные» витки катушки и в ней возникает электродвижущая сила самоиндукции

где L — индуктивность катушки

скорость изменения тока в ней

Электродвижущая сила самоиндукции, согласно правилу Лен­ца, всегда противодействует причине, вызывающей ее. Так как э. д. с. самоиндукции всегда противодействует изменениям переменного тока, вызываемым э.д.с. генератора, то она препятствует прохож­дению переменного тока. При расчетах это учитывается по индук­тивному  сопротивлению,  которое  обозначается Х_L  и  измеряется

в омах. Таким образом, индуктивное сопротивление катушки Х_L зависит от величины э. д. с. самоиндукции, а следовательно, оно, как и э.д. с. самоиндукции, зависит от скорости изменения тока в ка­тушке (от частоты со) и от индуктивности катушки L

где X_L, — индуктивное сопротивление, ом

ώ — угловая частота переменного тока, рад/сек

L — индуктивность катушки, гн

Так как угловая частота переменного тока    , то индуктив­ное сопротивление

где, f—-частота переменного тока, гц

18) Емкость в цепи переменного тока

 

Положим, что участок цепи содержит конденсатор ёмкости С, причем сопротивлением и индуктивностью можно пренебречь. Обозначим разность потенциалов точек а и b через   и будем считать заряд конденсатора q и силу тока   положительными, если они соответствуют (рис. 10.4). Тогда  . Но  , следовательно, и

.

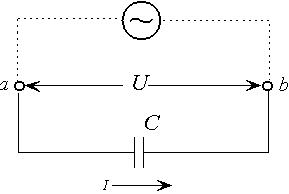
Рис. 10.4. Конденсатор в цепи переменного тока

Если сила тока в цепи изменяется по закону:

,             

 то

.

Постоянная интегрирования   здесь обозначает произвольный постоянный заряд конденсатора, не связанный с колебаниями тока и поэтому мы положим  . Следовательно,

 .

Сравнивая (10.1) и (10.2) мы видим, что при синусоидальных колебаниях тока в цепи напряжение на конденсаторе изменяется также по закону синуса, однако колебания напряжения на конденсаторе отстают по фазе от колебаний тока на  . Изменение тока и напряжения во времени изображено графически (рис. 10.5).

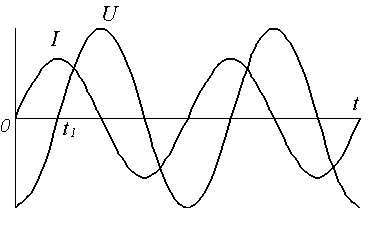
Рис. 10.5. Колебания тока в цепи и напряжения на конденсаторе

Полученный результат имеет простой физический смысл. Напряжение на конденсаторе в какой-либо момент времени определяется существующим зарядом конденсатора. Но этот заряд был образован током, протекавшим предварительно в более ранней стадии колебаний. Поэтому и колебания напряжения запаздывают относительно колебаний тока. Так, например, когда в момент времени   сила тока равна нулю (рис. 10.5), то на конденсаторе еще имеется отрицательный заряд, перенесенный током в предыдущий период времени, и напряжение не равно нулю. Для обращения в нуль этого заряда нужно, чтобы некоторое время   проходил ток положительного направления, и поэтому, когда заряд конденсатора станет равным нулю, сила тока уже не будет равна нулю.

Формула (10.2) показывает, что амплитуда напряжения на конденсаторе равна

.

Сравнивая это выражение с законом Ома для участка цепи с постоянным током ( ), мы видим, что величина

                                                                                                            (10.3)

играет роль сопротивления участка цепи. Потому она получила название сопротивления  ёмкости.

Полученные результаты можно представить в виде векторной диаграммы (рис. 10.6). Здесь вектор, изображающий колебания напряжения, уже не совпадает с осью токов. Он повернут в отрицательном направлении (по часовой стрелке) на угол  . Длина этого вектора равна амплитуде напряжения:  .

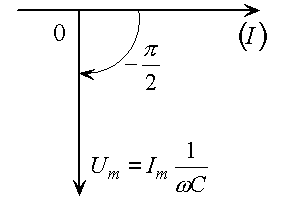
Рис. 10.6. Векторная диаграмма напряжения на конденсаторе

Из формулы (10.3) видно, что сопротивление емкости   зависит также от частоты  . Поэтому при очень высоких частотах, даже малые емкости могут представлять совсем небольшое сопротивление для переменного тока.

 

 

19) ЗАКОНЫ КИРХГОФА В ВЕКТОРНОЙ ФОРМЕ Анализ и расчет сложных цепей переменного тока, так же как и цепей постоянного тока, производятся с помощью уравнений электрического состояния, составленных по законам Кирхгофа. Для цепей переменного тока вомногих случаях целесообразнее записывать уравнения электрического состояния цепей по законам Кирхгофа в векторной форме. На основании уравнений, записанных в векторной форме, легко построить векторную диаграмму. Согласно первому закону Кирхгофа сумма токов в узле равна нулю при любом законе изменения токов во времени Σi = 0. Для замкнутого контура электрической цепи может быть записано уравнение по второму закону Кирхгофа, связывающее мгновенные значения ЭДС, токов и напряжений независимо от того, по какому закону изменяются эти величины: Σe = Σir + Σu. В цепях синусоидальных ЭДС ток и напряжение изменяются синусоидально, поэтому они могут быть представлены вращающимися векторами и законы Кирхгофа записаны в векторной форме. Первый закон: Геометрическая сумма токов узла равна нулю: ΣĪ = 0. Второй закон: Геометрическая сумма ЭДС при обходе по замкнутому контуру равна геометрической сумме произведений токов на полные сопротивления соответствующих ветвей контура плюс геометрическая сумма напряжений, действующих в контуре: ΣĒ = ΣIZ + ΣŪ = ΣIr + ΣIX + ΣŪ. Знаки перед соответствующими членами уравнения определяются так же, как и для цепей постоянного тока: при совпадении направлений E, I, U снаправлением обхода контура перед соответствующим членом уравнения проставляется знак плюс, при несовпадении — знак минус.

20)

МОЩНОСТЬ ПЕРЕМЕННОГО ТОКА

Мощность, выделяемая в цепи переменного тока, непрерывно изменяется. Однако, если разбить период переменного тока и напряжения на очень малые интервалы времени, то в течение их можно считать значения тока и напряжения неизменными. Энергия, выделяемая за малый интервал времени  , равна произведению средних значений тока и напряжения на этот интервал:

В общем случае ток и напряжение в цепи могут быть сдвинуты друг относительно друга по фазе на некоторый угол   (рис. 2-14, а).

Рис. 2-14. Мощность переменного тока. а - ток и напряжение сдвинуты по фазе на угол  ; б - ток и напряжение сдвинуты по фазе на 90°.

Если момент перехода напряжения через нуль к положительным значениям принять за начало отсчета времени, то в начальный момент времени

Энергия, выделяемая в цепи за малый интервал времени  ,

Пользуясь тригонометрической формулой

получим:

Энергия, выделяемая за полный период переменного тока, является суммой энергий, выделяемых за все малые интервалы времени в течение этого периода:

(2-21)

Поскольку в первом слагаемом первые три сомножителя - постоянные величины, а во втором слагаемом суммирование произведения за период дает нуль (так как косинус половину периода имеет положительные, а половину периода такие же отрицательные значения), то

Средняя активная мощность переменного тока за период

(2-22)

Если ток и напряжение совпадают по фазе, что бывает при прохождении тока через активное сопротивление, то

Последнее выражение показывает, что в цепи переменного тока выделяется такая же активная мощность, которую выделял бы постоянный ток при его величине и величине напряжения, в   раз меньших амплитуды переменного тока и напряжения. Эти величины называютдействующими (или эффективными) значениями переменного тока I и напряжения U:

Поскольку в рассматриваемом случае Um = Im·r, то выражение для средней мощности можно еще записать в виде

(2-23)

При данных амплитудах тока и напряжения выделяемая мощность будет тем меньше, чем больше угол сдвига фаз между ними. При сдвиге фаз 90° (рис. 2-14, б), что соответствует цепям с реактивными элементами - идеальными конденсаторами и катушками индуктивности без потерь, средняя мощность за период равна нулю, так как они в течение четверти периода запасают энергию, а в следующую четверть периода отдают ее обратно. Однако условно говорят о реактивной мощности Pр, отдаваемой и получаемой источником переменной э.д.с. при обмене энергией с реактивной нагрузкой, подразумевая под этим половину произведения амплитуд тока и напряжения на нагрузке на синус угла   между ними:

Или, если учесть, что напряжение на идеальной реактивной нагрузке Um = Im·X, то

(2-24)

(2-25)

В радиотехнических цепях часто приходится встречаться со случаем, когда на некотором ее участке действует переменное напряжение  , в то время как через него протекает постоянный ток и токи различных частот, кратных  :

Возникает вопрос о том, какой энергетический эффект получится в результате взаимодействия этих токов с напряжением круговой частоты  . Очевидно, что средняя за период мощность взаимодействия постоянного тока с переменным напряжением будет равна нулю. Половину периода она будет положительна - источник будет затрачивать энергию, а половину периода отрицательна - источнику будет возвращаться такая же энергия. Несколько сложнее обстоит вопрос о взаимодействии напряжения круговой частоты   с токами кратных частот n· . Для того чтобы найти среднюю мощность за период действия напряжения T, нужно, как и раньше, разбить период на столь малые отрезки времени  , в течение которых можно было бы считать ток и напряжения неизменными. Мощность, развиваемая на этом интервале,

Чтобы подсчитать среднюю мощность за время T, нужно умножить все pi на интервалы времени  , просуммировать эти произведения и разделить на период T. В рассматриваемом случае это приведет к суммированию произведений вида

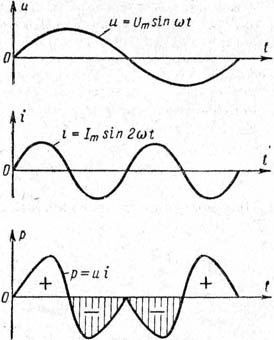
Нетрудно показать, что все суммы подобного вида равны нулю. На рис. 2-15 изображены напряжение и ток для случая, когда последний имеет вдвое большую частоту, чем напряжение (n = 2), а также график произведений их мгновенных значений. Из рассмотрения последнего видно, что мгновенная мощность также периодически изменяется во времени и дважды за время T переходит от положительных к таким же отрицательным значениям. Поэтому средняя мощность за время T будет равна нулю. Совершенно очевидно, что то же самое будет наблюдаться и при любом другом сочетании кратных частот.

Рис. 2-15. Мощность взаимодействия тока и напряжения кратных частот.

На основании рассмотрения, проведенного в настоящем параграфе, можно сформулировать весьма важный для дальнейшего вывод: если в цепи источника переменного напряжения протекают постоянный ток и переменные токи кратных частот, то энергетическое взаимодействие имеет место только с током, частота которого равна частоте источника напряжения; источник постоянного напряжения дает эффект энергетического взаимодействия только с постоянной составляющей проходящего через него тока.