1. Сопротивление Индуктивность, Емкость, Закон Максвела

2. Мощность

3. Работа

4. Источники ЭДС и тока. Условие эквивалентности (5 источников)

5. Законы Кирхгофа

6. Расчет цепей постоянного тока

7. Потенциальная диаграмма

8. Баланс мощности электрической цепи

9. Метод контурных токов

10. Метод узловых потенциалов

11. Методы преобразования цепей. (звезда - треугольник)

12. Принцип суперпозиции (наложение) только в магнитных цепях!

13. Метод эквивалентности генератора

14. Передача энергии от активного 2-х полюсника на нагрузку

15. Переменный ток (среднее значение переменного тока, действующее значение)

16. Активное сопротивление в цепях переменного тока

17. Индуктивность в цепях переменного тока

18. Емкость цепи переменного тока

19. Векторное значение Законов Кирхгофа

20. Мощности при переменном токе

21. Активная мощность емкость активное сопротивление индуктивность

22. Последовательное соединение RLC

23. Символический метод расчета , Формулы Элера

24. Цепь с последовательным соединением RLC комплексная проводимость

25. Вычисление мощностей в символической форме

26. Расчет индукции со взаимной индукции

1) Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему^[1]. Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как

где

R — сопротивление, Ом;

U — разность электрических потенциалов (напряжение) на концах проводника, В;

I — сила тока, протекающего между концами проводника под действием разности потенциалов, А.

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность^[1], краем которой является этот контур^[2][3][4].

В формуле

 — магнитный поток,   — ток в контуре,   — индуктивность.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока^[4]:

.

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током^[4]:

.

Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности^[4]. Элементами малой индуктивности (применяемыми для больших рабочих частот) могут быть одиночные (в том числе и неполные) витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников^[5].

Электри́ческая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками^[1].

В Международной системе единиц (СИ) ёмкость измеряется в фарадах.

Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид

где   — заряд,   — потенциал проводника.

Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ):

где ε₀ — электрическая постоянная, равная 8,854·10⁻¹² Ф/м, ε_r — относительная диэлектрическая проницаемость.

Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектрикомили вакуумом, — к конденсатору. В этом случае ёмкость (взаимная ёмкость) этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:

где S — площадь одной обкладки (подразумевается, что обкладки одинаковы), d — расстояние между обкладками, ε_r — относительная диэлектрическая проницаемость среды между обкладками.

Закон Максвелла (Электормагнитная индукция) При всяком изменении магнитного тока пронизывающего контур , в контуре наводится ЭДС прямопропорциональная скорости изменения потокосцепления контура во времени

2) Мо́щность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребленияэнергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени^[1].

Различают среднюю мощность за промежуток времени 

и мгновенную мощность в данный момент времени:

Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:

3) работаПри движении зарядов в электрической цепи выполняется работа. Численно работа, совершаемая при перенесении электрического заряда q между двумя точками, разность потенциалов между которыми равна U, может быть определена по формуле

  В свою очередь электрический заряд q может быть выражен как произведение величины тока на время:

  Подставляя значение заряда, получим

Итак, работа, совершаемая током на каком-либо участке цепи, прямо пропорциональна напряжению на этом участке, величине тока и времени, в течение которого протекает ток.

 Если принять U=1 в, I=1 a, t=1 сек, то А=1 в a сек

Эта единица работы называется джоулем.

Следовательно, 1 джоуль (дж), или ватт-секунда,-есть работа, выполняемая на участке цепи при напряжении 1 вольт, величине тока 1 ампер за 1 секунду.

Если в основной формуле выразить ток (или напряжение) по закону Ома то получим соответственно:

   В зависимости от типа потребителя процесс совершения работы электрическим током сопровождается превращением электрической энергии в другие виды энергии: тепловую (лампа накаливания, электронагревательные приборы), механическую (электрические двигатели), химическую ( электролиз, зарядка аккумуляторов), световую (газосветные лампы).

4) Источник ЭДС (идеальный источник напряжения) - двухполюсник, напряжение на зажимах которого постоянно (не зависит от тока в цепи). Напряжение может быть задано как константа, как функция времени, либо как внешнее управляющее воздействие.  В простейшем случае напряжение определено как константа, то есть напряжение источника ЭДС постоянно.  Реальные источники напряжения рузочная ХАРАКТЕРИСТИКА Идеальный источник напряжения (источник ЭДС) является физической абстракцией, то есть подобное устройство не может существовать. Если допустить существование такого устройства, то электрический ток I, протекающий через него, стремился бы к бесконечности при подключении нагрузки, сопротивление RH которой стремится к нулю. Но при этом получается, что мощность источника ЭДС также стремится к бесконечности, так как Р = EI. Но это невозможно, по той причине, что мощность любого источника энергии конечна. В реальности, любой источник напряжения обладает внутренним сопротивлением г, которое имеет обратную зависимость от мощности источника. То есть, чем больше мощность, тем меньше сопротивление (при заданном неизменном напряжении источника) и наоборот. Наличие внутреннего сопротивления отличает реальный источник напряжения от идеального. Следует отметить, что внутреннее сопротивление - это исключительно конструктивное свойство источника энергии. Эквивалентная схема реального источника напряжения представляет собой последовательное включение источника ЭДС - Е (идеального источника напряжения) и внутреннего сопротивления

5) Законы Кирхгофа Немецкий физик Г.Р. Кирхгоф в 1845 году установил законы равновесия в электрических цепях. Уравнения, составленные согласно этим законам, называются уравнениями Кирхгофа.

Первый закон Кирхгофа формулируется двояко:

1) алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю;

2) сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов

Согласно первой формулировки

При записи уравнений по этому закону токи, направленные к узлу и от узла, берутся с разными знаками. Например, для узла «d» электрической схемы, представленной на рисунке 1.9, уравнение имеет вид:

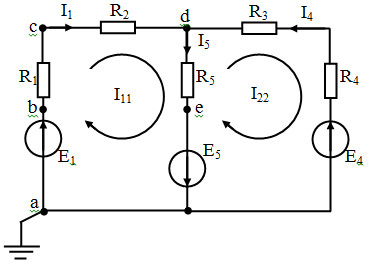
Рисунок 1.9 – Схема электрической цепи

Физический смысл первого закона Кирхгофа заключается в том, что в узлах электрической цепи не происходит накопления зарядов. Какое количество электричества в единицу времени подтекает к узлу, такое же и утекает от узла.

Второй закон Кирхгофа также можно сформулировать двояко:

1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура

При составлении уравнений по второму закону Кирхгофа произвольно выбирают направление обхода контура и все падения напряжений и ЭДС, направление которых совпадает с направлением обхода, берут со знаком «+», остальные со знаком «–». Например, для левого конура схемы, изображенной на рисунке 1.9, обходя его по часовой стрелке, можно записать

2) алгебраическая сумма напряжений (не падений напряжения) вдоль любого замкнутого контура равна нулю.

6) Расчет простых цепей постоянного тока

В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником.Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.  

Пример 1

  Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.

 

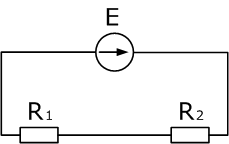
Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи. 

Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов. 

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем. 

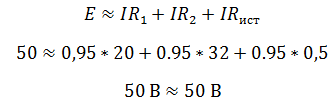
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.

В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками. 

Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.

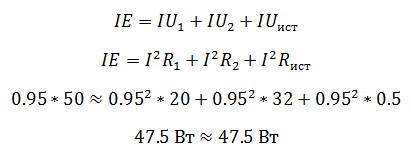
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.

7) 1.7 Потенциальная диаграмма

/

Потенциальной диаграммой называют график распределения потенциалов вдоль участка электрической цепи или замкнутого контура.

При расчете потенциалов одну (любую) точку можно заземлить, принимая ее потенциал равным нулю. На потенциальной диаграмме эту точку помещают в начало координат. По оси абсцисс откладывается в масштабе величина сопротивления участка, а по оси ординат – значение потенциала соответствующей точки.

Рисунок 1.9 – Схема электрической цепи

Рассмотрим пример построения потенциальной диаграммы. Пусть для схемы, изображенной на рисунке 1.9, известны токи: I1=2А; I5=3А; I4=1А, значения ЭДС: Е1=5В; Е5=8В; Е4=3В и значения сопротивлений: R1=2Ом; R2=3Ом; R5=1Ом; R3=5Ом; R4=3Ом. Требуется построить потенциальную диаграмму контура «abcdea».

Заземлим точку «а», приняв ее потенциал φа=0. Найдем потенциалы остальных точек контура:

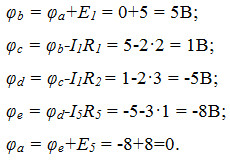
По полученным данным строим потенциальную диаграмму (рисунок 1.10).

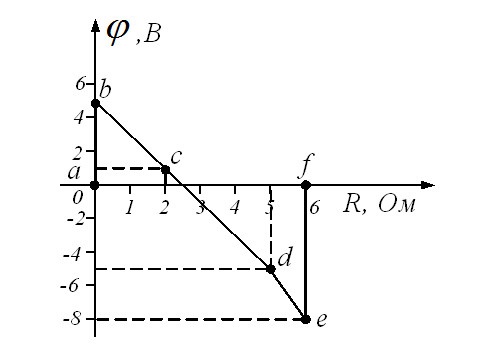
Рисунок 1.10 – Построение потенциальной диаграммы

8) Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками. То есть если источник ЭДС в цепи отдает 100 Вт, то приемники в этой цепи потребляют ровно такую же мощность. 

Или

9) Ме́тод ко́нтурных то́ков — метод сокращения размерности системы уравнений, описывающей электрическую цепь. Метод контурных токов — метод расчёта электрических цепей, при котором за неизвестные принимаются токи в контурах, образованных некоторым условным делением электрической цепи.

10) Метод узловы́х потенциалов — метод расчета электрических цепей путём записи системы линейных алгебраических уравнений, в которой неизвестными являются потенциалы в узлах цепи. В результате применения метода определяются потенциалы во всех узлах цепи, а также, при необходимости, токи во всех ветвях.

11) треугольник в звезду

Расчет и исследование сложных электрических цепей во многих случаях можно значительно облегчить и сделать более наглядным путем преобразования электрических схем одного вида в схемы другого вида. Одним из способов является эквивалентное преобразование треугольника в звезду. В этом методе выполняется преобразование пассивной части электрической цепи, т.е. приемников электрической энергии.

Определение соединения сопротивлений треугольником

Если три сопротивления соединены так, что образуют собою стороны треугольника, то такое соединение сопротивлений называют треугольником сопротивлений.

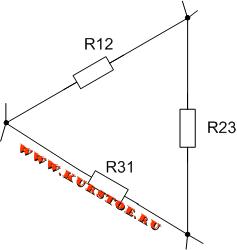
Обычно в курсе электротехники принято элементы рисовать только горизонтально и вертикально. На следующем рисунке так же представлено соединение треугольником.

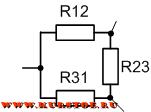
Определение соединения сопротивлений звездой

Если соединение трех сопротивлений имеет общий узел и имеет внешний вид трехлучевой звезды, то такое соединение сопротивлений называется звездой.

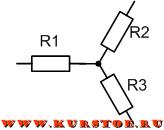
Причина преобразования треугольника в звезду

При расчете электрической цепи бывают случаи, когда нет ни последовательных, ни параллельных соединений сопротивлений. В этом случае можно попробовать отыскать соединение сопротивлений треугольником и выполнить экивалентное преобразование треугольника в звезду.

Если в электрической цепи нашли соединение сопротивлений треугольником, то в узлы соединения сопротивлений подставляем концы лучей соединения сопротивлений в виде звезды.

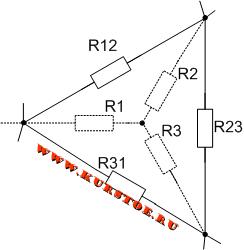
 Далее убираем (удаляем первоначальное) соединение треугольником. В результате получается эквивалентное соединение звездой.