Тригонометрія
ЗНАКИ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ
|
Чверть |
|
|
tg |
ctg |
0 < < |
I |
+ |
+ |
+ |
+ |
< < |
II |
+ |
- |
- |
- |
< < |
III |
- |
- |
+ |
+ |
<
<
|
IV |
- |
+ |
- |
- |
ТАБЛИЦЯ ЗНАЧЕНЬ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ КУТІВ
|
0° |
30° |
45° |
60° |
90° |
120° |
135° |
150° |
180° |
270° |
f( ) |
0 |
|
|
|
|
|
|
|
|
|
sin
|
0 |
|
|
|
1 |
|
|
|
0 |
-1 |
cos |
1 |
|
|
|
0 |
|
|
|
-1 |
0 |
tg |
0 |
|
1 |
|
- |
|
-1 |
|
0 |
- |
ctg |
- |
|
1 |
|
0 |
|
-1 |
|
- |
0 |
СПІВВІДНОШЕННЯ МІЖ ТРИГОНОМЕТРИЧНИМИ ФУНКЦІЯМИ ОДНОГО І ТОГО Ж АРГУМЕНТУ
1
+ tg2
=
,
= 1,
1
+ ctg²
=
,
tg
· ctg
= 1.
ФОРМУЛИ ДОДАВАННЯ
=
+
,
=
-
,
=
+
,
=
+
,
=
=
.
ФОРМУЛИ ПОДВІЙНОГО АРГУМЕНТУ
=
,
=
-
= 2
- 1 = 1 - 2
,
=
.
ФОРМУЛИ ПОЛОВИННОГО АРГУМЕНТУ
=
,
=
,
=
=
=
.
ФОРМУЛИ ПОНИЖЕННЯ СТЕПЕНЯ
cos²
=
,
sin²
=
.
ФОРМУЛИ ПЕРЕТВОРЕННЯ СУМИ В ДОБУТОК
НАЙПРОСТІШІ ТРИГОНОМЕТРИЧНІ РІВНЯННЯ
Рівняння вигляду sin х=а.
При | а | > 1 розв'язків немає.
При
<
1
х
= (-1)n
аrcsіn
+
n,
n
.
Окремі випадки.
а
= 0,
sin
х =
0,
=
n,
n
;
а = 1, sin х = 1, х = +2 n, n ;
а
= -1, sin
х
= -1, х =
+2
n,
n
.
Рівняння вигляду соs х = а.
При | а | > 1 розв'язків немає.
При
1
х
=
аrccos
+
2
n
, n
.
Окремі випадки.
а = 0, cos a = 0, х = + n, n ;
а = 1, cos a = 1, = 2 n, n ;
а = -1, cos х = -1, х = + 2 n, n .
Рівняння вигляду tg х = а, х = аrctg + n, n .
Рівняння
вигляду ctg
х = а,
х
= аrcctg
+
.
ПОХІДНА
Похідною функції у = f(х) у точці х0 називається границя
=
y' (x0),
де
х
— приріст аргументу в точці х0.
ПРАВИЛА ДИФЕРЕНЦІЮВАННЯ
Якщо с - стала, функції u(х), u1(х) і v(х),— диференційовані у точці х0, то в цій точці справедливі формули:
1. с'= 0,
2. (с u)' = cu'
3. (u1 + u 2 + ... + u п)' = u 1' + u 2' + ... + u n',
4. (uv)' = u'v + uv',
5.
=
,
v≠0.
ПОХІДНА СКЛАДЕНОЇ ФУНКЦІЇ
Нехай у = F(u), u = u (х), і у(х) = F(u (х)) — складена функція. Якщо функція u(х) диференційована в точці х0 і функція F(u) диференційована в точці u 0 = u(х0), то функція у(х) = F(u (х) ) диференційована в точці х0 і її похідна дорівнює :
y'(x0) = F'(u0) · u'(x0).
ТАБЛИЦЯ ПОХІДНИХ
1. (ха)'= axa-1, а - дійсне число,
a)
=
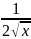, б)
=
.
2. (sin x)' = cos x.
3. (cos x)' = - sin x.
4.
(ctg x)'
=
-
.
5.
(tg x)'
=
.
6.
(loga
x)'
=
,
(ln x)'
=
.
7. (ax)' = ax ln a , (ex)' = ex.
8. (xx)' = xx (ln x + 1).
9.
(arcsin x)'
=
.
10.
(arccos x)'
=
.
11.
(arcctg x)'
=
.
12.
(arcctg x)'
=
.
НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
Функція F(х) — первісна функції f(х) на проміжку X (скінченному або нескінченному), якщо для всіх х з цього проміжку
F'(х) = f(x).
Невизначений інтеграл від функції f(х) на проміжку X — множина всіх її первісних:
ОСНОВНІ ФОРМУЛИ ІНТЕГРУВАННЯ
(ТАБЛИЧНІ ІНТЕГРАЛИ)
1.
=
+
C (a ≠ -1).
2.
= ln
+ C.
3.
= -cos x + C.
4.
= sin x + C.
5.
= -ln
+ C.
6.
= -ln
+ C.
7.
= - ctg x + C.
8.
= tg x + C.
9.
=
+ C.
10.
=
ex
+ C.
ТАБЛИЦЯ КВАДРАТІВ ДВОЗНАЧНИХ ЧИСЕЛ
Десятки |
Одиниці |
||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 2 3 4 5 6 7 8 9 |
121 441 961 1681 2601 3721 5041 6561 8281 |
144 484 1024 1764 2704 3844 5184 6724 8424 |
169 529 1089 1849 2809 3969 5329 6889 8649 |
196 576 1156 1936 2916 4096 5476 7056 8836 |
225 625 1225 2025 3025 4225 5625 7225 9025 |
256 676 1296 2116 3136 4356 5776 7396 9216 |
289 729 1369 2209 3249 4489 5819 7569 9409 |
324 784 1444 2304 3364 4624 6084 7744 9604
|
361 841 1521 2401 3481 4761 6241 7921 9801 |