2. Розв’язування нерівностей

23. < 0.

Розв'язання:

Оскільки знак дробу збігається із знаком добутку, то дана нерів­ність рівносильна нерівності (7 - х)(х + 2) < 0.

Маємо (7 - х)(х + 2) = 0, х₁ = 7, х₂ = -2.

Отже, розв'язком даної нерівності є проміжки: ( ; -2) і (7; + ).

Відповідь. ( ; -2) і (7; + ).

2 4. < 0,

х² + 3х – 4 0.

Розв'язання:

Розв'яжемо окремо кожну з нерівностей:

а) < 0. Оскільки х² + 3 > 0 для будь-якого х, отже, 2х - 7 < 0,

звідки х < 3,5. Отже, х ( ; 3,5).

б) х² + 3х – 4 0. х² + 3х – 4 = 0, х₁ = -4, х₂ = 1. Отримаємо нерівність (х + 4)(х-1) 0. Отже, х ( ; -4] [1; + ).

Відповідь. х ( ; -4] [1; 3,5).

25. Розв'язати нерівність .

Розв'язання:

Врахувавши, що 0 < і = маємо:

х - 2; 0.

Остання нерівність рівносильна системі (х – 3)(х+ 1)х 0,

х ≠ 0.

Ліва частина нерівності (х - 3)(х + 1)х 0 дорівнює нулю в точках х = 3, х = -1, х = 0. Відкладемо ці точки на числовій прямій і вста­новимо знаки виразу (х - 3)(х + 1)х на утворених проміжках.

Врахувавши, що х ≠ 0, розв'язками даної нерівності є проміжки:

-1 х < 0; х 3.

Відповідь. х [-1; 0) [3; + ).

26. Розв'язати нерівність log_cos1 (х² - х) log_cos1 (х + 3).

Розв'язання:

х(х – 1) > 0,

х² - 2х – 3 0,

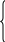
х > 1,

х < 0,

-1 х 3,

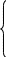х² - х > 0,

х + 3 > 0,

х² - х х + 3,

х > 1,

-1 х 3,

х < 0,

-1 х 3.

Отже, х [-1; 0)𝚄(1; 3].

Відповідь. [-1; 0)𝚄(1; 3].

4. Функція

27. Знайти область визначення функції у =

Розв'язання:

Областю визначення даної функції є множина розв'язків системи:

отже, х [-1; 0] [1; 3) (3; + ).

х [-1; 0] [1; + ),

х ≠ 3,

х³ - х 0,

х – 3 ≠ 0;

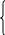
Відповідь. D(у) = [-1; 0] [1; 3) (3;+ ).

28. Знайти область визначення функції у =

Розв'язання:

Областю визначення даної функції є множина тих значень змінної х, які задовольняють умову 0. Оскільки, х² 0 і 0 для будь-яких х, то вказана нерівність справджується для будь-яких х. Отже, областю визначення даної функції є множина дійсних чисел.

Відповідь. D(у) = (- ;+ ).

29. Вказати проміжки зростання функції у = .

Розв 'язання:

Оскільки х² - х ≠ 0, тому D(у) = (- ;0) (0; 1) (1; + ).

У результаті перетворень отримаємо:

у = .

Отже, дану функцію можна записати так: у = -

Графіком цієї функції є гіпербола з виколотою точкою А(1; -5).

Функція зростає на проміжку (- ;0); (0; 1) та (1; + ).

Відповідь. (- ;0); (0; 1) та (1; + ).

30. Вказати множину значень функції у = |х + 2| - | х | .

Розв'язання:

Областю визначення функції є множина R. Розіб'ємо її на проміж­ки числами, при яких вирази під знаком модуля перетворюються в нуль. Отримаємо проміжки (- ;-2); [-2; 0);[0;+ ;). Знайдемо фор­мулу, якою задається функція на кожному з них:

х (- ; -2); у = -х-2 + х = -2; у = -2;

х [-2;0); у = х + 2 +х = 2х + 2; у = 2х + 2;

х [0; + ); у = х + 2-х = 2; у = 2.

Множиною значень функції у =| х + 2| -|х| є проміжок [-2; 2].

Відповідь. [-2; 2].

31. Не будуючи графіка функції, знайти точки перетину його з ося­ми координат: у = 3х² - 4х - 7.

Розв'язання:

Графік функції перетинає вісь Ох у точках, в яких у = 0.

3х² - 4х - 7 = 0;

х₁ = 2 ; х₂ = -1.

Отже, графік функції перетинає вісь Ох в точках (- 1; 0), (2 ; 0).

Точкою перетину графіка з віссю Оу буде точка, абсциса якої дорівнює нулю: х = 0; у = -7.

Отже, графік функції перетинає вісь Оу в точці (0; -7).

Відповідь. (-1; 0), (2 ; 0) - точки перетину графіка з віссю Ох; (0; -7) - з віссю Оу.