Понятия о структурной и функциональной схеме, элементарные динамические звенья (эдз).

В автоматике существует понятие структурной и функциональной схемы устройства. Всякая техническая система (самолет, станок) при создании сначала рассчитывается математически. Одним из важнейших параметров системы, который рассчитывается до фактического создания этой системы, является устойчивость. Система называется устойчивой, если будучи выведенной из состояния равновесия, она возвращается в установленное состояние после снятия возмущающего воздействия.

После создания структурной схемы устройства система описывается математически. Получается сложная система дифференциальных уравнений выше второго порядка. Решение их затруднительно, поэтому вводится понятие элементарных динамических звеньев. Под элементарным динамическим звеном понимают устройство или часть его, которая описывается дифференциальным уравнением не выше второго порядка. Физического смысла ЭДЗ не имеет, это понятие введено только для облегчения расчетов. Структурная схема системы состоит из элементарных динамических звеньев, а функциональная - из функциональных узлов (двигатель, усилитель и т.д.) Один функциональный узел может быть представлен несколькими элементарными динамическими звеньями.

В ТАР обычно рассматриваются следующие звенья: безинерционное, апериодическое I порядка, апериодическое II порядка (колебательное), дифференцирующее, и интегрирующее.

В САР различные элементы систем могут иметь разную конфигурацию, в них могут использоваться разные физические явления, но для анализа работы системы важны только статические и динамические характеристики связывающие входные и выходные сигналы действующие на входе и выходе отдельного звена или всей системы. Статические характеристики характеризуют свойства звена в установившемся режиме, т.е. при неизменном входном сигнале.

Динамические характеристики выявляются при переходном процессе, т.е. при переходе звена или системы из одного устойчивого состояния в другое при подаче внешнего возмущающего воздействия. Характеристики звеньев полностью определяются с помощью дифференциальных уравнений которые отражают характер изменения выходных сигналов при заданном входном сигнале.

В реальных условиях САУ не может находится все время в установленном режиме, т.к. на нее воздействует внешнее возмущающее воздействие, стремящееся хотя бы кратковременно изменить значение регулируемой величины. К числу внешних возмущений можно отнести любое изменение установившегося значения управляемой величины и внешнего воздействия , изменения параметров самой системы или изменение окружающих условий, например влажности. Исследование установившегося режима позволяет определить погрешность, т.е. решить вопрос о пригодности САУ (САР).

САУ (САР) должна быть устойчивой по отношению к внешним возмущениям. Для решения вопроса об устойчивости необходимо исследовать переходный процесс. Внешнее возмущение может быть случайным, кратковременным, в таком случае после окончания переходного процесса регулируемая величина должна вернуться к прежнему значению. Внешнее возмущение может носить стационарный характер. При этом регулируемая величина в устойчивой системе стремится к новому установленному значению. Под внешним возмущением понимают изменение внешнего воздействия или управляющей величины.

В автоматике рассматривают след виды возмущений.

1) 2) 3)

х х х

1

t

t t

1. Сигнал возрастает с пост скоростью;

2. Единичный скачек;

3. Гармонический сигнал единичной амплитуды.

Дифференциальные уравнения ЭДЗ, методы их решения,

передаточная функция.

1. Б езинерционное звено. y y

y = k * x x

t

Например усилитель постоянного тока передает вх. сигнал на выход без задержки. Примером безинерционных звеньев является потенциометрический датчик, сельсин…

2. Апериодическое звено I порядка.

T=R*C

Выходная величина достигает установившегося значения с запаздыванием, которое определяется постоянной времени звена (фильтр низких частот или интегрирующее звено)

у T x

y

x

3. Дифференцирующее звено

T=R*C

Выходная величина пропорциональна производной от входной.

y

y x

y t

4. Интегрирующее звено

Выходная величина пропорциональна интегралу от вх. величины.

Т.к. при исследовании систем автоматического регулирования приходится исследовать несколько дифференциальных уравнений, то общее уравнение системы оказывается системой дифференциальных уравнений или описывается дифференциальным уравнением выше второго порядка.

Чтобы облегчить решение дифференциальных уравнений применяется прямое и обратное преобразование Лапласа. С помощью прямого преобразования Лапласа по заданному значению функции f(t) которое называется оригиналом находится изображение f(p).

Находится с помощью прямого преобразования Лапласа

p – называют оператором Лапласа

С помощью преобразований Лапласа дифференциальные уравнения решаются следующим образом:

• оригиналы заменяются их изображениями по Лапласу

• дифференциальное уравнение превращается в алгебраическое уравнение, из которого находится изображение выходной величины.

• с помощью обратного преобразования Лапласа находится оригинал y(p)=y(t)

Существуют таблицы прямого и обратного преобразования Лапласа для наиболее распространенных функций. Из уравнения звена в операторной форме можно найти передаточную функцию звена.

Передаточной функцией звена называют: Отношение изображения выходной величины к изображению входной величины при нулевых условиях.

Например для апериодического звена II порядка:

;

;

Характеристики звеньев.

Переходная функция h(t) является динамической характеристикой. h(t)- это закон изменения выходной величины, при изменении входной величины по закону единичного скачка.

h(t)- является оригиналом функции Y(p) при подаче на вход единичного скачка. Оригинал входной функции X(t)=1, изображение X(p)=1/p.

Пример: для интегрирующего звена. ;

С помощью обратного преобразования Лапласа находим h(t):

Переходной характеристикой ЭДЗ называют график изменения во времени выходной величины при изменении входной величины по закону единичной ступенчатой функции.

Переходные характеристики и переходные функции ЭДЗ.

Переходные процессы в ЭДЗ исследуются при подаче на вход звена единичного скачка, они характеризуют переход ЭДЗ из одного устойчивого состояния в другое. Переходный процесс является динамическим состоянием системы. Формула переходной характеристики называется переходной функцией h(t) и находится решением дифференциального уравнения звена, при подаче на его вход единичного скачка.

Например: , переходная функция

апериодического звена I порядка.

где: Т – постоянная времени звена;

k – коэффициент передачи.

Проще записать дифференциальное уравнение в апператорной форме, заменив входную функцию ее изображением. Если на входе 1, то ее изображение 1/р

- заменим оператором Лапласа, решив уравнение в операторной форме, получим изображение выходной величины. С помощью обратного преобразования Лапласа получим Y(t) который и будет являться переходным процессом.

Графики переходного процесса представляют собой переходную характеристику. Качество переходного процесса определяется его длительностью, величиной выброса и периодом колебаний. Качество переходного процесса определяет работоспособность системы автоматического регулирования и в первую очередь устойчивость.

Частотные характеристики звеньев.

Частотными характеристиками звеньев называются зависимости амплитуды и фазы синусоидальных колебаний от частоты при прохождении этих колебаний через ЭДЗ. На входе ЭДЗ действует сигнал гармонический единичной амплитуды.

Под длительным влиянием входного гармонического воздействия выходная величина также изменяется гармонически с той же частотой, но амплитуда и фаза изменяются. При неизменной амплитуде входного сигнала амплитуда и фаза выходного сигнала зависит от параметров звена и от частоты входного гармонического воздействия. Если изображение входного сигнала:

, то выходного

Комплексный коэффициент W(jw) определяется как изображение выходной величины ко входной, и называется годограф.

W(jw) называется также амплитуднофозочастотной характеристикой,

он показывает, как изменяется W(jw)= A_ye^jφ, амплитуда и фаза выходного сигнала при нулевой фазе и единичной амплитуде входного сигнала.

Комплексный коэффициент передачи может быть получен из коэффициента передачи звена подстановкой вместо р – jw. W(jw) как всякое комплексное число имеют действительную и мнимую части и изображаются н а комплексной плоскости вектором:

Для апериодического звена I порядка:

Вектор характеризуется модулем и фазой:

Q(w) A(w)

φ 1

P(w) Q(w)

w	A(w)	φ(w)
0	k	0
		-450
	0	-900

Из рассмотрения АЧХ и ФЧХ характеристик звеньев можно установить , что разные звенья по разному воспроизводят входной гармонический сигнал. Диапазон частот в пределах которого амплитудные и фазовые искажения не превышают допустимого значения Называется полосой пропускания звена.

Полоса пропускания безинерционного звена равна бесконечности. Апериодическое звено I порядка пропускает нижние частоты и ослабляет верхние. Дифференцирующее звено пропускает верхние и ослабляет нижние частоты. Апериодическое звено II порядка ослабляет верхние и нижние частоты и усиливает средние. Полоса пропускания звена зависит от его постоянной времени. Чем меньше Т, тем больше полоса пропускания. По ширине полосы пропускания судят о длительности переходного процесса.

Логарифмические частотные характеристики

Построение АЧХ и ФЧХ является трудоемким процессом, т.к. нужно находить значение A(w) и Q(w) для каждого значения (w).

Проще исследовать устойчивость САР состоящей из нескольких звеньев с помощью логарифмических характеристик. Строится ЛАЧХ и ЛФЧХ в логарифмическом масштабе, по оси абсцисс откладываются значение частоты в логарифмическом масштабе. Если частота изменяется в 10 раз, то такое возрастание называют декадой, если в 2 раза, то октавой.

по оси ординат откладывают L(w) в децибелах.

L(w)=20 lg A(w)

6 0 k=100

4 0

2 0 20 lg k

10 100 1000

Белл является логарифмической единицей соответствующей

10-кратному увеличению мощности.

Т.к. L(w) в децибелах, то умножаем логарифм на 10. Т.к. A(w) является не отношением мощностей, а отношением напряжений, то умножаем логарифм на 2. При построение логарифмических характеристик в начале координат по оси абсцисс ноль не ставят, а обязательно конечное значение. Т.к.

дБ

дБ

дБ

Пример: Апериодическое звено I порядка.

20 lg k

w_c

10 100

-20 дБ/дек.

-20

Первое слагаемое не зависит от частоты и направления оси абсцисс. Второе зависит и для его построения можно воспользоваться асимптотической логарифмической характеристикой.

Разбиваем весь диапазон частот на 2 интервала:

1. От

0

На этом интервале второе слагаемое изображается прямой совпадающей с осью абсцисс.

2. От

0

На этом интервале второе слагаемое изображается прямой пропорциональной изменению частоты. Определим наклон этой прямой:

20 дБ

С увеличением частоты в 10 раз второе слагаемое изменяется на -20 дБ. Принято говорить, что прямая имеет наклон –20 децибел на декаду.

При построении асимптотической логарифмической характеристики наибольшая ошибка получается в точке w_сопр, эта ошибка = 3 дБ.

дБ

Правила построения ЛАЧХ апериодического звена I порядка.

1. Находим на плоскости точку с координатами ( ).

2. Влево от этой точки проводим прямую параллельную оси абсцисс.

3. Вправо проводим прямую с наклоном –20 дБ на декоду.

Для перехода от асимптотической характеристики к реальной нужно в точке ( ) уменьшить значение ординаты на 3 дБ.

Выражение фазочастотной характеристики:

По оси абсцисс откладывается частота в логарифмическом масштабе, а по оси ординат откладывается частота, в радианах или градусах.

ЛФЧХ для апериодического звена I порядка начинается в нуле, на частоте проходит через –45⁰ и стремится к –90⁰.

φ

w

-45⁰

-90⁰

Виды соединений звеньев

Существует 3 вида соединения:

• последовательное;

• параллельное;

• встречно-параллельное.

x (p) У₁(p) У₂(p)

W₁(p) W₂(p)

x(p) У(p)

W₁(p) W₁(p)

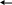W₂(p) W₂(p)

Последовательным называется такое соединение звеньев, при котором выходная величина предыдущего звена является входной величиной для последующего звена.

Передаточная функция последовательного соединения звеньев равна произведению передаточной функции последовательно соединенных звеньев. Логарифмическая АЧХ последовательно соединенных звеньев равна сумме ЛАЧХ отдельных звеньев. ФЧХ последовательно соединенных звеньев представляет собой сумму ФЧХ

Встречно-параллельное соединение звеньев

В стречно-параллельным соединением звеньев называют охват одного звена или нескольких звеньев соединенных последовательной обратной связью. Связь бывает положительная и отрицательная

x(p) У₁(p) У(p)

W₁(p) W₁(p) – передаточная характеристика

звена

W₂(p) У₁(p) – выходная характеристика

звена

Передаточная функция встречно-параллельного соединения звеньев равна передаточной функции звена охваченного обратной связью, деленной на сумму 1+ произведение функций (если связь отрицательная) и 1- произведение функций (если связь положительная). В системе автоматического регулирования чаще всего применяется отрицательная обратная связь. Если в качестве звена обратной связи используют безинерционное звено, например усилитель, связь называется жесткой. Гибкая обратная связь может быть скоростной и изодромной. При скоростной ОС второе звено является идеальным дифференцирующим. При изодромной ОС второе звено является реальным дифференцирующим.

Устойчивость линейных систем автоматического регулирования

САР называется устойчивой, если будучи выведенной, из состояния равновесия, она возвращается в устойчивое состояние после снятия возмущающего воздействия.

Выходной сигнал состоит из свободных колебаний и вынужденных.

y(t) = y_св(t) + y_вын(t)

Свободные колебания определяются свойствами системы и начальными условиями. Они характеризуют переходный процесс. Вынужденные колебания определяются возмущающим воздействием и свойствами системы.

Если система устойчивая, то y_своб стремится к 0, при Т стремящемся к бесконечности. y_вын характеризует изменение выходной величины установленной под воздействием управляющего сигнала. Так как система должна воспроизводить входной сигнал с малой ошибкой, то y_вын(t) должна быть близка к x(t).

Переходный процесс устойчивой системы имеет такой вид, если система находится на границе устойчивости, то в ней возникают незатухающие колебания. Если система неустойчива, то колебания нарастают по экспоненте.

y(t) y(t)

t t

Создано несколько критериев для определения устойчивости. Критерии бывают математические, которые рассматривают характеристические уравнения системы.

Критерии Рауса-Гурвица – в этом критерии рассматриваются корни характеристического уравнения системы. Чтобы система была устойчивой действительные части всех корней характеристического уравнения должны быть отрицательными. Существуют частотные критерии устойчивости, такие как критерии Михайлова и Найквиста. Проще всего определять устойчивость системы с помощью логарифмических ЛАЧХ и ЛФЧХ.

L(w)

w_кр w

w_ср

φ(w)

w

-180⁰

Чтобы в системе существовали незатухающие колебания, должны выполняться баланс фаз и баланс амплитуд.

В точке w_ср выполняется условие баланса амплитуд A(w) = 1; k_y * k_ос = 1.

На частоте w_кр выполняется условие баланса фаз φ(w) = -180⁰. Цепи обратной связи поворачивают фазу еще на 180⁰ и колебания приходят на вход в фазе, в системе поддерживаются незатухающие колебания, если w_ср и w_кр совпадут.

Если в точке w_ср φ(w) отличается от -180⁰ на угол не меньше 45⁰ в положительную сторону, то такая система имеет запас устойчивости по фазе.

В точке w_кр L(w) должно быть меньше 0. С запасом устойчивости по амплитуде не меньше 10 дБ. Так как построение ЛАЧХ и ФЧХ производится всего по одной точке, то такой способ определения устойчивости является самым простым.

Критерии устойчивости.

Все критерии устойчивости основываются на том факте, что система устойчива, тогда, и только тогда, если все корни характеристического уравнения расположены в левой части комплексной плоскости, т.е. их действительные части отрицательны. Гурвиц не занимался ТАРом, но исследовал характеристические уравнения и вывел эту закономерность: что если определители характеристического уравнения положительны и а₀>0, то все корни имеют отрицательные действительные части.

j

р₃*

1

р₂*

р₁*

Если корень имеет отрицательную действительную часть или действительный корень отрицательный, то свободные колебания в системе являются затухающими, следовательно система является устойчивой.

- е^-рt

Характеристическим называют уравнение, которые представляют собой знаменатель передаточной функции.

Правила построения матрицы: в левом углу пишется а₁, по диагонали, пишутся коэффициенты с возрастающими номерами.

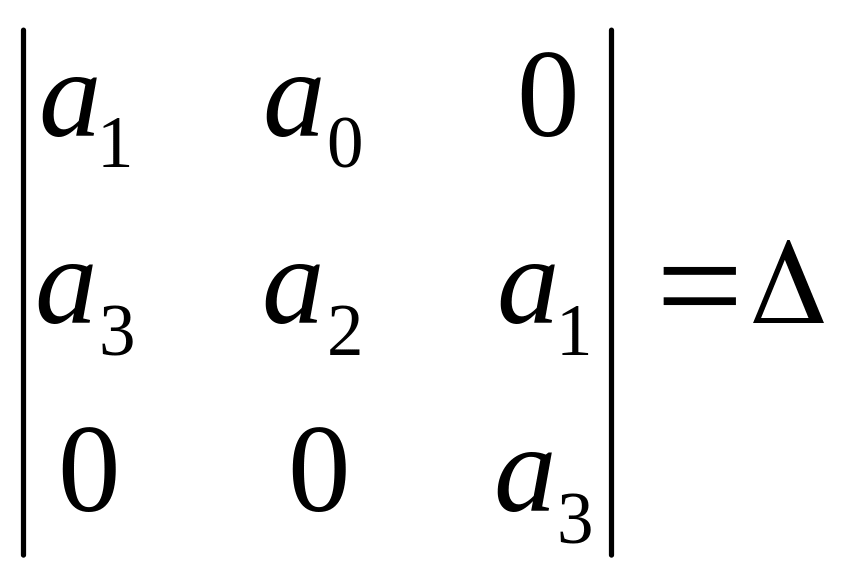
Возможен и второй способ построения матрицы. В левом от а₁ и дальше с убывающими номерами, следующий с а₃, то есть в первом столбце записаны коэффициенты с нечетными номерами. Гурвиц доказал, что действительные части комплексных корней и действительные корни будут отрицательны, если а₁>0 и все определители Гурвица будут больше 0.

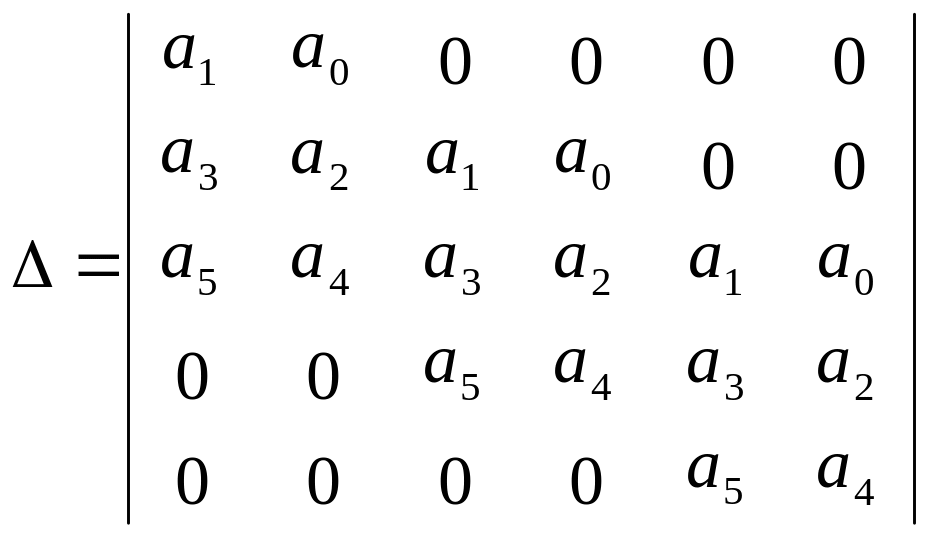
Если все корни характеристического уравнения отрицательны, то система устойчива. Проще исследовать систему с помощью частотного критерия Михайлова и Найквиста.

Критерий Михайлова рассматривает устойчивость замкнутой системы.

Ф(р) Это уравнение замкнутой системы.

В полиноме N(p) заменяют р на jw и строят на комплексной плоскости векторы N(jw) для разных значений w от 0 до . Концы этих векторов очерчивают кривую называемую годографом Михайлова. Годограф вращается против часовой стрелки.

Если годограф последовательно описывает n четвертей комплексной плоскости, где n – степень многочлена то система устойчива.

Например, для многочлена 3-ей степени (n=3), если система устойчива, годограф проходит последовательно три квадранта комплексной плоскости.

n =2

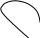
n=1

n=3

n=4

система устойчива система на границе система неустойчива

устойчивости

Если годограф проходит через начало координат, то система находится на границе устойчивости.

Если годограф пропускает какой-либо квадрант, то система неустойчива.

Критерий Найквиста - Этот критерий позволяет судить об устойчивости замкнутой системы по амплитуднофазочастотной характеристике разомкнутой системы.

Критерии Михайлова применяются для анализа замкнутых систем автоматического регулирования. В основе всех критериев лежит тот факт , что система является устойчивой , если все действительные части и действительные корни отрицательны.

В первоначальном виде критерий Михайлова формируется так: система устойчива, если при изменении частоты w от 0 до , изменение N(jw) будет nπ, где n – порядок характеристического уравнения.

Характеристическое уравнение может быть записано так:

где, p₁, p₂…p_n – корни уравнения.

получено заменой р на jw.

Каждое выражение в скобках представляет собой разность векторов jw и р_i , т.е. элементарный вектор на комплексной плоскости, начинающийся в точке р_i и заканчивающийся в точке jw. Произведение векторов (jw - р_i) есть вектор N(jw) , модуль которого равен произведению модулей элементарных векторов, а arg равен сумме:

Если все корни характеристического уравнения лежат в левой полуплоскости комплексной плоскости, то т.к. при изменении частоты от до arg каждого элементарного вектора изменится на (против часовой стрелки), суммарное изменение arg N(jw), будет для устойчивой системы (все корни имеют отрицательную действительную часть).

jw

jw-p₁ jw-p₂

p₁ p₂

Если один из корней характеристического уравнения имеет положительную действительную часть, то его arg при изменении частоты от до arg изменится на (по часовой стрелке), то система неустойчива.