Колебания в реальном колебательном контуре.
Реальный колебательный контур характеризуется наличием активных потерь. На этом активном сопротивлении происходит энергии, поэтому колебания затухают. Они затухают по экспоненте.
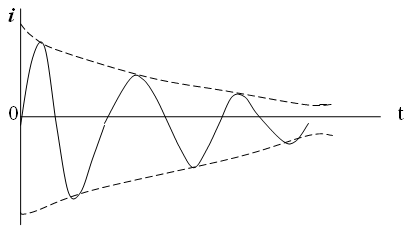
δ=Rп/Zв – коэффициент затухания. Он тем больше, чем больше активные потери.
Добротность контура:
Q=1/δ= Zв/Rп - величина обратная затуханию и чем меньше активные потери, тем больше её величина.
Свободные колебания в реальном контуре происходят на частоте собственных колебаний контура и являются затухающими.
Последовательный колебательный контур.
Ц
епь
состоящая из источника гармонических
колебаний, катушки индуктивности и
емкости соединенных последовательно.
Все активные потери в контуре собраны
в сопротивление R.
Эти потери в соединительных проводах,
в проводе обмотки катушки и в диэлектрике
конденсатора. В контуре наблюдаются
вынужденные колебания на частоте
генератора. Эти колебания не нарастают
и не опадают скачком, т.к. при включении
и выключении в контуре возникают
собственные колебания на частоте
вынужденных.
По закону Кирхгофа:
E=ImRп+ImX
X=XL-XC
Построим векторные диаграммы для трех случаев:
1. ωr>ω0, XL>XC
E опережает ток на угол π/2, т.е. контур представляет собой индукивно – резистивное сопротивление.
2.ωг=ω0, XL=XC X=XL-XC
Резонансом называется явление при котором X=0 (XL-XC=0), т.е. XL=XC. Контур представляет собой чисто активное сопротивление, равное сопротивлению потерь в контуре. Е совпадает по фазе с током и равна падению напряжения на активном сопротивлении контура.
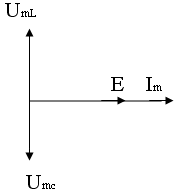
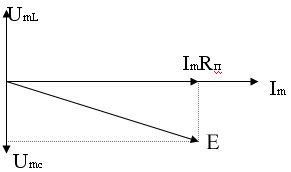
3. ωг<ω0, XL<<XC
E отстает от тока на угол меньше 90˚, т.е. контур представляет собой емкостно-резистивное сопротивление.
Входное сопротивление последовательного колебательного контура.
ZВХ=Rп+jX
X=XL-XC=ωL-1/ωC= ωLω0/ω0- ω0/ω0 ωC= ω0L(ω/ω0-ω0/ω)= ZВ(ω/ω0-ω0/ω)= ZВ((ω²-ω0²)/ω0ω)= ZВ((ω-ω0)(ω+ω0)/ω0ω)≈ ZВ(2∆ω/ωω0)= ZВ-2∆ω/ω0
Предполагаем, что расстройка контура относительно частоты ω0 невелика(ω≈ω0) ω-ω0=∆ω
∆ω- абсолютная расстройка контура относительно ω0
∆ω/ω0 – относительная расстройка контура
│ZВx│=√(Rп²+X²)=√(Rп²+ZВ²4(∆ω/ω0)²) – модуль входного сопротивления. Изменение ZВx от частоты называется частотной характеристикой сопротивления.
│ZВx│/ ZВxRп=√(1+Q²4(∆ω/ω0)²)=N
N строится по оси ординат откладывается в относительных координатах отношение входного сопротивления к сопротивлению при резонансе, по оси абсцисс - относительная расстройка. При резонансе сопротивление контура чисто активное, минимальное, равное сопротивлению потерь. С увеличением расстройки возрастают реактивные составляющие и входное сопротивление возрастают.
Свойства резонанса в последовательном колебательном контуре.
Резонанс происходит на частоте собственных колебаний колебательного контура.
Сопротивление контура при резонансе чисто активное минимальное, равное сопротивлению потерь.
Падение напряжения на реактивных элементах равны между собой и в Q раз больше ЭДС источника питания.
UmLRп = UmСRп = QE
UmLRп = ImZВ = ZВE/ Rп = QE
ImRп = E/Rп
Резонансные кривые последовательного колебательного контура. Строится в относительных координатах. По оси абсцисс откладывается относительная расстройка, а по оси ординат отношение тока при расстройке к току при резонансе.
Ширина резонансной кривой зависит от добротности контура. Чем больше добротность, тем больше резонансная кривая. Полоса пропускания контура определяется на уровне 0,707 от максимума амплитуды (2∆0ω). На границе полосы пропускания резонансная кривая убывает в √2 раз.
1+Q² (2∆0ω/ω0)²
Q2∆0ω/ω0=1
2∆0ω=ω0/Q – ширина полосы пропускания.