1. Детали машин – это наука о назначении расчетов , устройстве и конструировании деталей машин.

2. Деталь-(от франц. detail - букв. - подробность), в технике - изделие,изготовленное без применения сборочных операций. Деталью называются такжеизделия, подвергнутые защитным или декоративным покрытиям или изготовленные из одного куска материала пайкой, склейкой, сваркой и т. п.

Маши́на (лат. machina — «механизм, устройство, конструкция», от др.-греч. μηχανή — «двигать») — техническое устройство, выполняющее механические движения для преобразования энергии, материалов и информации.

Сборочная единица (узел) - изделие или часть его (часть машины), составные части которого подлежат соединению между собой (собираются) на предприятии изготовителе (смежном предприятии). Сборочная единица имеет, как правило, определенное функциональное назначение.

3.

4.Вид напряжений:

Нормальное

-растяжение

-сжатие

-изгиб

Касательное

-среза

-кручения

6. Допускаемые напряжения – это наибольшие напряжения, которые можно допустить в конструкции при условии его безопасной, надежной и долговечной работы.

11. Шпоночные соединения предназначены для соединения с валами зубчатых колес, шкивов, маховиков, муфт и других деталей и служат для передачи крутящих моментов.

Клиновые шпонки (рис. 80, а) представляют собой клин с уклоном 1 : 100, который запрессовывается между валом и ступицей. Клиновые шпонки применяют при сборке узлов, не требующих высокой точности, так как они смещают ось ступицы по отношению к оси вала и при короткой ступице могут вызвать перекос.

Призматические шпонки (рис. 80, б) обеспечивают лучшее центрирование вала с сопрягаемой деталью и образуют как неподвижные, так и скользящие соединения. Призматические шпонки закладывают в шпоночные канавки так, чтобы между верхней гранью шпонки и дном канавки верхней детали был зазор

Направляющие шпонки (рис. 80, в) применяют в тех случаях, когда детали должны свободно перемещаться вдоль вала, например, кулачковая муфта, скользящие зубчатые колеса, ступицы конусных, дисковых муфт и т. д

Сегментные шпонки (рис. 80, г) работают так же, как и призматические, но применяют их только для неподвижных соединений.

Тангенциальные шпонки (рис. 80, д), как и клиновые, состоят из двух клиньев с уклоном 1:100.

12.Призматические шпонки рассчитывают на смятие, а в особо ответственных случаях проверяют на срез. При расчете принимают нагружение шпонки по длине равномерно. Условие прочности на смятие: откуда

Условие прочности сечения С-С на срез:

откуда

где [Мкр mах]- наибольший допускаемый крутящий момент, H м;

Мкр - крутящий момент на валу, Н м;

l - рабочая длина шпонки, мм;

d - диаметр вала, мм;

b и h - ширина и высота шпонки, мм;

К - выступ шпонки от шпоночного паза, мм;

[τср] - допускаемое напряжение на срез, МПа;

[σсм] - допускаемое напряжение на смятие, МПа;

В случае установки двух противоположно расположенных шпонок вводят поправочный коэффициент 0,75.

В машиностроении принимают

[σсм] = (0,3 ... 0,5) σт - для неподвижных соединений

и [σсм] = (0,1 ... 0,2 )σт - для подвижных соединений,

где σт - предел текучести материала шпонки.

13. Расчет по ГОСТ 21425 — 75. Этот уточненный расчет разработан пока только для прямобочных зубчатых соединений валов с зубчатыми колесами, муфтами и другими деталями, за исключением шкивов, паразитных шестерен и специальных соединений для компенсации перекоса или несоосности валов. Соединения шкивов и паразитных шестерен имеют иную схему нагружения и большие радиальные силы.При расчете по ГОСТу учитывают неравномерность распределения нагрузки по зубьям и длине зубьев (связанную с погрешностями изготовления и перекосами деталей от нагрузки), приработку рабочих поверхностей, срок службы и пр. Нагрузочная способность соединения определяется как меньшая из двух, полученных по расчету на смятие и на износ.Расчет на смятие предупреждает пластические деформации рабочих поверхностей зубьев при перегрузках. При записи расчетных формул принято все корректирующие коэффициенты учитывать при расчете допускаемых напряжений. При этом формулу (6.5) записывают в виде:

(Тем = 2T{zhd^l) ^ Ы, (6.6) Условие прочности болта

14. Условие прочности болта

http://alexfl.pro/inform/foto/raschet11.jpg

где

P - сила, действующая вдоль оси болта, Н;

d1 - внутренний диаметр резьбы, мм;

[σp] - допускаемое напряжение при растяжении (сжатии), МПа.

Пример расчета.

Определить диаметр нарезанной части хвостовика грузового крюка для силы Р=100.000 Н.

Гайку заворачивают, но не затягивают.

18.Механические передачи, применяемые в машиностроении, классифицируют (рис.1 и 2):

по принципу передачи движения:

- передачи трением (фрикционная — рис.1, а и ременная — рис.2, а);

- зацеплением (зубчатые — рис.1, б, червячные — рис.1, в; цепные — рис.2, б; передачи винт-гайка — рис.1, г, д);

Рис.1. Механические передачи с непосредственным контактом тел вращения:

а — фрикционная передача; б — зубчатая передача; в — червячная передача;

г, д — передачи винт-гайка

Рис.2. Передачи с гибкой связью: а — ременная; б — цепная

по способу соединения деталей:

- передачи с непосредственным контактом тел вращения (фрикционные, зубчатые, червячные, передачи винт-гайка — см. рис.1);

- передачи с гибкой связью (ременная, цепная — см. рис.2).

Кинематические схемы механических передач приведены на рис.3 и рис.4.Краткая характеристика этих передач (рис.3): передачи зубчатые цилиндрические между параллельными валами (а — с прямыми и косыми зубьями; б — с шевронными зубьями; в — внутреннего зацепления; г — реечные); передачи зубчатые конические между пересекающимися валами (д — с прямыми, косыми и круговыми зубьями; е — коническая — гипоидная); передачи зубчатые (цилиндрические) между скрещивающимися валами (ж — винтовая).

Механической передачей называют устройство для передачи механического движения от двигателя к исполнительным органам машины.

18. Передачи имеют широкое распространение в машиностроении по следующим причинам:

1) энергию целесообразно передавать при больших частотах вращения;

2) требуемые скорости движения рабочих органов машин, как правило, не совпадают с оптимальными скоростями двигателя; обычно ниже, а создание тихоходных двигателей вызывает увеличение габаритов и стоимости;

3) скорость исполнительного органа в процессе работы машины-орудия необходимо изменять (например, у автомобиля, грузоподъемного крана, токарного станка), а скорость машины-двигателя чаще постоянна (например, у электродвигателей);

4) нередко от одного двигателя необходимо приводить в движение несколько механизмов с различными скоростями;

5) в отдельные периоды работы исполнительному органу машины требуется передать вращающие моменты, превышающие моменты на валу машины-двигателя, а это возможно выполнить за счет уменьшения угловой скорости вала машины-орудия;

6) двигатели обычно выполняют для равномерного вращательного движения, а в машинах часто оказывается необходимым поступательное движение с определенным законом;

7) двигатели не всегда могут быть непосредственно соединены с исполнительными механизмами из-за габаритов машины, условий техники безопасности и удобства обслуживания.

Как правило, угловые скорости валов большинства используемых в настоящее время в технике двигателей (поршневых двигателей внутреннего сгорания, газотурбинных, электрических, гидравлических и пневматических двигателей) значительно превышают угловые скорости валов исполнительных или рабочих органов машин, порой на 2-3 порядка. Поэтому доставка (передача) энергии двигателя с помощью передачи любого типа, в том числе и механической, происходит, как правило, совместно с одновременным преобразованием моментов и угловых скоростей (в сторону повышения первых и понижения последних).

При этом необходимо отметить, что конструктивное обеспечение функции транспортного характера – чисто передачи энергии иной раз вступает в логическое противоречие с направлением задачи конечного преобразования силовых и скоростных параметров этой энергии. Например, в трансмиссиях многих транспортных машин (особенно высокой проходимости) входной редуктор сначала повышает частоту вращения, понижение ее до требуемых пределов производят бортовые или колесные редукторы.

Этот прием позволяет снизить габаритно-весовые показатели промежуточных элементов трансмиссии (коробок перемены передач, карданных валов) – размеры валов и шестерен пропорциональны величине передаваемого крутящего момента в степени 1/3.

Аналогичный принцип используется при передаче электроэнергии – повышение напряжения перед ЛЭП позволяет значительно снизить тепловые потери, определяемые в основном силой тока в проводах, а заодно уменьшить сечение этих проводов.

Иногда передача механической энергии двигателя сопровождается также преобразованием вида движения (например, поступательного движения во вращательное или наоборот) или законов движения (например, равномерного движения в неравномерное).

Широко известными образцами таких передач являются кривошипно-шатунный механизм и кулачковый привод механизма газораспределения.

Классификация механических передач

Механические передачи, применяемые в машиностроении, классифицируют (рис.1 и 2):

по принципу передачи движения:

- передачи трением (фрикционная — рис.1, а и ременная — рис.2, а)

- зацеплением (зубчатые — рис.1, б, червячные — рис.1, в; цепные — рис.2, б; передачи винт-гайка — рис.1, г, д);

Рис.1. Механические передачи с непосредственным контактом тел вращения:

а — фрикционная передача; б — зубчатая передача; в — червячная передача;

Рис.2. Передачи с гибкой связью: а — ременная; б — цепная

по способу соединения деталей:

- передачи с непосредственным контактом тел вращения (фрикционные, зубчатые, червячные, передачи винт-гайка — см. рис.1);

- передачи с гибкой связью (ременная, цепная — см. рис.2).

Кинематические схемы механических передач приведены на рис.3 и рис.4.

Краткая характеристика этих передач (рис.3): передачи зубчатые цилиндрические между параллельными валами (а — с прямыми и косыми зубьями; б — с шевронными зубьями; в — внутреннего зацепления; г —реечные); передачи зубчатые конические между пересекающимися валами (д — с прямыми, косыми и круговыми зубьями; е — коническая — гипоидная); передачи зубчатые (цилиндрические) между скрещивающимися валами (ж — винтовая).

В транспортном машиностроении, в многоцелевых гусеничных и колесных машинах зубчатые и червячные передачи в силу своих многих достоинств получили большое распространение. Это - трансмиссии основных танков российского производства, приводы поворота башен, трансмиссии БТР и автомобилей.

На рис.4, а показано схематичное изображение червячной передачи; 4, б — цепной передачи; 4, в — передачи винт-гайка; 4, г — ременной передачи.

Передачи гибкими связями широко применяются в общем машиностроении, наиболее типичными их представителями являются клиноременные передачи, обладающие многими достоинствами. В качестве наиболее широко распространенного примера таких передач можно привести приводы вентиляторов, генераторов, водяных насосов и компрессоров двигателей внутреннего сгорания.

Рис.3. Кинематические схемы механических передач: а — цилиндрические зубчатые передачи с внешним зацеплением; б — цилиндрические передачи с внутренним зацеплением; в — передача шестерня—рейка; г — конические зубчатые передачи с пересекающимися осями валов; д — гипоидная передача; е — передачи зубчатые цилиндрические со скрещивающимися валами

Рис.4. Кинематические схемы механических передач: а — червячная передача; б — цепная передача;

в — передача винт-гайка; г — ременная передача

Зубчатые передачи

Зубчатые передачи получили наибольшее распространение в машиностроении благодаря следующим достоинствам:

а) практически неограниченной передаваемой мощности,

б) малым габаритам и весу,

в) стабильному передаточному отношению,

г) высокому КПД, который составляет в среднем 0,97 - 0,98.

Недостатком зубчатых передач является шум в работе на высоких скоростях, который однако может быть снижен при применении зубьев соответствующей геометрической формы и улучшении качества обработки профилей зубьев.

При высоких угловых скоростях вращения рекомендуется применять косозубые шестерни, в которых зубья входят о зацепление плавно, что и обеспечивает относительно бесшумную работу. Недостатком косозубых шестерен является наличие осевых усилий, которые дополнительно нагружают подшипники. Этот недостаток можно устранить, применив сдвоенные шестерни с равнонаправленными спиралями зубьев или шевронные шестерни. Последние, ввиду высокой стоимости и трудности изготовления применяются сравнительно редко - обычно лишь для уникальных передач большой мощности. При малых угловых скоростях вращения применяются конические прямозубые шестерни, а при больших - шестерни с круговым зубом, которые в настоящее время заменили конические косозубые шестерни, применяемые ранее. Конические гипоидные шестерни тоже имеют круговой зуб, однако оси колес в них смещены, что создает особенно плавную и бесшумную работу. Передаточное отнесение в зубчатых парах колеблется в широких пределах, однако обычно оно равно 3 - 5.

Червячные передачи

Это передачи со скрещивающимися осями. Отличаются полностью бесшумной работой и большим передаточным отношением в одной паре, которое в среднем составляет 16 - 25. Серьезным недостатком червячных передач, ограничивающим их применение при значительных мощностях, является низкий КПД, обусловленный большими потерями на трение в зацеплении. Как следствие низкого КПД - при работе передачипод нагрузкой, выделяется большое количество тепла, которое надо отводить во избежание перегрева. Средние значения КПД первичной передачи составляют 0,7 -0,8.

Цепные передачи

Применяются при передаче вращения между, параллельными удаленными друг от друга валами. В настоящее время получили распространение два типа приводных цепей:

а) цепи втулочно-роликовые (типа Галя),

б) цепи зубчатые из штампованных звеньев (типа Рейнольдса).

Зубчатые цепи, благодаря относительно меньшему шагу, работают более плавно и бесшумно.

Недостатком цепных передач является сравнительно быстрый износ шарниров, способствующий вытяжке цепи и нарушению ее зацепления со звездочкой, а также шумная работа на высоких скоростях вследствие особенностей кинематики цепной передачи.

Ременные передачи

Применяются также для передачи вращения между параллельными удаленными валами. Область распространения этих передач в настоящее время значительно сократилась, однако они еще находят широкое применение в качестве первичного привода от двигателя, а также привода к механизмам, обладающим большим моментом вращающихся масс. При трогании с места и в случае внезапных перегрузок ремнипробуксовывают, спасая механизмы от поломок.

Преимущественное распространение перед плоскими получили плановые ремни, обладающие большей тяговой способностью.

Фрикционные передачи.

Фрикционные передачи по форме фрикционных катков могут быть: цилиндрическими, коническими, лобовыми - с внешним и внутренним контактом. Главное достоинство фрикционных передач заключается в возможности создания на их базе фрикционных вариаторов (бесступенчатых коробок передач), а также в бесшумной их работе при высоких скоростях. .

20. Классификация ременных передач:

1. По форме поперечного сечения ремня: плоскоременные (поперечное сечение ремня имеет форму плоского вытянутого прямоугольника, рис. 2.1.а); клиноременные (поперечное сечение ремня в форме трапеции рис. 2.1.б); поликлиноременные (ремень снаружи имеет плоскую поверхность, а внутренняя, взаимодействующая со шкивами, поверхность ремня снабжена продольными гребнями, выполненными в поперечном сечении в форме трапеции рис. 2.1.г); круглоременные (поперечное сечение ремня имеет форму круга рис. 2.1.в); зубчатоременная (внутренняя, контактирующая со шкивами, поверхность плоского ремня снабжена поперечными выступами, входящими в процессе работы передачи в соответствующие впадины шкивов).

2. По взаимному расположению валов и ремня: с параллельными геометрическими осями валов и ремнем, охватывающим шкивы в одном направлении – открытая передача (шкивы вращаются в одном направлении); с параллельными валами и ремнем, охватывающим шкивы в противоположных направлениях – перекрестная передача (шкивы вращаются во встречных направлениях); оси валов перекрещиваются под некоторым углом (чаще всего 90°) – полуперекрестная передача.

22. Силовые соотношения в ременной передаче. Необходимым условием нормальной работы любой фрикционной передачи, включая ременные, является наличие сил нормального давления между поверхностями трения. В ременной передаче такие силы возможно создать только за счет предварительного натяжения ремня. При неработающей передаче силы натяжения обеих ветвей будут одинаковыми (обозначим их F0, как на рис 2.3.а). В процессе работы передачи набегающая на этот шкив ветвь ремня за счет трения ведущего шкива о ремень получает дополнительное натяжение (обозначим силу натяжения этой ветви F1), в то время как вторая, сбегающая с ведущего шкива, ветвь ремня несколько ослабляется (её силу натяжения обозначим F2, см. рис. 2.3.б). Тогда, очевидно, окружное усилие, передающее рабочую нагрузку , но с другой стороны, как и для всякой передачи вращения (см. (2.8)), а для поступательно движущихся ветвей ремня можно записать , где P – мощность передачи, а Vp средняя скорость движения ремня. Суммарное натяжение ветвей ремня остается неизменным, как в работающей, так и в неработающей передаче, то есть . Но по формуле Эйлера для ремня, охватывающего шкив, , где – основание натурального логарифма (e » 2,7183), f – коэффициент трения покоя (коэффициент сцепления) между материалами ремня и шкива (табл. 2.1), a – угол охвата ремнем шкива (определен выше).

С учетом высказанных соображений и используя известные соотношения нетрудно получить зависимость для вычисления оптимальной величины сил предварительного натяжения ремня

а из последнего, выражая тяговое усилие на ведущем шкиве в соответствии с (2.8), получим

Рис. 2.3. Силы в ременной передаче.

где индексы «1» указывают на параметры, относящиеся к ведущему шкиву передачи. Если величину предварительного натяжения ремня сделать меньшей по сравнению с представленным в выражении (2.19), то произойдет буксование (проскальзывание) ремня, и переданная на выходной вал мощность уменьшится до величины, соответствующей фактическому значению силы предварительного натяжения. Если же силы предварительного натяжения ветвей будут больше оптимальной величины, необходимой для передачи заданной мощности, то возрастёт относительная доля мощности, затраченная на упругое скольжение ремня по шкивам, что также приведет к снижению мощности на выходном валу передачи, то есть к уменьшению её КПД.

Аналогично, сила натяжения ведущей ветви составит

Отношение разности сил натяжения в ветвях ремня работающей передачи к сумме этих сил называется коэффициентом тяги

Коэффициент тяги характеризует качество работы передачи. Его оптимальное значение нетрудно найти, используя выражение (2.18),

Как видно из последнего выражения оптимальная величина коэффициента тяги не зависит ни от передаваемой мощности, ни от предварительного натяжения ремня, а только лишь от свойств фрикционной пары материалов, из которых изготовлены ремень и шкив, и от конструктивных параметров передачи. Численные значения j0 для ремней из различных материалов и угла охвата ремнем стального ведущего шкива, равного 180°, пред­ставлены в табл. 2.1.

24. Как показано выше сила натяжения ведущей ветви ремня существенно превышает силу натяжения свободной ветви (F1>F2). Отсюда следует, что удлинение каждог

отдельно взятого элемента ремня меняется в зависимости от того, на какую его ветвь этот элемент в данный момент времени попадает. Изменение этой элементарной части ремня может происходить только в процессе ее движения по шкивам. При этом, проходя по ведущему шкиву (при переходе с ведущей ветви на свободную), эта элементарная часть укорачивается, а при движении по ведомому шкиву (переходя со свободной ветви ремня на его ведущую ветвь) – удлиняется. Изменение длины части ремня, соприкасающейся с поверхностью шкива, возможно только с её частичным проскальзыванием. Изложенные соображения позволяют сформулировать два важнейших следствия неодинаковой загрузки ведущей и холостой ветвей ремня:

Работа ременной передачи без скольжения ремня по рабочей поверхности шкивов невозможна.

Скорости движения ведущей и свободной ветвей ремня различны, а следовательно различны и скорости рабочих поверхностей ведущего и ведомого шкивов.

25. Тяговая способность и долговечность ремня являются основными критериями работоспособности ременной передачи. Проектный расчет ременной передачи обычно выполняется по тяговой способности, а расчет долговечности при этом является проверочным. Проиллюстрируем поведение ременной передачи графиком, на котором по оси абсцисс отложен коэффициент тяги, а по оси ординат - коэффициент скольжения и КПД (рис. 2.4). На графике можно выделить три основных зоны:

В зоне упругого скольжения коэффициент скольжения растет линейно с увеличением коэффициента тяги, одновременно возрастает и КПД передачи, достигая максимального значения при оптимальной величине коэффициента тяги j0. Дальнейшее увеличение коэффициента тяги приводит к частичному буксованию ремня, коэффициент скольжения растет нелинейно и намного интенсивнее по сравнению с 1 зоной, а КПД также нелинейно и интенсивно снижается. При достижении коэффициентом тяги величины jmax наступает полное буксование передачи (ведомый шкив останавливается), величина скольжения становится равной единице, а КПД падает до нулевого значения.

Представленный выше анализ показывает, что наиболее благоприятной для работы передачи является область коэффициентов тяги, прилегающая к его оптимальному значению, поскольку именно в этой области передача обладает максимальным КПД. При этом величина упругого скольжения для разных типов ремней лежит в пределах 1…2%, а КПД для передачи плоским ремнем можно принять равным 0,95…0,97, клиновым или поликлиновым – 0,92…0,96.

Напряжения в ремне. Напряжения, возникающие в ведущей ветви ремня от действия рабочих нагрузок, нетрудно определить, разделив (2.20) на площадь поперечного сечения ремня Aр,

Кроме рабочих напряжений, обусловленных предварительным натяжением ремня и тяговым усилием, участвующем в передаче мощности от ведущего шкива к ведомому, в ремне возникают еще два вида дополнительных напряжений – изгибные и центробежные.

Изгибные напряжения возникают при изгибе ремня в момент огибания им шкивов, при этом наибольшая величина изгибных напряжений соответствует меньшему радиусу изгиба, то есть максимальные напряжения изгиба возникают в ремне при обегании меньшего (чаще всего являющегося ведущим) шкива. Учитывая последнее, на основе формул сопротивления материалов получаем

Модуль упругости материала некоторых ремней

Тип ремня

Модуль упругости E, МПа

Резинотканевый 200…300

Капроновый 600

Клиновой:

Кордтканевый

кордшнуровой

250…400 500…600

где E – модуль упругости материала ремня (см. табл. 2.3), y0 – расстояние от нейтрального слоя до наружного (растянутого) волокна ремня, D1 – диаметр наименьшего шкива передачи. Принимая для плоского ремня y0 = d / 2, где d - толщина ремня, а для клинового - y0 = (0,25…0,38)h, где h – толщина ремня, получаем:

Таким образом, напряжения изгиба пропорциональны толщине ремня и обратнопропорциональны диаметру наименьшего из шкивов, работающих в передаче.Часть ремня, прилегающая к шкиву участвует в круговом движении, что обусловливает действие на неё центробежных сил, вызывающих в ремне растягивающие напряжения. Напряжения от центробежных сил можно вычислить по простому соотношению

Как видим, напряжения, вызванные в ремне действием центробежных сил, квадратично зависят как от частоты вращения наименьшего шкива, так и от его диаметра.

На внешней стороне ремня все три вида названных напряжений являются растягивающими и потому суммируются. Таким образом, максимальные растягивающие напряжения в ремне

Анализ реальных передач показывает, что напряжения от изгиба sи и от действия центробежных сил sц обычно сравнимы и часто даже превосходят по величине напряжения от рабочей нагрузки sр. При этом следует учитывать, что увеличение sи не способствует повышению тяговой способности передачи, с другой стороны, эти напряжения, периодически меняясь, являются главной причиной усталостного износа ремней.

Расчет ременных передач основан на общей теории ременных передач и экспериментальных данных. При этом формула Эйлера и зависимость (2.31) непосредственно не используются, а влияние дополнительных напряжений sи и sц на долговечность передачи учитывают при выборе её геометрических параметров (a, D1, a и др.) и допускаемых напряжений [st]0 и [st], используемых в расчете.

При проектном расчете диаметр малого шкива D1 можно оценить по модифицированной формуле М.А. Саверина

малом шкиве и скорость движения ремня (уменьшение сцепления центробежными силами), на режим работы передачи.

Обычно такой расчет предполагает минимальный срок службы передачи (ремня) 2000 ч. Однако, экспериментально установлено, что для ремней не удается установить предел неограниченной выносливости, а ресурс ремня, выраженный числом пробегов за срок службы N, связан с наибольшим напряжением, вычисленным по зависимости (2.31), соотношением.

27.

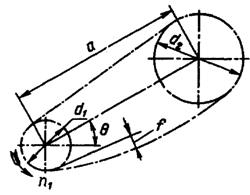
Основные геометрические соотношения в цепной передаче (рис. 3.3). Как указывалось выше, главным геометрическим параметром цепи и цепной передачи в целом является шаг t между осями шарниров цепи, равный расстоянию между центрами впадин между зубьями звездочек. Межосевое расстояние передачи выбирается в зависимости от шага цепи по следующему соотношению

. (3.1 ) .В этом выражении меньшие значения коэффициента в правой части соответствуют меньшим передаточным числам и наоборот.

Делительный диаметр d звездочки (диаметр окружности на которой лежат оси шарниров цепи, охватывающей звездочку) также зависит от шага цепи t

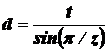, (3.2)

где z –число зубьев звездочки.

В свою очередь число зубьев меньшей звездочки (её параметрам присвоим индекс «1») выбирают по эмпирическим соотношениям:

для роликовых и втулочных цепей

при условии z1 ³ 13; (3.3)

для зубчатых цепей

при условии z1 ³ 17; (3.4)

где u – передаточное число.

Число зубьев большей звездочки с округлением до ближайшего большего нечетного числа. При этом рекомендуется принимать число зубьев большей звездочки не более 120 для роликовых и втулочных цепей и не более 140 для зубчатых цепей.

Длину цепи Lр, выраженную в шагах (число звеньев цепи), для известного межосевого расстояния a можно вычислить по выражению

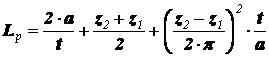. (3.5)

Полученное по выражению (3.5) значение необходимо округлить до ближайшего целого четного числа. При четном числе звеньев цепи и нечетных числах зубьев звездочек будет обеспечен наиболее равномерный износ как самих звездочек, так и шарниров цепи.

Далее по выбранному числу звеньев цепи необходимо уточнить межосевое расстояние передачи

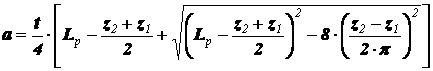. (3.6)

Полученное расчетом по (3.6) значение межосевого расстояния с целью исключения перенатяжения цепи из-за неточностей изготовления и монтажа сокращают на 0,2…0,4%, так чтобы свободная (ведомая) ветвь цепи имела некоторое провисание f (рис. 3.3). Для передачи, у которой угол q наклона межосевой линии к горизонту не превышает 40°, величина провисания ведомой ветви цепи , а для передач с углом -