Конструкции моп - транзисторов в сбис

Наиболее распространённой конструкцией МОП - транзистора, используемой более 10 лет в полупроводниковой промышленности, является LDD (Lightly Doped Drain) структура (рисyнок 5.1). Её особенностью является наличие мелких слаболегированных областей, которые удлиняют области истока и стока в сторону канала. Концентрацию легирующей примеси в этих областях (фосфор и бор) и режим её разгонки выбирают таким образом, чтобы получить плавный p-n-переход. Полученное таким способом снижение напряжённости электрического поля в канале на границе со стоком уменьшает энергию горячих электронов, которые вызывают долговременную деградацию параметров транзистора.

Слаболегированные LDD-области также повышают напряжение прокола, инжекционного и лавинного пробоя транзистора и эффект модуляции длины канала.

Глубина LDD-областей истока и стока составляет 50–100 нм для транзисторов с длиной канала 0,25 мкм. Уменьшение глубины p-n-переходов до 10 нм приводит к увеличению сопротивления слоёв истока и стока до 10 кОм, что ограничивает нагрузочную способность транзистора. Перекрытие LDD-областей затвором должно быть не менее 15–20 нм, чтобы предотвратить снижение нагрузочной способности транзистора. Толщина поликремниевого затвора составляет порядка 300 нм.

Для снижения емкостей транзистора выбирают слаболегированную подложку, а для обеспечения необходимого порогового напряжения и снижения напряжения прокола применяют легирование канала примесью того же типа, что и в подложке. Легирование выполняют примерно на глубину области пространственного заряда под затвором.

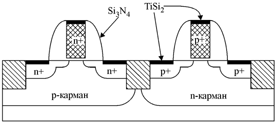
Контакты к областям истока, стока и к поликремниевому затвору выполняют с промежуточным формированием слоя TiSi₂ или CoSi₂ толщиной порядка 40 нм, что обеспечивает удельное сопротивление около 5 Ом. Изоляция между поликремниевым затвором и контактами к истоку и стоку выполняется в виде спейсера (разграничителя) (рис. 5.1) из Si₃N₄.

Концентрация примеси в канале составляет ~5*10¹⁷ см^-3. Увеличение концентрации примеси свыше этого значения, необходимое для транзисторов с длиной канала менее 100 нм, ведёт к появлению туннелирования электронов через р - n - переходы истока и стока.

Для формирования карманов МОП - транзисторов разного типа проводимости (рис. 5.3) используют фосфор и бор. Изоляцию между карманами выполняют обычно мелкими канавками, стенки которых окисляют, а внутренность заполняют поликремнием.

Базовая тория кулоновской блокады.

Одноэлектроника — это раздел наноэлектроники, изучающий условия и приборные структуры, в которых перенос тока осуществляется одним электроном, или, точнее, определяется движением одного электрона.

В принципе в современных МОП-транзисторах с малой длиной и шириной канала, например в КНИ-МОП-транзисторах с длиной канала , толщиной канала и шириной канала , перенос тока в определенные моменты времени осуществляется одним или считанным числом электронов. Число электронов, образующих ток, очевидно равно , где – концентрация электронов. Для =0.1 мкм, = 0.01мкм, =0.01 мкм и традиционной для проводящего канала МОП-транзистора =10²⁴ м^–3 имеем 10.

Однако в стандартном МОП-транзисторе электроны движутся непрерывно, нет возможности выделить один электрон из общего потока и потому данные транзисторы не рассматриваются как приборы одноэлектроники.

Теория одноэлектронного туннелирования впервые предложена К.К. Лихаревым..

Рассмотрим теорию Лихарева подробно. Первой была описана система из одного туннельного перехода между двумя металличе­скими контактами. Пусть емкость такой системы есть С. Тогда энергия данной системы, т. е. по сути конденсатора, составляет

E=Q²/2C, (1)

Где Q - заряд на обкладках конденсатора. Так как заряд электро­на - дискретная величина, минимальное значение изменения энер­гии ΔЕ составит

ΔE=e²/2C (2)

где е - элементарный заряд электрона. Для наблюдения эффектов необходимо, чтобы минимальное изменение энергии было больше т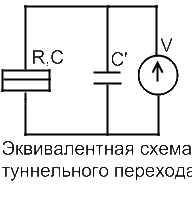 емпературных флуктуаций, т.е.

ΔЕ >> к₀Т, (3)

где к - постоянная Больцмана, а Т - температура. Кроме того, не­обходимо, чтобы данное изменение превышало квантовые флук­туации

ΔЕ>>hG/C (4)

где G = max(G_S,G_I), G_I - проводимость туннельного перехода, G_S - проводимость, шунтирующая переход. Исходя из (9.1.4) можно записать

G<<R_Q^-1 (5)

где Rq = h/4e² << 6.45 кОм - квантовое сопротивление.

Одно из важнейших предположений теории одноэлектронного туннелирования состоит в том, что начальный заряд Q₀ на тун­нельном переходе может быть отличен от нуля и более того может принимать значения, не кратные целому числу электронов. Дан­ный факт объясняется тем, что начальный заряд может создаваться поляризацией близлежащих электродов, заряженных примесей и т.д. и, таким образом, может иметь любое значение. Тогда в урав­нении (9.1.1) Q = Qo - е. Из всего вышесказанного вытекает, что если Q лежит в пределах от -е/2 до +е/2, добавление или вычита­ние целого числа электронов будет увеличивать энергию (1), т. е. энергетически невыгодно.

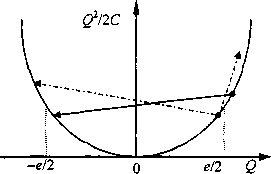
Данный вывод иллюстрируется рис. 9.1, из которого видно, что если заряд хотя бы немного меньше зна­чения е/2, то добавление или вычи­тание одного электрона (штрих- пунктирные стрелки) приводит к увеличению общей энергии. Если заряд превышает значение е/2, то выгодным становится туннелирова­ние электрона через диэлектрик. Так как напряжение на конденсаторе V = Q/С, при напряжениях от -е/(2С) до +е/(2С) ток через туннельный переход протекать не должен. Дру­гими словами, для того чтобы обеспечить туннелирование через переход, необходимо преодолеть силу кулоновского отталкивания электронов. Данный эффект отсутствия тока при приложении на­пряжения в указанных пределах был назван эффектом кулонов­ской блокады.

Таким образом, кулоновская блокада - это явление отсутст­вия тока при приложении напряжения к туннельному переходу из-за невозможности туннелирования электронов вследствие их кулоновского отталкивания. Напряжение, которое необходимо приложить к переходу для преодоления кулоновской блокады

V_КБ~ е/(2С), (6)

иногда называют напряжением отсечки. В дальнейшем мы будем придерживаться термина «напряжение кулоновской блокады» и обозначения V_КБ .

Одиночный тун­нельный переход

Рассмотрим процесс протекания тока через одиночный тун­нельный переход. Так как ток - величина непрерывная, заряд на одной стороне перехода накапливается постепенно. При достиже­нии величины е/2 происходит туннелирование одного электрона через переход и процесс повторяется. Это аналогично падению капель из неплотно закрытого крана: по достижении некоторой критической массы капля отрывается от крана и начинается обра­зование следующей. Заряд одного электрона е накапливается при токе I за время t. е = I*t, затем электрон туннелирует через переход. Нетрудно ви­деть, что процесс повторяется периодически с частотой

f = I/e (7)

где I - ток через переход. Такие осцилляции были названы одно­электронными туннельными осцилляциями.

Еще раз отметим, что наблюдение кулоновской блокады воз­можно лишь при выполнении условий (3) и (5). Эти усло­вия, особенно температурное (3), накладывают жесткие ограничения на конструкции одноэлектронных приборов. Из (2) и (3) можно получить значение емкости, необходимое для наблюдения кулоновской блокады при данной температуре Т: С << е²/(2к₀Т). (8)

Подставив в формулу (8) численные значения е и к, получим, что для наблюдения эффекта при 4.2 К необходима емкость много меньше 10^-16 Ф, а для Т — 77 К и Т= 300 К соответственно много меньше 10^-17 и 10^-18. Таким образом, для работы приборов при высоких температурах (выше 77 К) необходима емкость 10^-18.. .10^-19 Ф.

На рис. 9.2. показана эквивалентная схе­ма рассмотренной системы. Прямоугольни­ком обозначен туннельный переход. Такое графическое обозначение для кулоновского туннельного перехода общепринятое. Пере­ход характеризуется сопротивлением R и емкостью С, С’ – емкость подводящих кон­тактов.. К переходу приложено напряжение V. Из приведенной схемы видно, что если паразитная емкость С' больше емко­сти перехода, емкость системы будет определяться этой шунтирующей емкостью С'. В реальных приборах не удается получить шунтирующую емкость менее 10^-15 Ф, что как минимум на два порядка больше требуемой для наблюдения одно­электронного туннелирования даже при температурах жидкого гелия.

Таким образом, наблюдение одноэлектронного туннелирования в системе с одним переходом при современном развитии технологии является проблемой.

Два последовательных перехода.

Чтобы избежать влияние паразитных емкостей для хранения заряда одного электрона используют два последовательно включенных конденсатора.

Эквивалентная схема этой конструкции приведена на рис. 9.3.

В этом случае суммарная емкость системы будет , где и . Так как емкости конденсаторов намного меньше паразитных, то они и будут определять и , а значит и .

Выражение для общей электростатической энергии такой системы можно представить в виде

E=Q₁²/2C₁ + Q₂²/2C₂, (9)

где индексы соответствуют номерам переходов. Физически такая конструкция представляет собой малый проводник, отделенный туннельными переходами от контактов, поэтому Q₁ = Q₂ = Q - заряду, находящемуся на проводнике. Тогда (9) мож­но переписать в виде

E = Q²/2C_Σ, (10)

^Л0)

аналогично формуле (1), за исключением того, что вместо емко­сти С фигурирует суммарная емкость двух переходов C_Σ = С₁+С₂, так как С_\ и С2 включены параллельно, если смотреть с проводника. Таким образом, справедливыми остаются формулы (2), (4) и (8) при замене в них С на C_Σ . В формулах (3) и (4) необ­ходимо G заменить на max (G₁, G₂).