Числовые ряды

Приведем признаки сходимости числовых рядов:

а) интегральный признак Коши сходимости ряда 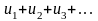с положительными членами. Если 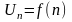, где 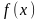- убывающая непрерывная функция, то ряд и интеграл 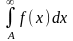сходятся или расходятся одновременно (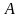 -некоторое число, );

б) признак Даламбера. Пусть 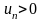(начиная с некоторого члена ряда) и существует предел

.

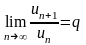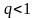Тогда ряд сходится, если , и расходится, е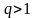сли . Если 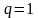, вопрос о сходимости ряда остается открытым;

в) признак Коши. Пусть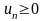 (начиная с некоторого члена ряда) и существует предел

.

Тогда ряд сходится, если , и расходится, если . В случае, когда , вопрос о сходимости ряда остается открытым;

г) первый признак сравнения. Если 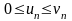(начиная с некоторого 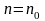), то из сходимости ряда следует сходимость ряда , а из расходимости ряда следует расходимость ряда ;

д) второй признак сравнения. Если существует конечный и отличный от нуля предел

,

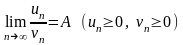то ряды и сходятся или расходятся одновременно;

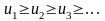е) признак Лейбница. Ряд с чередующимися знаками сходится, если и .

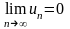Отметим еще необходимое условие сходимости ряда: Для того, чтобы ряд сходился, необходимо, чтобы .

Пример. Исследовать сходимость числового ряда .

Решение. Применим интегральный признак. Ясно, что функция 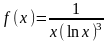будет непрерывной при 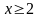и убывающей, при этом .

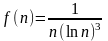Рассмотрим интеграл

.

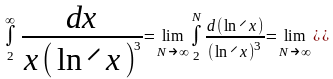Так как этот интеграл сходится, то сходится и ряд.

Пример. Исследовать сходимость числового ряда .

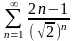Решение. Применим признак Даламбера. Очевидно, что

, ,

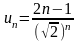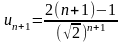тогда

т.к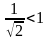 , то ряд сходится.

Пример. Исследовать сходимость числового ряда .

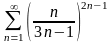Решение. Для решения вопроса о сходимости этого ряда используем признак Коши

,

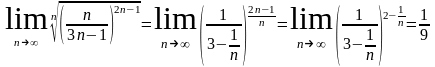т.к. 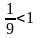, то ряд сходится.

Пример. Исследовать сходимость числового ряда .

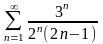Решение. Воспользуемся признаком Даламбера. = = =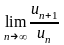

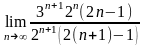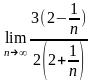т.к. , то ряд расходится.

Пример. Исследовать сходимость числового ряда .

Решение. Легко видеть, что для этого ряда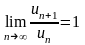 , т.е. признак Даламбера не дает ответа на вопрос о его сходимости. Воспользуемся первым признаком сравнения. Так как

и ряд сходится (см. сходимость обобщенного гармонического ряда ), то и наш ряд сходится.

Можно было бы воспользоваться вторым признаком сравнения. Сравним наш ряд с тем же рядом . Так как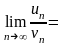 = =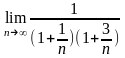1

то из сходимости ряда следует сходимость нашего ряда.

Функциональные ряды

Пример. Найти интервал сходимости степенного ряда

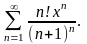
Решение. Пусть дан степенной ряд 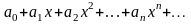. Число есть радиус сходимости степенного ряда, если при ряд сходится, а при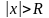 - расходится. Интервалом сходимости называют интервал . Известно, что радиус сходимости степенного ряда вычисляется по формуле

Воспользовавшись этой формулой, вычислим радиус сходимости нашего степенного ряда

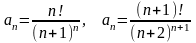и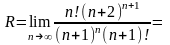

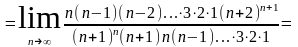
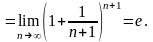
_{Итак, радиус сходимости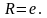} Следовательно, интервалом сходимости нашего ряда будет