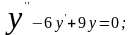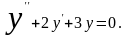- •Контрольная работа по дисциплине «Дополнительные главы математики» для студентов второго курса направления «Менеджмент» (заочной формы обучения)
- •Волгодонск
- •Рекомедации по выполнению контрольной работы
- •Контрольная работа на тему: Дифференциальные уравнения. Теория рядов.
- •Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Числовые ряды
- •Функциональные ряды
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Для
решения линейного однородного
дифференциального уравнения второго
порядка с постоянными коэффициентами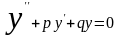 составляется
соответствующее характеристическое
уравнение:
составляется
соответствующее характеристическое
уравнение: .
.
Если корни
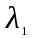 и
и
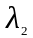 характеристического уравнения
действительны и различны, то общее
решение однородного уравнения будет
иметь вид:
характеристического уравнения
действительны и различны, то общее
решение однородного уравнения будет
иметь вид:
 .
.
Если и действительны и равны между собой, т.е.
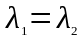 ,
то общее решение запишется в виде
,
то общее решение запишется в виде
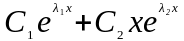 .
.Если корни являются комплексными числами
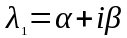 ,
,
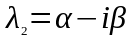 ,
то общее решение представляется в виде
,
то общее решение представляется в виде
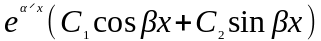 .
.
Пример. Найти общие решения уравнений:
|
|
|
|
|
|
|
|
|
Решение.
а) Составим
соответствующее характеристическое
уравнение и решим его: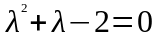 ,
,
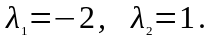 Согласно
сказанному выше, общее решение можно
записать в виде
Согласно
сказанному выше, общее решение можно
записать в виде
 .
.
b) Составляем
характеристическое уравнение ,
,
 .Отсюда
.Отсюда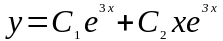 .
.
c) Характеристическое
уравнение имеет решение
имеет решение .
.
Следовательно,

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общее решение
линейного неоднородного дифференциального
уравнения
можно записать в виде
 где
где
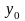 - общее решение соответствующего
однородного дифференциального уравнения,
а Y
- частное решение данного неоднородного
уравнения.
- общее решение соответствующего
однородного дифференциального уравнения,
а Y
- частное решение данного неоднородного
уравнения.
Функция Y может быть найдена методом неопределенных коэффициентов в следующих простейших случаях:
1)
 , где
, где
 многочлен
степени
.
многочлен
степени
.
Если
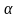 не является корнем характеристического
уравнения, то частное решение ищут в
виде
не является корнем характеристического
уравнения, то частное решение ищут в
виде
 ,
где
,
где
 многочлен степени
с неизвестными коэффициентами.
многочлен степени
с неизвестными коэффициентами.
Если - корень характеристического уравнения кратности
 ,
то
,
то
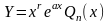 .
.
2)
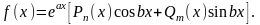
Если
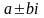 не
является корнем характеристического
уравнения, то полагают
не
является корнем характеристического
уравнения, то полагают
 ,
,
где
 многочлены
степени
многочлены
степени
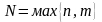 .
.
Если
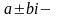 корни
характеристического уравнения кратности
(для уравнений второго порядка
корни
характеристического уравнения кратности
(для уравнений второго порядка
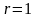 ),
то полагают
),
то полагают
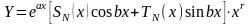 .
.
Функцию,
находящуюся в правой части линейного
неоднородного дифференциального
уравнения с постоянными коэффициентами,
имеющую вид

принято называть специальной правой частью.
Пример. Найти общее решение уравнения
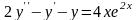 .
.
Решение.
Найдем
общее решение
однородного
дифференциального уравнения
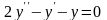 .
Характеристическое уравнение
.
Характеристическое уравнение
 имеет корни
имеет корни
 .
Следовательно,
.
Следовательно,
 .
.
Правая
часть уравнения равна
 .
Следовательно,
.
Следовательно,
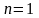 ,
и поскольку
,
и поскольку
 не является корнем характеристического
уравнения, то
не является корнем характеристического
уравнения, то
 .
Поэтому частное решение ищем в виде
.
Поэтому частное решение ищем в виде
 .
.
Дифференцируя Y два раза и подставляя производные в данное уравнение, получим

Сокращая
на
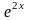 и приравнивая коэффициенты при одинаковых
степенях
и приравнивая коэффициенты при одинаковых
степенях
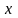 левой и правой частей последнего
равенства, находим:
левой и правой частей последнего
равенства, находим:
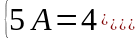
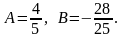
Отсюда
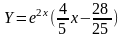 .
Значит, общее решение данного уравнения
имеет вид
.
Значит, общее решение данного уравнения
имеет вид
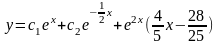 .
.
Пример.
Найти общее решение уравнения
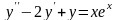 .
.
Решениe.
Найдем общее решение
 однородного дифференциального уравнения
однородного дифференциального уравнения
 .
.
Характеристическое
уравнение
 имеет корни
имеет корни
 (кратность корня
(кратность корня
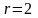 ).
Следовательно,
).
Следовательно,
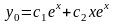 .
.
Правая
часть уравнения имеет вид
 .
Тогда
.
Тогда
 .
Так как
.
Так как
 совпадает с корнем
совпадает с корнем
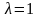 кратности
,
то частное решение ищем в виде
кратности
,
то частное решение ищем в виде
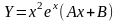 .
.
Дифференцируя
Y
два раза, подставляя в уравнение и
приравнивая коэффициенты, получим:
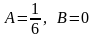 .
.
Общее решение данного уравнения имеет вид