2.3 Растяжение под действием сил тяжести

Собственный вес материала конструкций является внешней нагрузкой, распределенной по объему.

В машиностроении, как правило, влияние собственного веса не учитывается, так как машиностроительные детали имеют сравнительно небольшие размеры, при которых влияние собственного веса невелико.

В строительных конструкциях и сооружениях собственный вес является одной из основных нагрузок. Также надо учитывать собственный вес при расчете канатов шахт подъемников, штанг бурильных устройств, тросов воздушного заграждения и др.

Прямой стержень постоянного сечения F нагружен на свободном конце силой Р (рисунок 2.3). Удельный вес материала – γ.

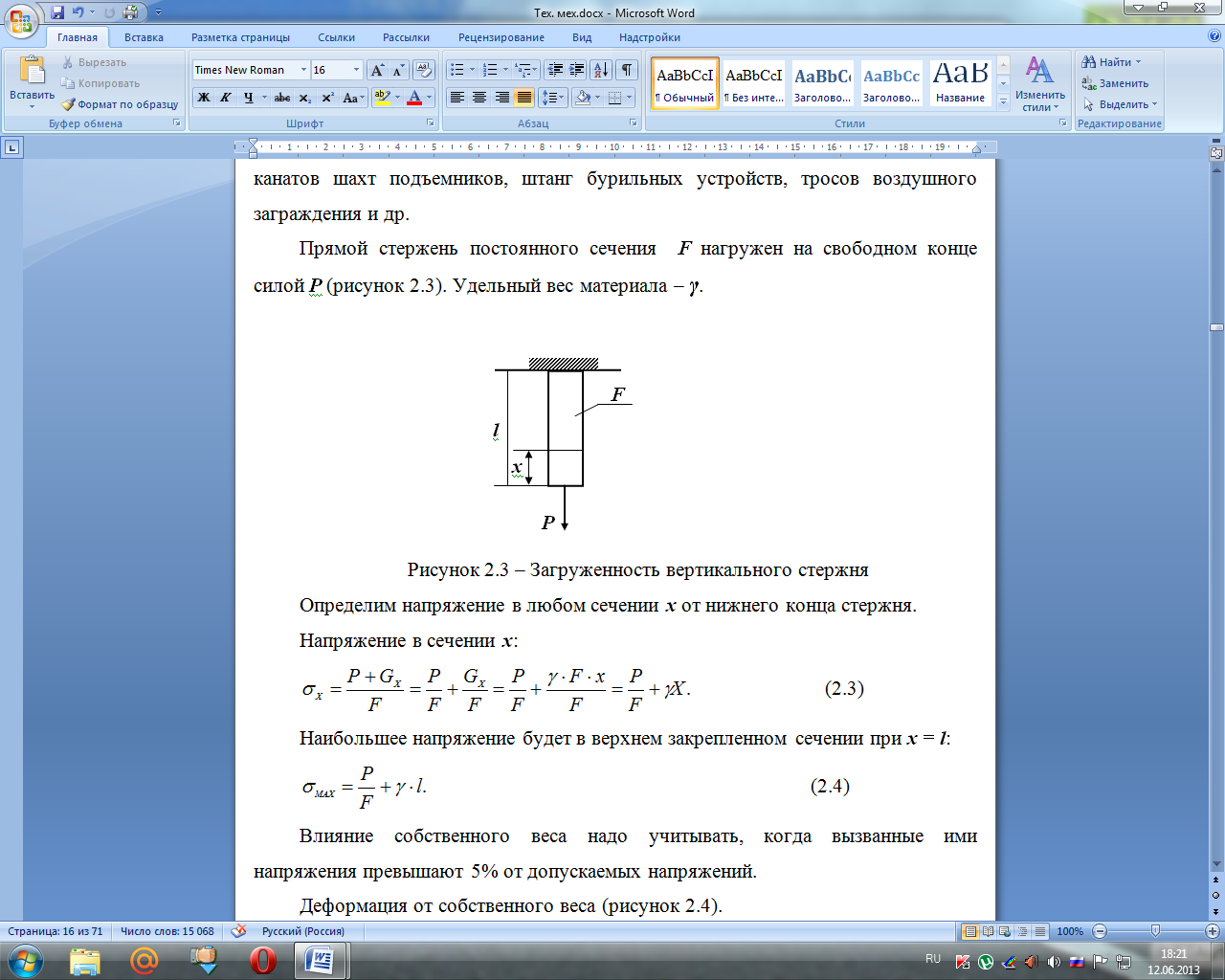
Рисунок 2.3 – Загруженность вертикального стержня

Определим напряжение в любом сечении x от нижнего конца стержня.

Напряжение в сечении x:

(2.3)

Наибольшее напряжение будет в верхнем закрепленном сечении при x = l:

(2.4)

Влияние собственного веса надо учитывать, когда вызванные ими напряжения превышают 5% от допускаемых напряжений.

Деформация от собственного веса (рисунок 2.4).

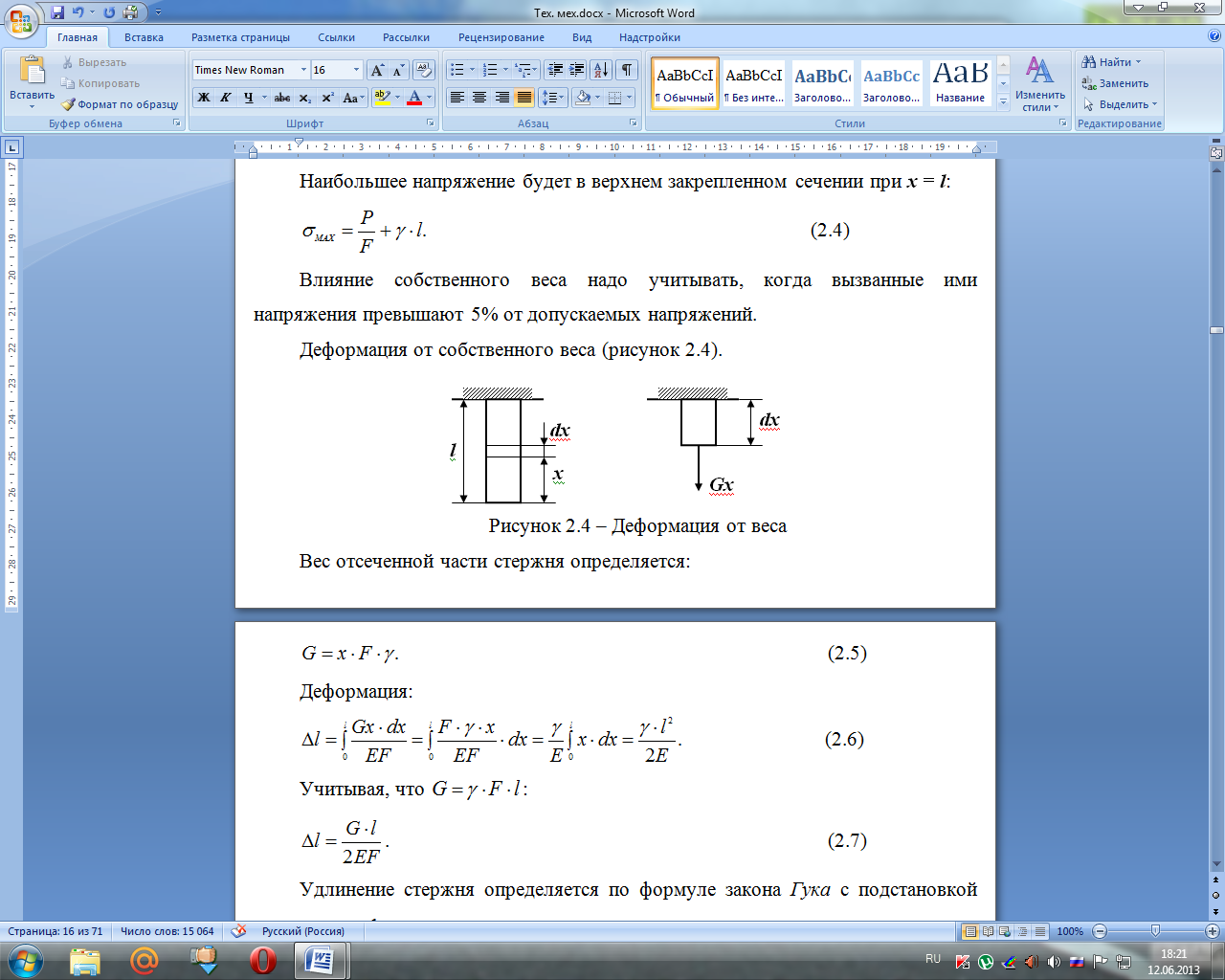
Вес отсеченной части стержня определяется:

(2.5)

Деформация:

(2.6)

Учитывая, что :

. (2.7)

Удлинение стержня определяется по формуле закона Гука с подстановкой вместо силы .

2.4 Эпюры продольных сил, напряжений и перемещений

Эпюры – это графики или диаграммы изменения некоторых величин в заданном направлении (обычно вдоль оси бруса). Они строятся для того, чтобы выявить наиболее опасные сечение бруса и напряжения в этом сечении.

Построим эпюры продольных сил, нормальных напряжений и перемещений в буквенном выражении (рисунок 2.5).

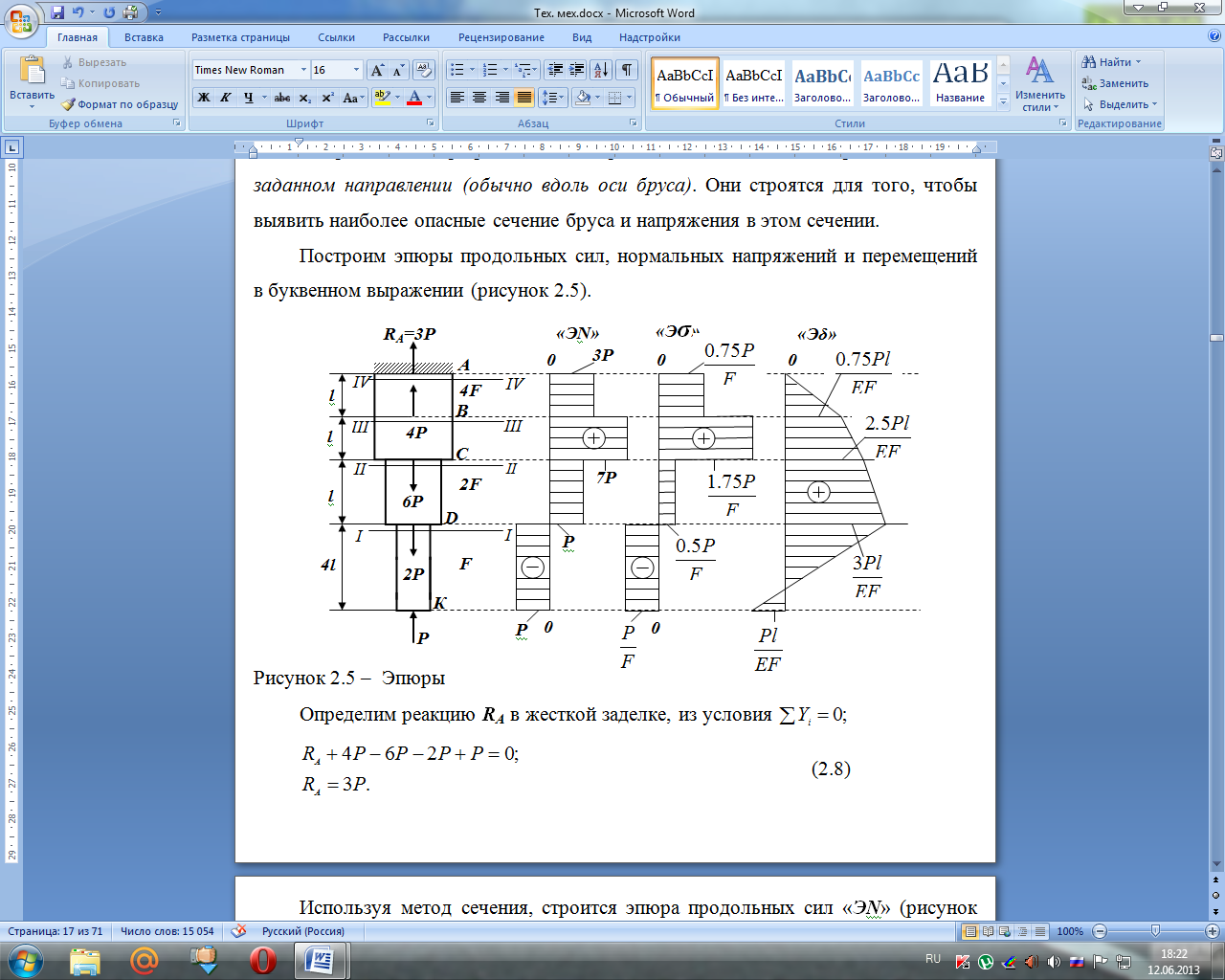
Рисунок 2.5 – Эпюры

Определим реакцию R_A в жесткой заделке, из условия

спользуя метод сечения, строится эпюра продольных сил «ЭN» (рисунок 2.5).

Напряжения определяются по формуле:

(2.9)

где - напряжение, продольная сила и площадь поперечного сечения i- го участка.

Строится эпюра напряжений «Эσ» (рисунок 2.5).

Перемещения определяются по формуле:

где l_i – длина i– го участка.

(2.11)

Строится эпюра перемещений «Эδ» (рисунок 2.5).

Вывод: 1. Наиболее напряженным является участок III.

2. Концевое сечение смещается вверх на величину

19.

Механические характеристики прочности материалов

• Технологический процесс

• Термообработка (термическая)

• Наклёп – обработка металла на холодную

• Температура, интенсивность, время нагружения.

Предел прочности - наибольшие напряжения, до которого деформации прямо пропорциональны напряжениям (рисунок 3.4).

Предел упругости - это такие напряжения, при котором материал не получает остаточных деформаций ( вернее они очень малы в пределах 0,001 – 0,005 % первоначальной длины образца), практически и почти совпадают (рисунок 3.4).

Предел текучести - напряжение, при котором деформации растут без заметного увеличения нагрузки (рисунок 3.4).

Предел прочности или временное сопротивление - наибольшее напряжение, которое может выдержать материал при растяжении (в точке С) (рисунок 3.4).

Для материалов, не имеющих площадки текучести, в качестве предела текучести принимаются напряжения, при котором остаточные деформации составляют 0,2 или 0,3 % первоначальной длины.

20.

Деформация растяжения