8.1 Дифференциальные уравнения поступательного движения

При поступательном движении твёрдого тела все его точки движутся так же, как и его центр масс. Поэтому дифференциальные уравнения движения центра масс тела являются дифференциальными уравнениями поступательного движения твёрдого тела.

(8.1)

где m – масса тела;

, , - координаты центра масс тела;

- проекции внешней силы на оси координат;

, , - проекции главного вектора внешних сил на эти оси.

По дифференциальным уравнениям поступательного движения можно решать два основных типа задач на поступательное движение твёрдого тела:

• по заданному движению твёрдого тела определять главный вектор, приложенный к нему внешних сил;

• по заданным внешним силам, действующим на тело, и начальным условиям движения, находить кинематические уравнения движения тела, если известно, что оно движется постоянно.

15.

Дифференциальное уравнение вращения твёрдого тела

Рассмотрим твёрдое тело, вращающееся вокруг неподвижной оси Z c угловой скоростью . Вычислим кинетический момент этого тела относительно оси его вращения (рисунок 8.1).

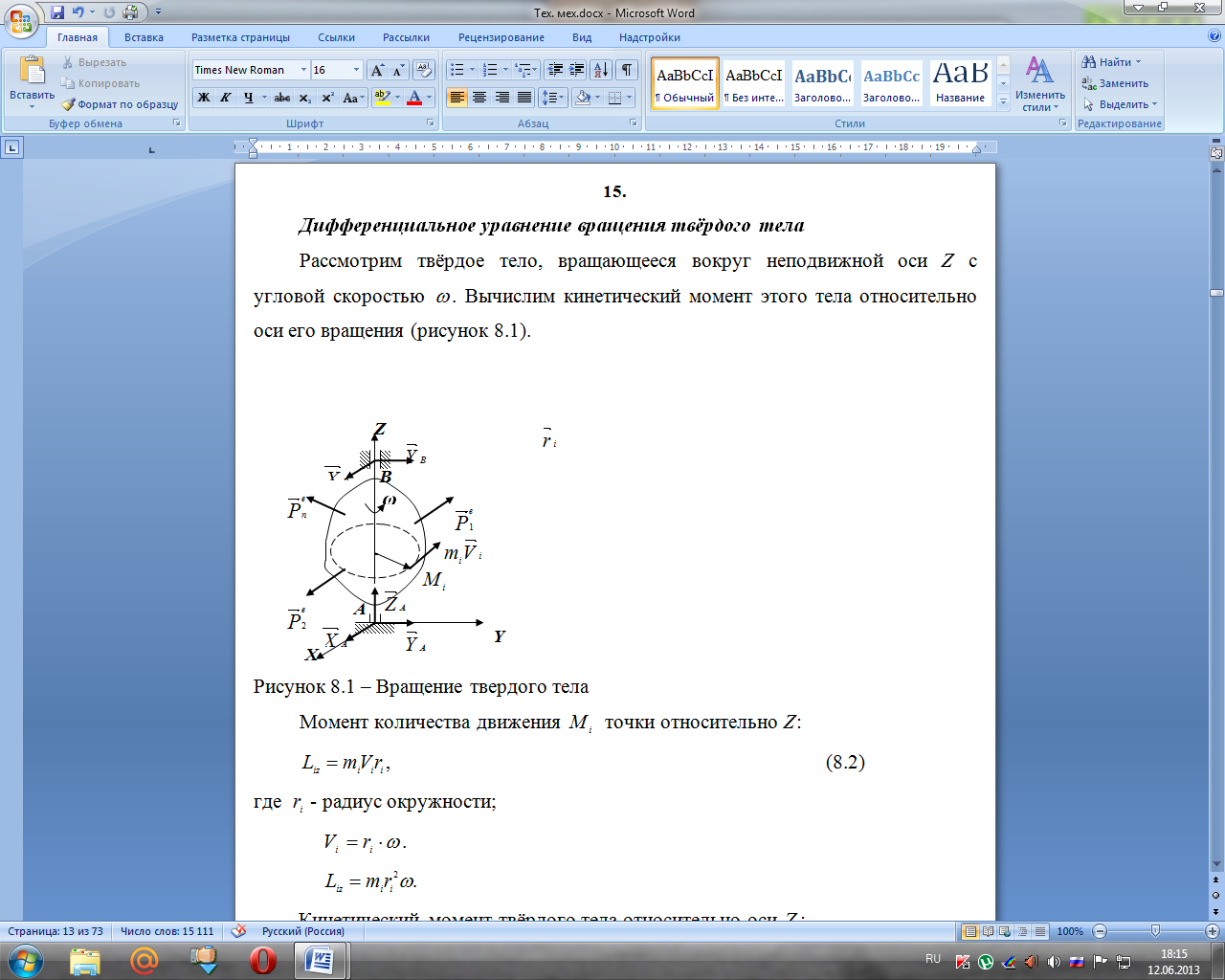
Момент количества движения точки относительно Z:

(8.2)

где - радиус окружности;

.

Кинетический момент твёрдого тела относительно оси :

Здесь - момент инерции твёрдого тела относительно оси .

. (8.3)

Кинетический момент вращающегося твёрдого тела относительно неподвижной оси его вращения равен произведению момента инерции тела относительно той же оси на угловую скорость тела.

Рассмотрим изменение кинетического момента тела относительно оси под действием приложенных внешних сил , , …,

Теорема об изменении кинетического момента механической системы:

. (8.4)

Теорема об изменении кинетического момента принимает

вид дифференциального уравнениятвёрдого тела:

. (8.5)

Момент инерции является характеристикой инертности тела при вращательном движении.

Если:

, то - тело вращается ускоренно;

, то , - тело вращается равномерно;

, то - тело вращается замедленно.

По дифференциальному уравнению вращения твёрдого тела можно решать следующие задачи:

• по заданному уравнению и моменту определить главный момент внешних сил;

• по заданным внешним силам и начальным условиям , и находят ;

• по и определяют момент инерции .

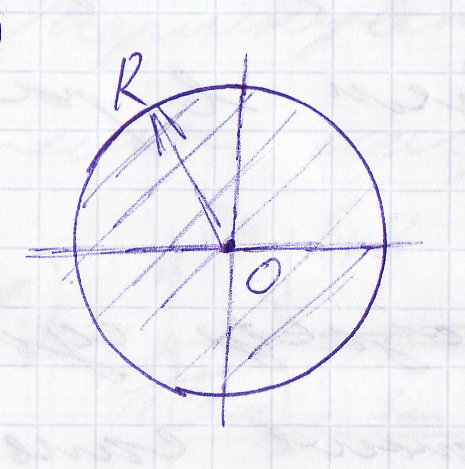
16

Сплошной диск

Полый цилиндр

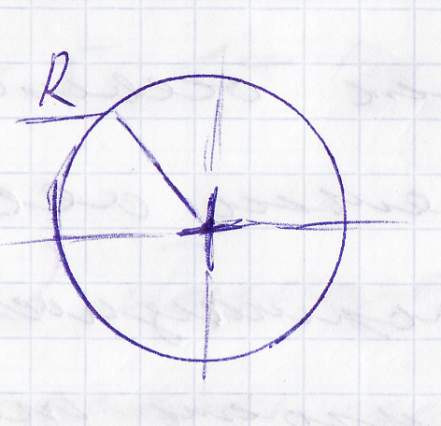
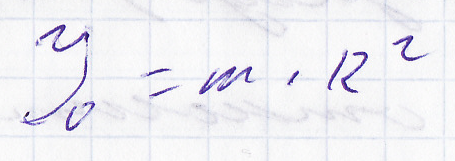
Однородный стержень

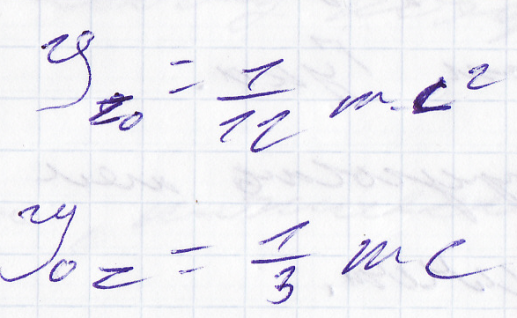
17.

Основные гипотезы о деформируемом твёрдом теле.

• Однородность, изотропность

• Свойства этих материалов должны быть одинаковы по всем свойствам и допущениям

• В силу малой деформации мы не используем её расчётах

• Принцип супер позиции (всё сложное есть сумма простых)

• Перпендикулярность осевых сечений относительно осевой при малых деформациях.

• Упругость тел при определённых моментах (закон Гука)

• Упругость тел до определённой величины.

18.

Деформации продольные и поперечные. Закон Гука

При действии внешней силы Р брус удлиняется в продольном направлении и его поперечные размеры сокращаются (рисунок 2.2).

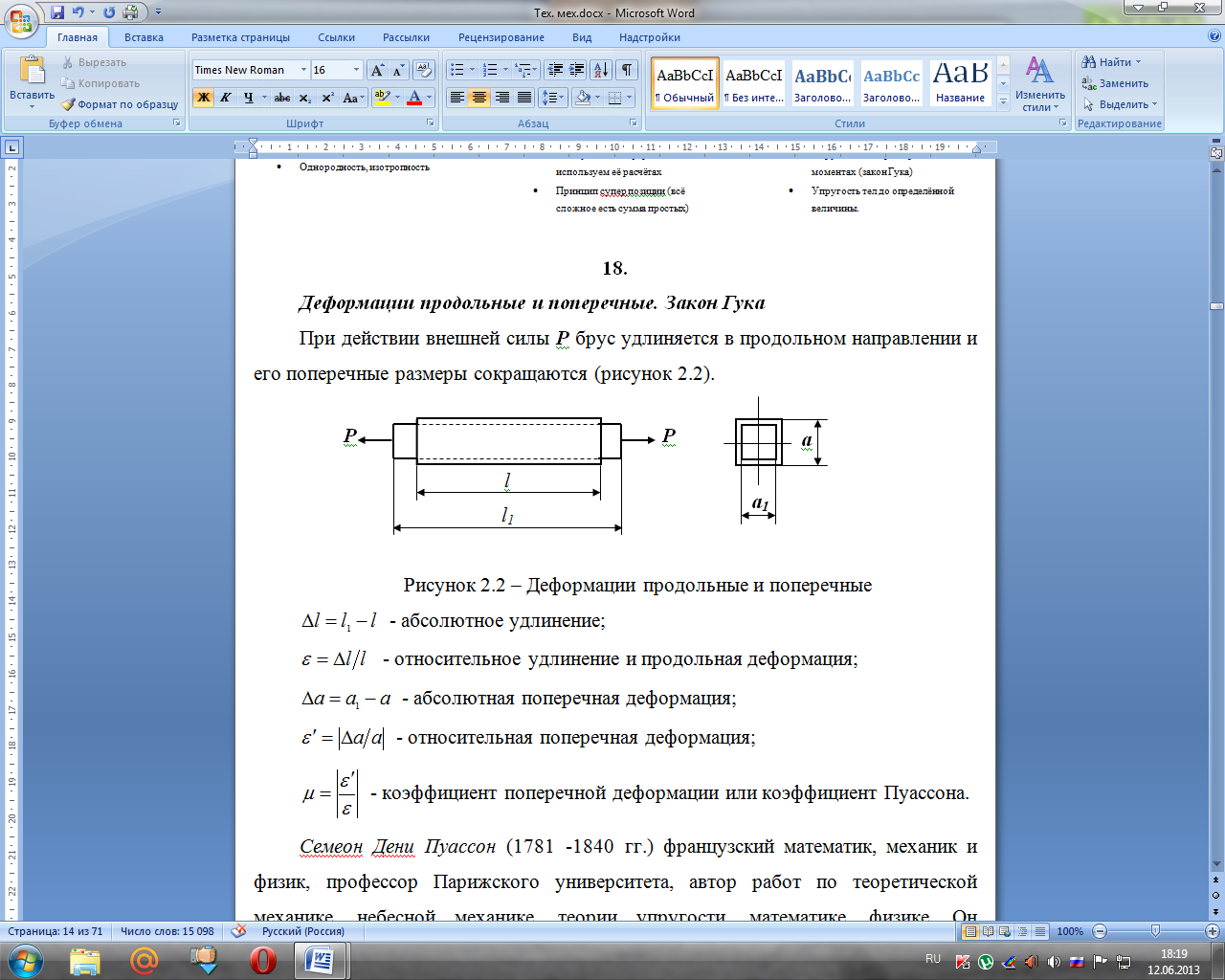
Рисунок 2.2 – Деформации продольные и поперечные

- абсолютное удлинение;

- относительное удлинение и продольная деформация;

- абсолютная поперечная деформация;

- относительная поперечная деформация;

- коэффициент поперечной деформации или коэффициент Пуассона.

Семеон Дени Пуассон (1781 -1840 гг.) французский математик, механик и физик, профессор Парижского университета, автор работ по теоретической механике, небесной механике, теории упругости, математике, физике. Он теоретически установил, что для всех материалов . Экспериментами это не подтвердилось.

Опытами установлено, что для различных материалов =0 … 0,5. Сталь =0,25; каучук =0,5; пробка =0.

Английский ученый Роберт Гук в 1678 г установил закон, который получил его имя.

Роберт Гук (1635 – 1703 гг.), английский естествоиспытатель, ученый, изобретатель, архитектор. Ему принадлежат работы по совершенствованию микроскопа, барометра, зеркального телескопа. Одно время, он занимался изучением поведения пружин, и его осенила догадка, что все тела, а не только пружины обладают свойством упругости.

Закон Гука «Напряжение пропорционально деформации».

где Е – модуль продольной упругости или модуль Юнга;

ε – относительное удлинение.

Томас Юнг (1773 – 1829 гг.) английский физик. Ему принадлежат важные работы по волновой теории света (по интерференции и дифракции), известен работами по медицине и языковедению, ввел в технические расчеты , величину постоянную для данного материала.

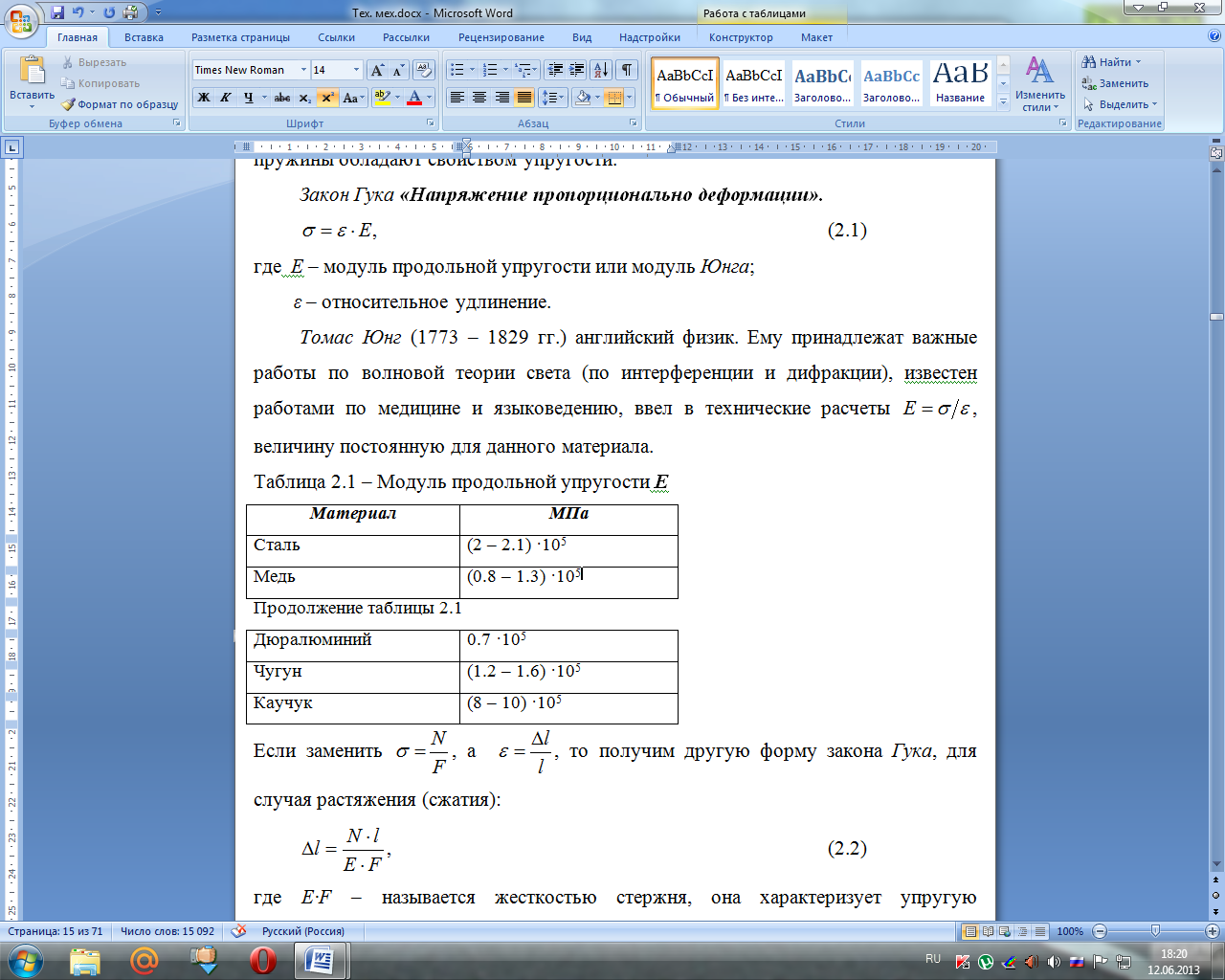
Таблица 2.1 – Модуль продольной упругости Е

Если заменить , а , то получим другую форму закона Гука, для случая растяжения (сжатия):

где E·F – называется жесткостью стержня, она характеризует упругую податливость стержня при его растяжении (сжатии).