
- •4.2 Возможные случаи приведения сил
- •5.2 Угол трения
- •3.5 Передаточные механизмы
- •4.4 Работа силы упругости
- •8.1 Дифференциальные уравнения поступательного движения
- •2.3 Растяжение под действием сил тяжести
- •2.4 Эпюры продольных сил, напряжений и перемещений
- •4.1 Расчетные зависимости. Три типа прочностных задач
- •16.2 Механизмы усталостного разрушения
- •16.3 Циклы изменения напряжений
- •16.5 Основные факторы, влияющие на прочность деталей
4.4 Работа силы упругости
Рассмотрим пружину
 (рисунок 4.4). Конец А
закреплён. При растяжении возникает
сила сопротивления со стороны пружины
(рисунок 4.4). Конец А
закреплён. При растяжении возникает
сила сопротивления со стороны пружины
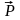 .
Её модуль пропорционален удлинению:
.
Её модуль пропорционален удлинению:
 ,
(4.14)
,
(4.14)
где С – коэффициент жёсткости пружины.
Проекция силы упругости на ось X:
 .
.
Элементарная работа:

где
 ;
;
;
;
 - проекции силы
на оси координат.
- проекции силы
на оси координат.
Элементарная работа силы упругости:
 .
.
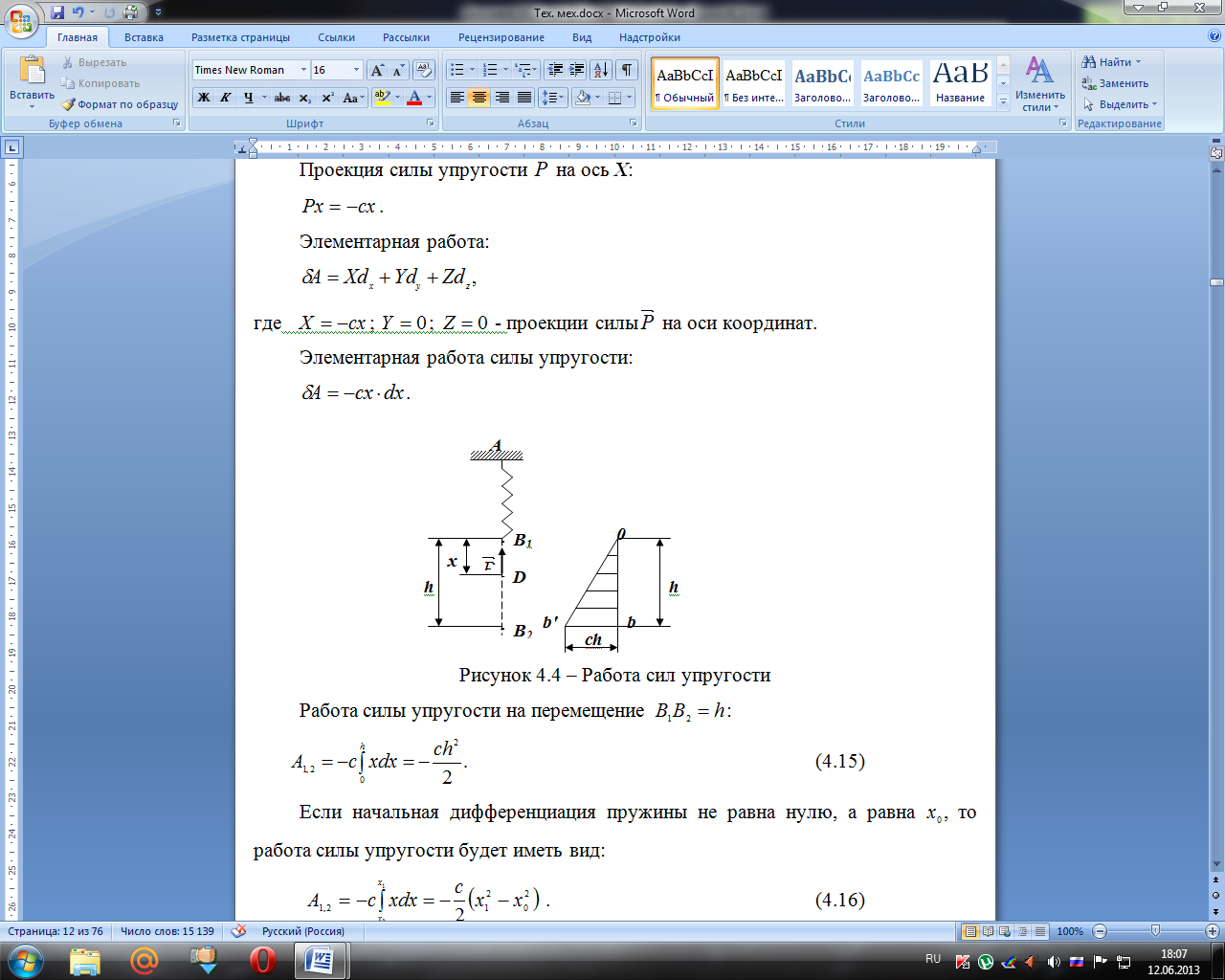
Рисунок 4.4 – Работа сил упругости
Работа силы
упругости на перемещение
 :
:
 (4.15)
(4.15)
Если начальная
дифференциация пружины не равна нулю,
а равна
 ,
то работа силы упругости будет иметь
вид:
,
то работа силы упругости будет иметь
вид:
 .
(4.16)
.
(4.16)
13.
Кинетическая энергия для механической системы
Установим зависимость между изменением кинетической энергии механической системы и работой сил приложенных к ней.
Силы,
действующие на точки
 ,
,
 ,
…,
,
…,
 ,
,
 ,
,
 ,
…,
,
…,
 -
внешние,
-
внешние,
 ,
,
 ,
…,
,
…,
 -
внутренние (рисунок 4.6).
-
внутренние (рисунок 4.6).
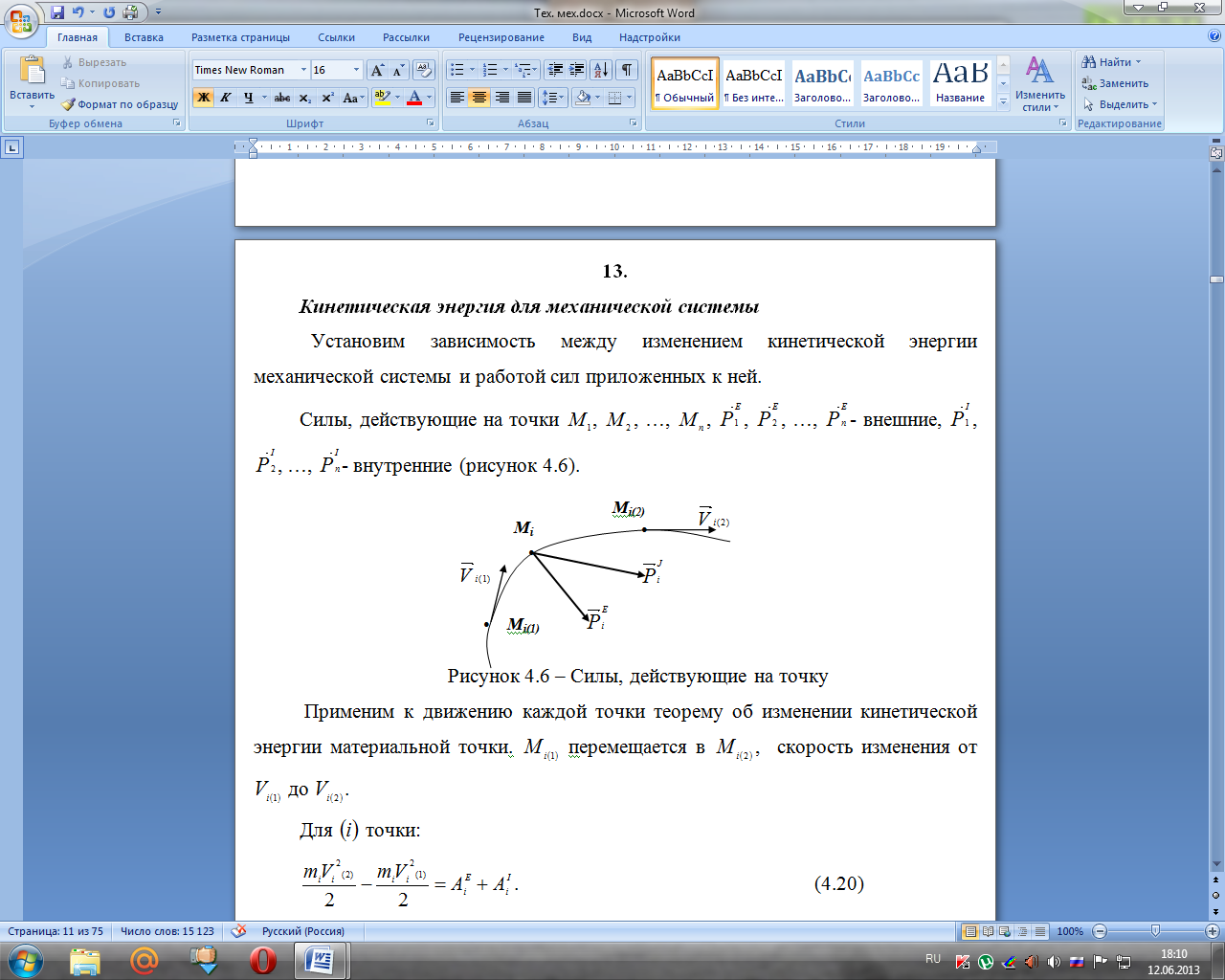
Применим
к движению каждой точки теорему об
изменении кинетической энергии
материальной точки.
 перемещается в
перемещается в
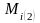 ,
скорость изменения от
,
скорость изменения от
 до
до
 .
.
Для
 точки:
точки:
 .
(4.20)
.
(4.20)
Для механической системы:
 ,
(4.21)
,
(4.21)
где
 - кинетическая энергия системы в первом
положении;
- кинетическая энергия системы в первом
положении;
 - кинетическая
энергии системы во втором
- кинетическая
энергии системы во втором
положении.
Тогда:
 .
(4.22)
.
(4.22)
Теорема об изменении кинетической энергии для механической системы.
Теорема: Изменение кинетической энергии механической системы на некотором перемещении равна сумме работ внешних и внутренних сил, действующих на материальные точки системы на этом перемещении.
Известно,
что работа внутренних сил по третьему
закону равна нулю.
 .
.
Тогда теорема об изменении кинетической энергии для твёрдого тела примет вид:
 .
(4.23)
.
(4.23)
Теорема: Изменение кинетической энергии твёрдого тела на некотором перемещении равна сумме работ внешних сил, действующих на тело на этом перемещении.
Кинетическая энергия механической системы равна сумме кинетических энергий тел, входящих в механическую систему (рисунок 4.7).
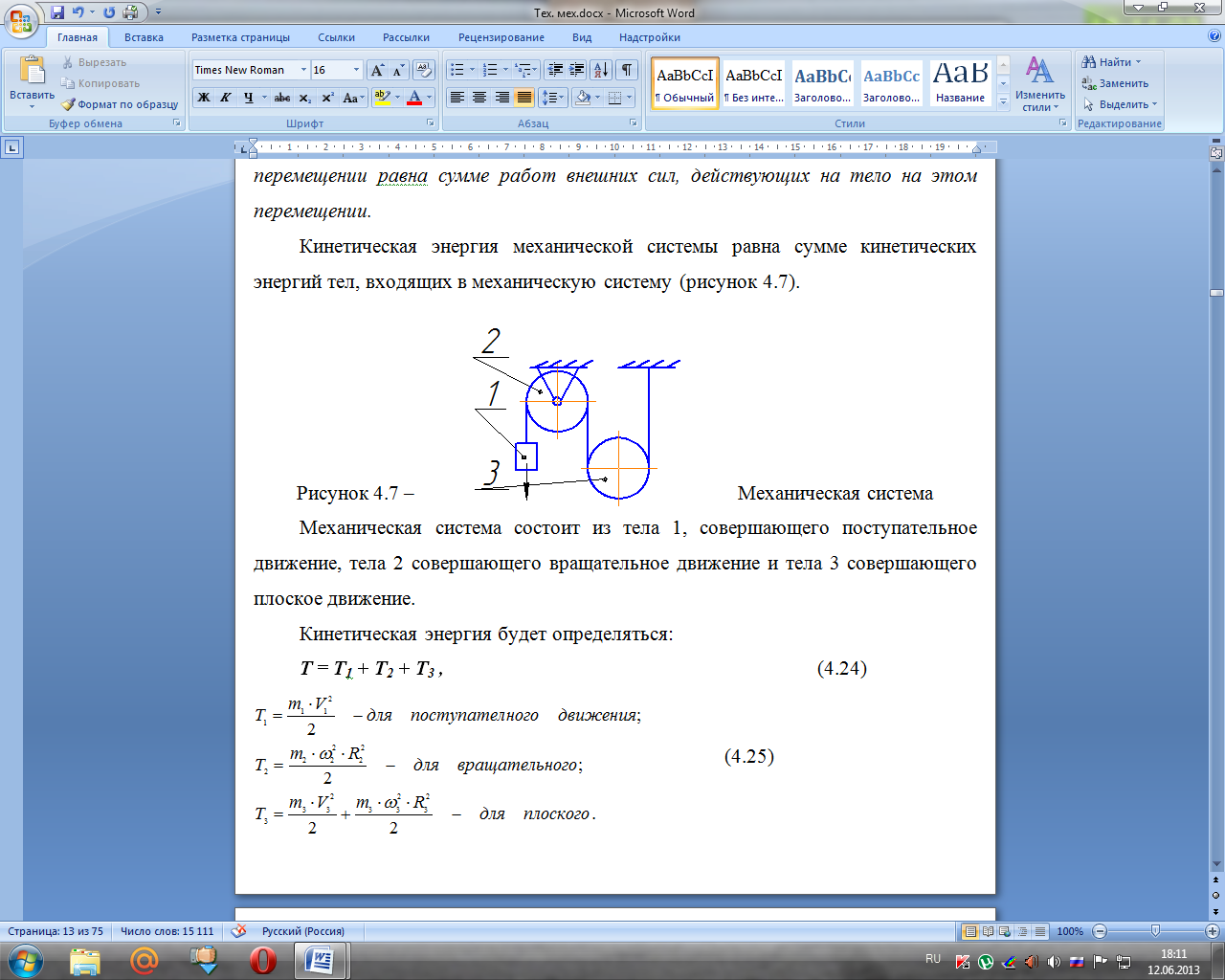
Рисунок 4.7 – Механическая система
Механическая система состоит из тела 1, совершающего поступательное движение, тела 2 совершающего вращательное движение и тела 3 совершающего плоское движение.
Кинетическая энергия будет определяться:
Т = Т1 + Т2 + Т3 , (4.24)
(4.25)

14.
Динамика твёрдого тела
