
- •4.2 Возможные случаи приведения сил
- •5.2 Угол трения
- •3.5 Передаточные механизмы
- •4.4 Работа силы упругости
- •8.1 Дифференциальные уравнения поступательного движения
- •2.3 Растяжение под действием сил тяжести
- •2.4 Эпюры продольных сил, напряжений и перемещений
- •4.1 Расчетные зависимости. Три типа прочностных задач
- •16.2 Механизмы усталостного разрушения
- •16.3 Циклы изменения напряжений
- •16.5 Основные факторы, влияющие на прочность деталей
1.
Сила – мера механического взаимодействия тел.
Силы подразделяются на внешние и внутренние. Внешние силы – все силы, действующие извне, включая силу веса. Внутренние силы – все то, что внутри системы. Внешние силы можно подразделить на активные (заданные) и реактивные (действующие со стороны связей).
Аксиомы статики
Аксиома 1 (инерции). Всякая точка, (тело) находится в состоянии покоя или равномерно прямолинейно движется, до тех пор, пока приложенные силы не выведут её из этого состояния.
Аксиома
2(равновесия
двух сил).
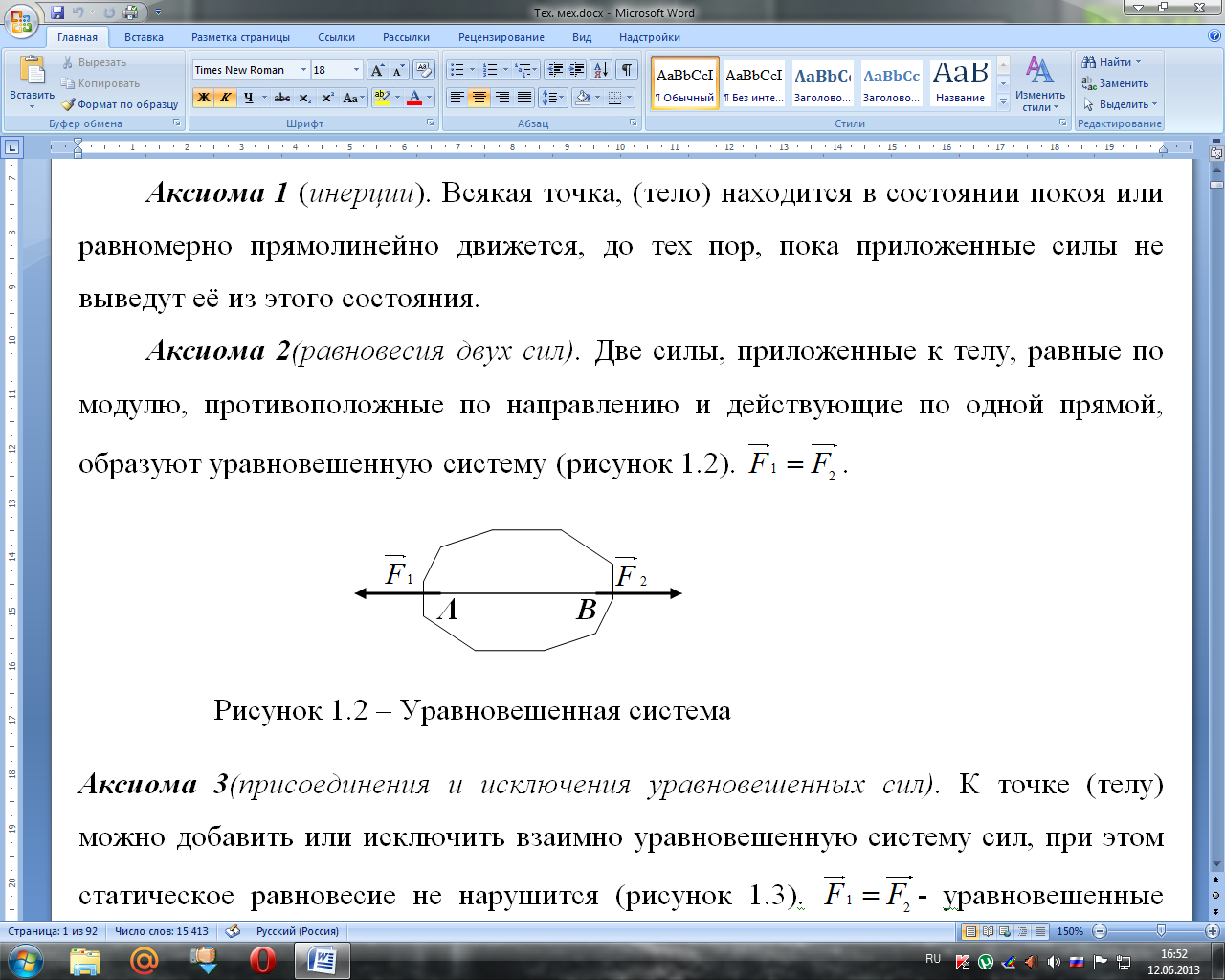
Две силы, приложенные к телу, равные по
модулю, противоположные по направлению
и действующие по одной прямой, образуют
уравновешенную систему (рисунок 1.2).
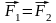 .
.
Аксиома 3(присоединения и исключения уравновешенных сил). К точке (телу) можно добавить или исключить взаимно уравновешенную систему сил, при этом статическое равновесие не нарушится (рисунок 1.3). - уравновешенные силы.

Следствие: Не нарушая равновесия, силу можно переносить по линии действия силы (рисунок 1.4).
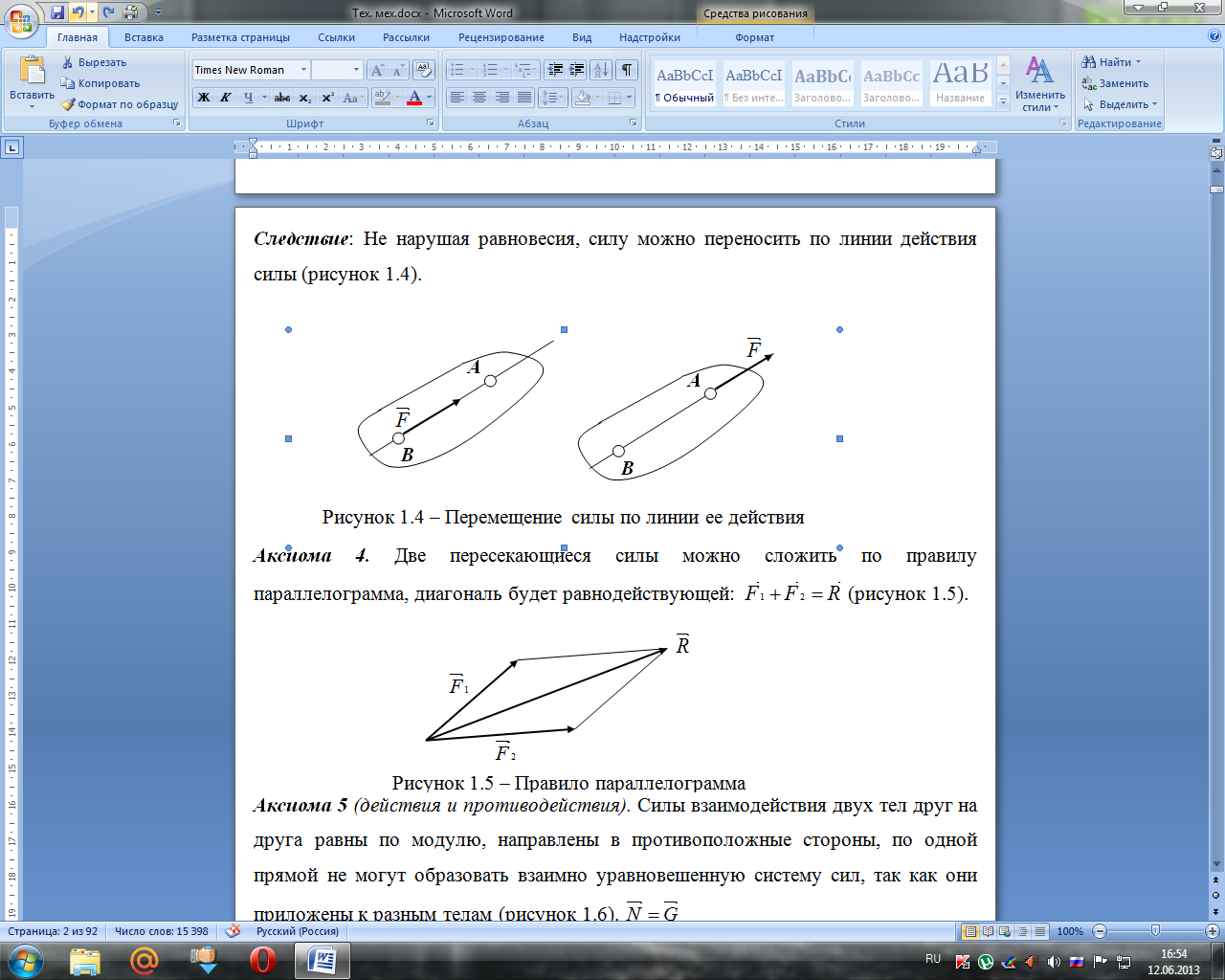
Аксиома 4.
Две пересекающиеся силы можно сложить
по правилу параллелограмма, диагональ
будет равнодействующей:
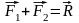 (рисунок 1.5).
(рисунок 1.5).
Аксиома 5
(действия
и противодействия).
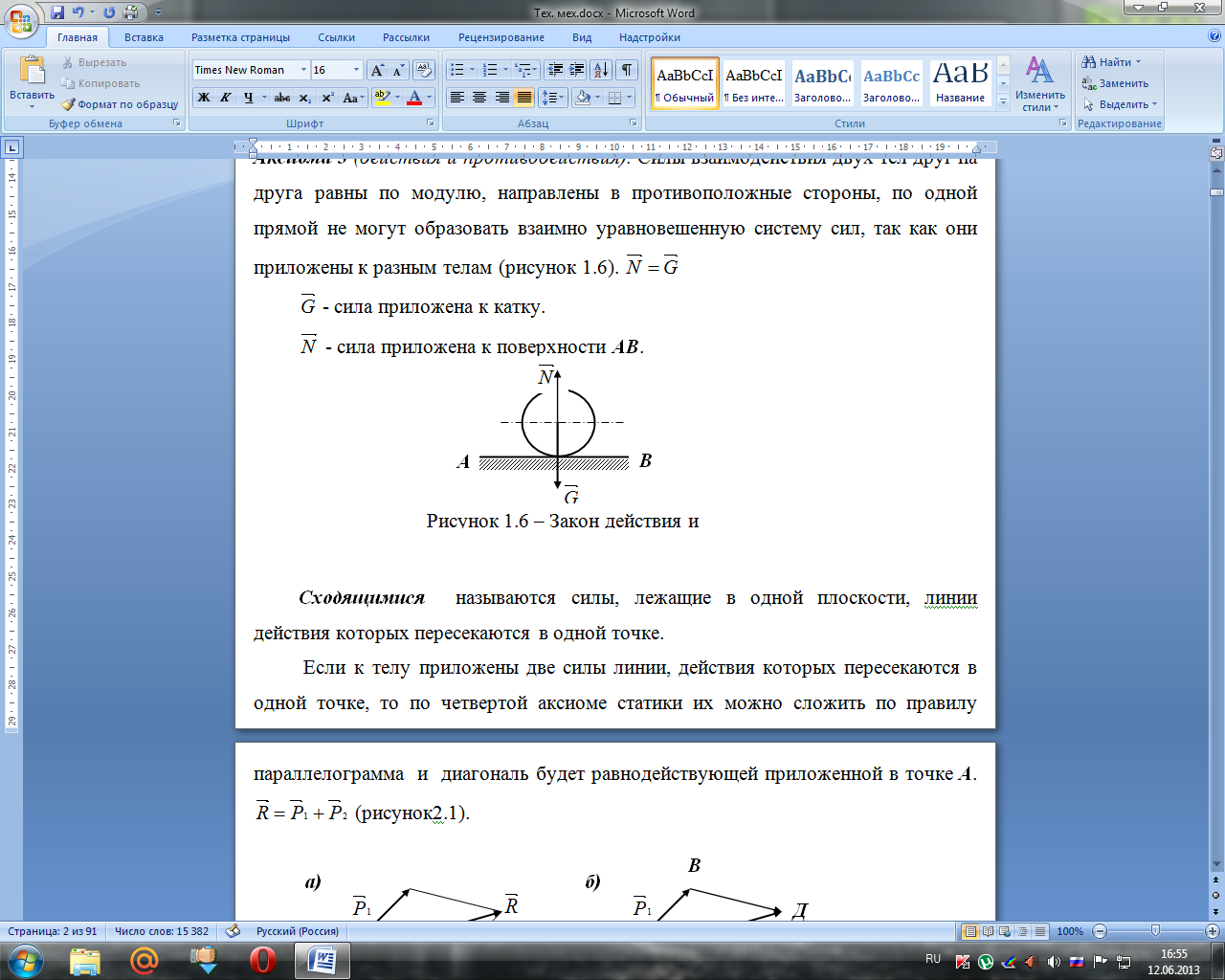
Силы взаимодействия двух тел друг на
друга равны по модулю, направлены в
противоположные стороны, по одной
прямой не могут образовать взаимно
уравновешенную систему сил, так как
они приложены к разным телам (рисунок
1.6).
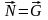
 - сила приложена к катку.
- сила приложена к катку.
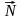 - сила приложена
к поверхности АВ.
- сила приложена
к поверхности АВ.
Сходящимися называются силы, лежащие в одной плоскости, линии действия которых пересекаются в одной точке.
Если к телу
приложены две силы линии, действия
которых пересекаются в одной точке, то
по четвертой аксиоме статики их можно
сложить по правилу параллелограмма и
диагональ будет равнодействующей
приложенной в точке А.
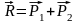 (рисунок2.1).
(рисунок2.1).

Построение параллелограмма сил можно заменить постарением треугольника сил АВД.
Направление
равнодействующей силы
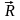 по контуру силового треугольника,
противоположно направлению обхода
контура треугольника, определяемому
слагаемыми силами.
по контуру силового треугольника,
противоположно направлению обхода
контура треугольника, определяемому
слагаемыми силами.
При помощи
параллелограмма или треугольника сил
можно решить и обратную задачу –
разложить силу
на две составляющие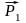 и
и
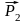 приложенные в той же точке и направленные
по заданным линиям действия (рисунок
2.2).
приложенные в той же точке и направленные
по заданным линиям действия (рисунок
2.2).
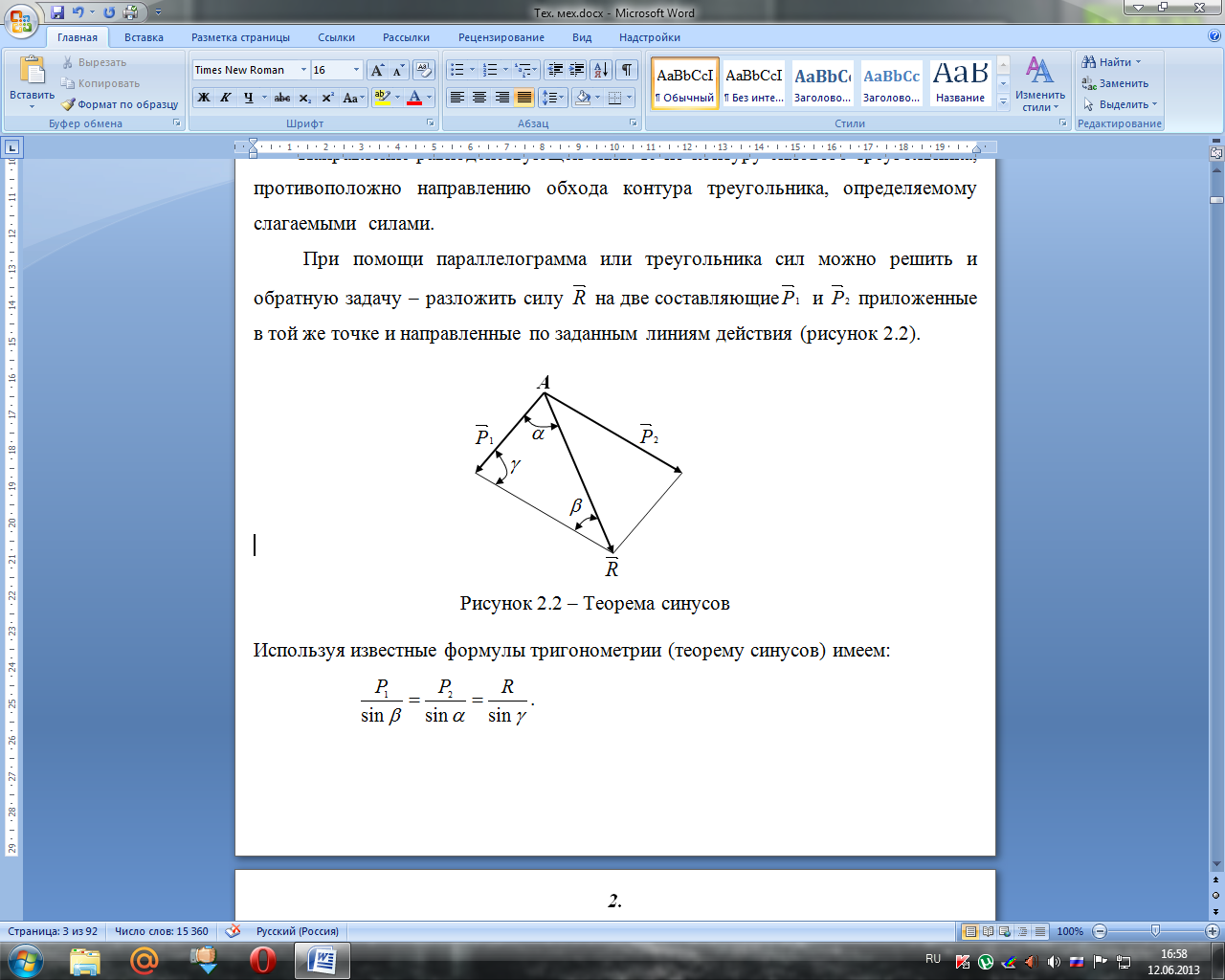
Используя известные формулы тригонометрии (теорему синусов) имеем:

 .
.
2.
Аналитические условия равновесия
Равнодействующая
сходящихся сил
 равна геометрической сумме этих сил
равна геометрической сумме этих сил 
Проекция равнодействующей на каждую из координатных осей равна алгебраической сумме проекции всех составляющих:
X = X1 + X2 + Х3 +…+Xn;
Y = Y1 + Y2 + Y3 +…+Yn;
Z = Z1 + Z2 + Z3+…+Zn,
где
X,Y,Z
– проекция равнодействующей на
координатные оси;X1
= P1
cos(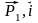 ),
X2
= P2
cos(
),
X2
= P2
cos( ),
… , Xn
= Pn
cos(
),
… , Xn
= Pn
cos(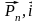 );
);
Y1
= P1
cos( ),
Y2
= P2
cos(
),
Y2
= P2
cos(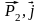 ),
… , Yn
= Pn cos(
),
… , Yn
= Pn cos( );
(2.9)
);
(2.9)
Z1
= P1
cos(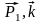 );
Z2
= P2
cos(
);
Z2
= P2
cos(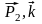 ),
…, Zn
= Pn cos(
),
…, Zn
= Pn cos( ).
).
Формулам (2.8) можно придать вид:
X=∑Xi; Y=∑Yi; Z=∑Zi. (2.10)
Найдем
модуль равнодействующей:
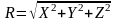 .
(2.11)
.
(2.11)
В случае, если силы взаимно уравновешиваются, их равнодействующая R = 0. Так как = 0 то X = 0; Y=0; Z=0.
Таким образом, для сходящихся сил в пространстве имеем три уравнения равновесия:
X1 +X2 +… +Xn = 0 или ∑Xi = 0;
Y1 +Y2 +… +Yn = 0 или ∑Yi = 0; (2.12)
Z1 + Z 2+…+ Zn = 0 или ∑Zi = 0.
Выражение (2.12) есть аналитические условия статического равновесия сходящейся системы сил.
3.
Плоская система произвольно расположенных сил
Приведение сил к заданному центру
Пусть дана сила
 ,
приложенная к точке А
твердого тела, и ее требуется перенести
в точку О
(рисунок 4.1).
,
приложенная к точке А
твердого тела, и ее требуется перенести
в точку О
(рисунок 4.1).
Приложим к телу в
точке О
уравновешенную систему сил
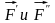 ,
параллельных
и равных ей по модулю (
,
параллельных
и равных ей по модулю (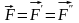 ).
).
Кроме силы
 ,
приложенной к точке О,
образовалась пара сил (
,
приложенной к точке О,
образовалась пара сил (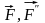 )
с моментом
)
с моментом
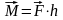 ,
но и момент данной силы
относительно точки О
,
но и момент данной силы
относительно точки О
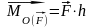 ,
т.е.
,
т.е. .
.
Таким образом ,всякую силу приложенную к телу в точке А, можно переносить параллельно линии действия в любую точку О, добавив момент равный моменту данной силы относительно точки приведения (метод Пуансо).
Применяя метод
Пуансо приведем систему произвольно
расположенных сил
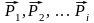 приложенных
к точкам А1,
А2,
… , Аi
к заданному центру О
(рисунок
4.2).
приложенных
к точкам А1,
А2,
… , Аi
к заданному центру О
(рисунок
4.2).
В результате приведение системы произвольно расположенных сил к заданному центру образовалась система сходящихся сил с моментами заданных сил.
При помощи силового многоугольника находим равнодействующую равную геометрической сумме заданных сил приложенную в центре приведения (рисунок 4.3)
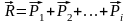 .
(4.1)
.
(4.1)
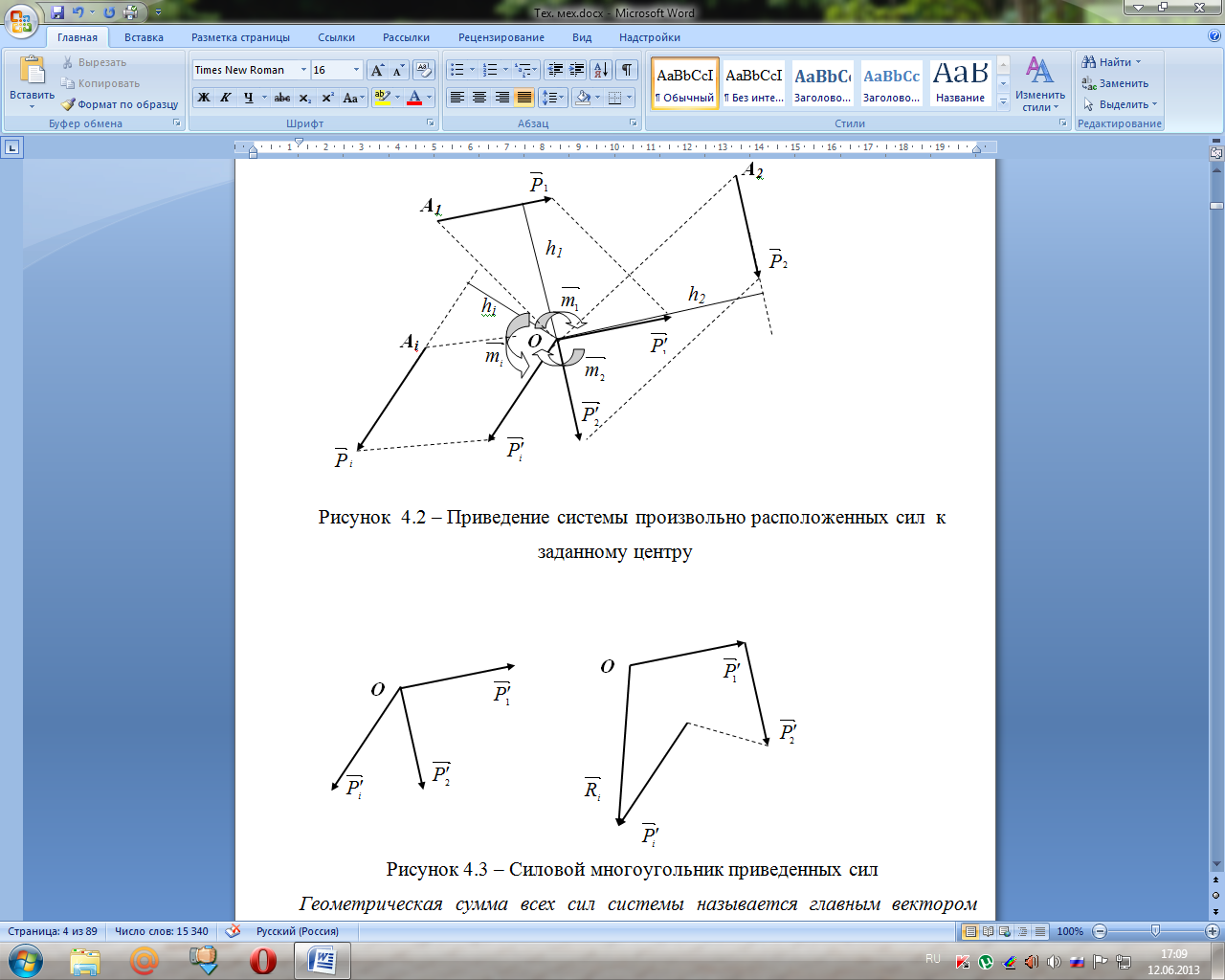
Геометрическая
сумма всех сил системы называется
главным вектором системы сил,
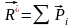 .
.
Вектора
моментов:
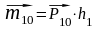 ;
;
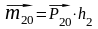 ;
;

направлены перпендикулярно плоскости, в которой находятся и силы, и центр. Определим сумму, сложив геометрически моменты:
 ,
(4.3)
,
(4.3)
где
 - главный момент.
- главный момент.
Сложение векторов моментов (рисунок 4.4)

П лоская произвольная система сил приводится к главному вектору и главному моменту.
4.2 Возможные случаи приведения сил
I.
 - статическое равновесие.
- статическое равновесие.
II.
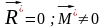 -
система приводится к паре сил, момент
пары сил равен главному моменту
относительно центра привидения.
-
система приводится к паре сил, момент
пары сил равен главному моменту
относительно центра привидения.
III.
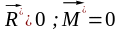 - силы приводятся к равнодействующей,
линия действия которой проходит через
центр привидения.
- силы приводятся к равнодействующей,
линия действия которой проходит через
центр привидения.
4.
Трение скольжения
Если
к твердому телу, покоящемуся на
шероховатой горизонтальной плоскости,
приложить горизонтальную силу
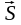 ,
то действие этой силы вызывает появление
силы сцепления
,
то действие этой силы вызывает появление
силы сцепления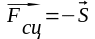 ,
представляющей собой силу противодействия
плоскости смещению тела. Благодаря
сцеплению тело остаётся в покое. При
изменение модуля силы S
от нуля до некоторого значения Smax
(рисунок
5.1).
,
представляющей собой силу противодействия
плоскости смещению тела. Благодаря
сцеплению тело остаётся в покое. При
изменение модуля силы S
от нуля до некоторого значения Smax
(рисунок
5.1).
Fсц = fсц * N, (5.1)
где fсц – коэффициент сцепления;
N – реакция нормального давления;
R – реакция шероховатой поверхности.
Направление силы сцепления противоположно направлению движения.
Модуль силы трения скольжения пропорционален нормальному давлению:
Fтр = f * N, (5.2)
где f –коэффициент трения скольжения.

Коэффициент трения скольжения является отвлеченной величиной и зависит от материала и физического состояния трущихся поверхностей, а также от скорости движения тела и удельного давления. В элементарных расчетах зависимость коэффициента трения скольжения от скорости и удельного давления не учитываются.
Экспериментально установлено (рисунок 5.2), что:
f < fсц (5.3)

Рисунок 5.2 – Виды трений скольжения
5.2 Угол трения
Реакция
,
шероховатой поверхности, имеет две
составляющие:
–
нормальную реакцию и
 -
силу сцепления (или силу трения при
движении), рисунок 5.3.
-
силу сцепления (или силу трения при
движении), рисунок 5.3.

φсц – угол между реакцией шероховатой поверхности и нормальной реакции – угол сцепления.
Тангенс угла сцепления равен коэффициенту сцепления:
tg φсц = Fсц /N = fсц, (5.4)
где φсц = arctg fсц.
Угол, тангенс которого равен коэффициенту трения скольжения, называется углом трения.
Конус трения:
Рассмотрим равновесие невесомого тела на горизонтальной шероховатой плоскости под действием наклонной силы F1, стремящейся его сдвинуть.
Тело
будет сдвинуто только тогда, когда
![]() >
Fmax =
>
Fmax =![]() Предельному
случаю равновесия соответствует такой
угол наклона a, при котором выполняется
равенство
=
,
или tgα = f. Если tgα<=f, то как бы не
возрастала сила F1, тело сдвинуть с места
невозможно. Возрастающей сдвигающей
силе
будет противостоять пропорционально
ей увеличивающаяся сила трения
Поворачивая вокруг вертикали вектор
силы F1 и сохраняя при этом предельное
равновесие, опишем конус, называемый
конусом трения. Если свойства
соприкасающихся поверхностей во всех
направлениях одинаковы, то угол а будет
постоянным, а конус трения круговым.
Конус трения обладает тем замечательным
свойством, что если действующая на тело
сила находится внутри него, то тело
всегда будет находиться в равновесии.
Этим объясняются известные явления
заклинивания, или самоторможения тел.
Предельному
случаю равновесия соответствует такой
угол наклона a, при котором выполняется
равенство
=
,
или tgα = f. Если tgα<=f, то как бы не
возрастала сила F1, тело сдвинуть с места
невозможно. Возрастающей сдвигающей
силе
будет противостоять пропорционально
ей увеличивающаяся сила трения
Поворачивая вокруг вертикали вектор
силы F1 и сохраняя при этом предельное
равновесие, опишем конус, называемый
конусом трения. Если свойства
соприкасающихся поверхностей во всех
направлениях одинаковы, то угол а будет
постоянным, а конус трения круговым.
Конус трения обладает тем замечательным
свойством, что если действующая на тело
сила находится внутри него, то тело
всегда будет находиться в равновесии.
Этим объясняются известные явления
заклинивания, или самоторможения тел.
5.
Трение качения
Трением качения называется сопротивление, возникающее при качение одного тела по поверхности другого.
Рассмотрим
каток радиуса R
и весом
(рисунок 5.4) на горизонтальной, шероховатой
поверхности. Приложим к точке
О силу .
В точке касания возникает сила трения,
направленная в противоположную сторону
движения.
.
В точке касания возникает сила трения,
направленная в противоположную сторону
движения.
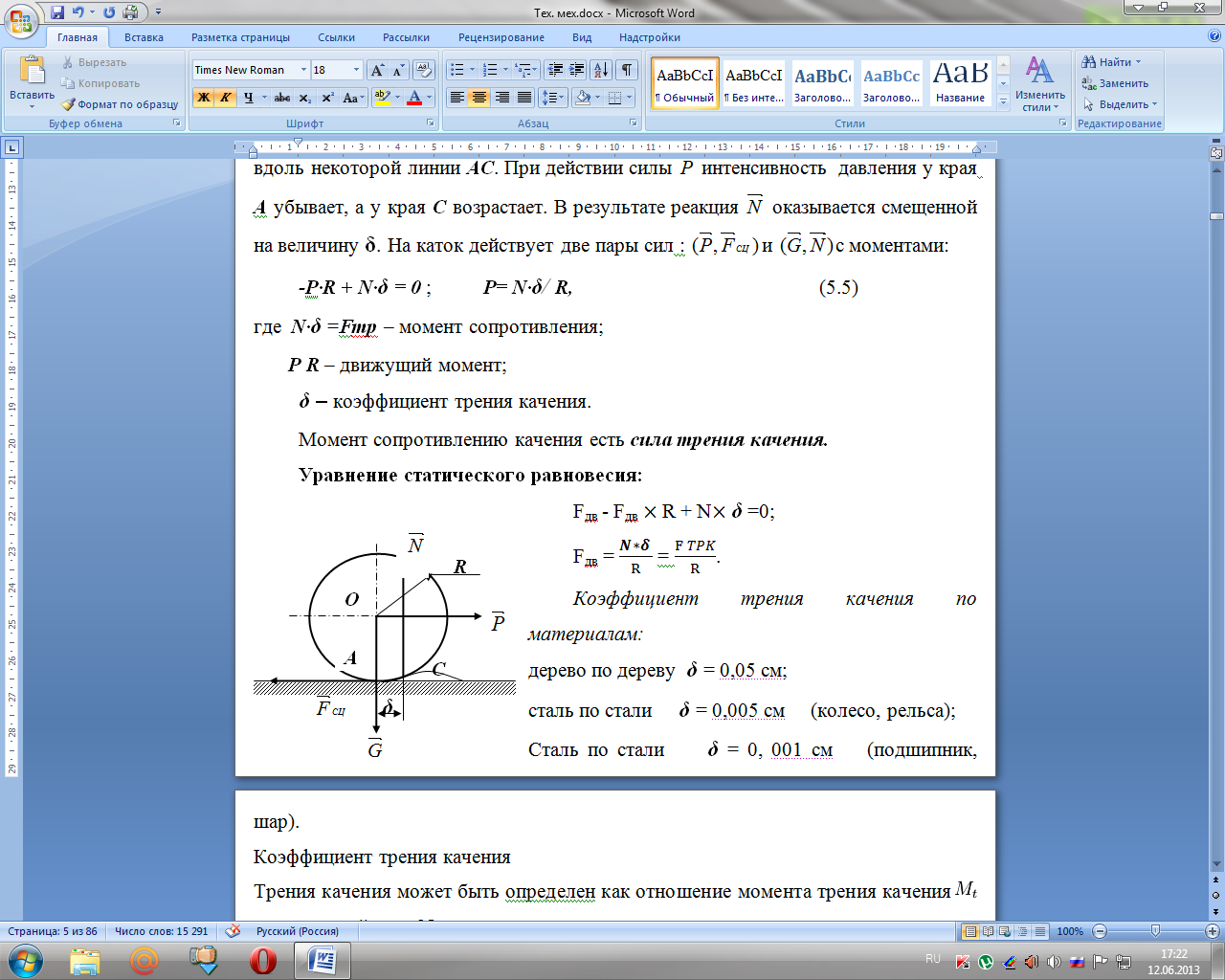
Рисунок 5.4 – Трение качения
В
следствии деформации тел, касание катка
с поверхностью происходит вдоль
некоторой линии АС.
При действии силы
интенсивность давления у края А
убывает, а у края С
возрастает. В результате реакция
оказывается смещенной на величину δ.
На каток действует две пары сил :
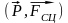 и
и
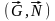 с
моментами:
с
моментами:
-Р·R + N·δ = 0 ; Р= N·δ/ R, (5.5)
где N·δ =Fтр – момент сопротивления;
P R – движущий момент;
δ – коэффициент трения качения.
Момент сопротивлению качения есть сила трения качения.
Уравнение статического равновесия:
Fдв - Fдв
 R + N
δ =0;
R + N
δ =0;
Fдв =
 =
=
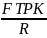 .
.
Коэффициент трения качения по материалам:
дерево по дереву δ = 0,05 см;
сталь по стали δ = 0,005 см (колесо, рельса);
Сталь по стали δ = 0, 001 см (подшипник, шар).
Коэффициент трения качения
Трения
качения может быть определен как
отношение момента трения качения![]() к прижимной силе N:
к прижимной силе N:
![]()
Коэффициент трения качения имеет следующие физические интерпретации:
Если тело находится в покое и внешняя сила отсутствует, то реакция опоры лежит на той же линии, что и прижимающая сила. Когда тело катится, то из условия равновесия следует, что нормальная составляющая реакции опоры параллельна и противонаправлена прижимающей силе, но не лежит с ней на одной линии. Коэффициент трения качения равен расстоянию между прямыми, вдоль которых действуют прижимающая сила и нормальная составляющая реакции опоры.
Движение катящегося тела без проскальзывания можно рассматривать как поворот вокруг мгновенной оси вращения (на рис. 4 — точка приложения вектора ), которая для абсолютно твёрдых тел совпадает с основанием перпендикуляра, опущенного из центра круга на опору. Для случая реальных (деформирующихся под нагрузкой) материалов мгновенный центр вращения смещён в направлении качения тела, а величина смещения равна значению коэффициента трения качения.
6.
Момент силы относительно точки и относительно оси
Момент
силы
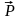 относительно
точки О
(рисунок 3.7) изображается вектором
относительно
точки О
(рисунок 3.7) изображается вектором
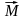 ,
приложенным в этой точке и направленным
перпендикулярно к плоскости,
содержащей силу и точку, в такую
сторону чтобы смотря на встречу этому
вектору, видеть силу
вращающую плоскость в обратную сторону
вращения часовой стрелки.
,
приложенным в этой точке и направленным
перпендикулярно к плоскости,
содержащей силу и точку, в такую
сторону чтобы смотря на встречу этому
вектору, видеть силу
вращающую плоскость в обратную сторону
вращения часовой стрелки.
Момент силы относительно центра можно записать в виде скалярного произведения:

 .
(3.5)
.
(3.5)
Или
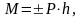 (3.6)
(3.6)
где h – плечо (наикротчайшее расстояние от центра до линии действия силы).
Из треугольника АОК, h = r sinα. Тогда M = P r sinα.
Моментом силы называется произведение модуля силы на плечо.
Момент силы относительно точки равен нулю, если h =0.
Моментом силы относительно оси называется произведение проекции силы, на плоскость перпендикулярную оси, на кратчайшее расстояние от точки пересечения оси с плоскостью до линии действия проекции (рисунок 3.8).
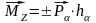 .
.
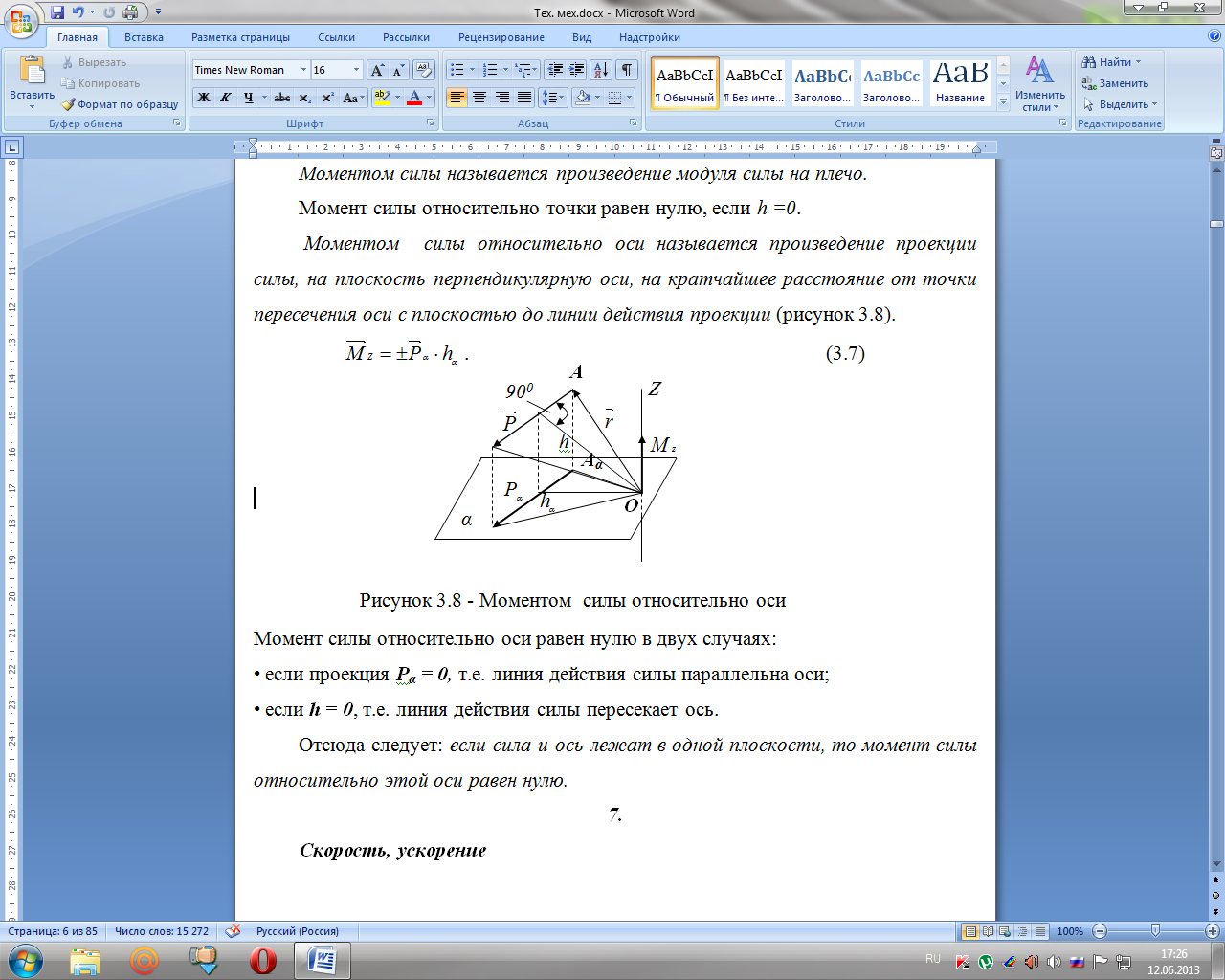
Момент силы относительно оси равен нулю в двух случаях:
• если проекция Рα = 0, т.е. линия действия силы параллельна оси;
• если h = 0, т.е. линия действия силы пересекает ось.
Отсюда следует: если сила и ось лежат в одной плоскости, то момент силы относительно этой оси равен нулю.
7.
Скорость, ускорение
Движущаяся точка при движении в пространстве описывает некоторую линию, которая называется траекторией точки. По виду траектории делятся на прямолинейные и криволинейные.
Изучение движения точки заключается в определении основных характеристик этого движения: положение, скорость, ускорение.
Существует три способа задания движения точки: векторный, координатный, естественный.
Векторный способ
Положение
точки в пространстве определим
радиус-вектором
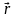 (рисунок 1.1), проведенного из неподвижного
центра О,
в данную точку.
(рисунок 1.1), проведенного из неподвижного
центра О,
в данную точку.
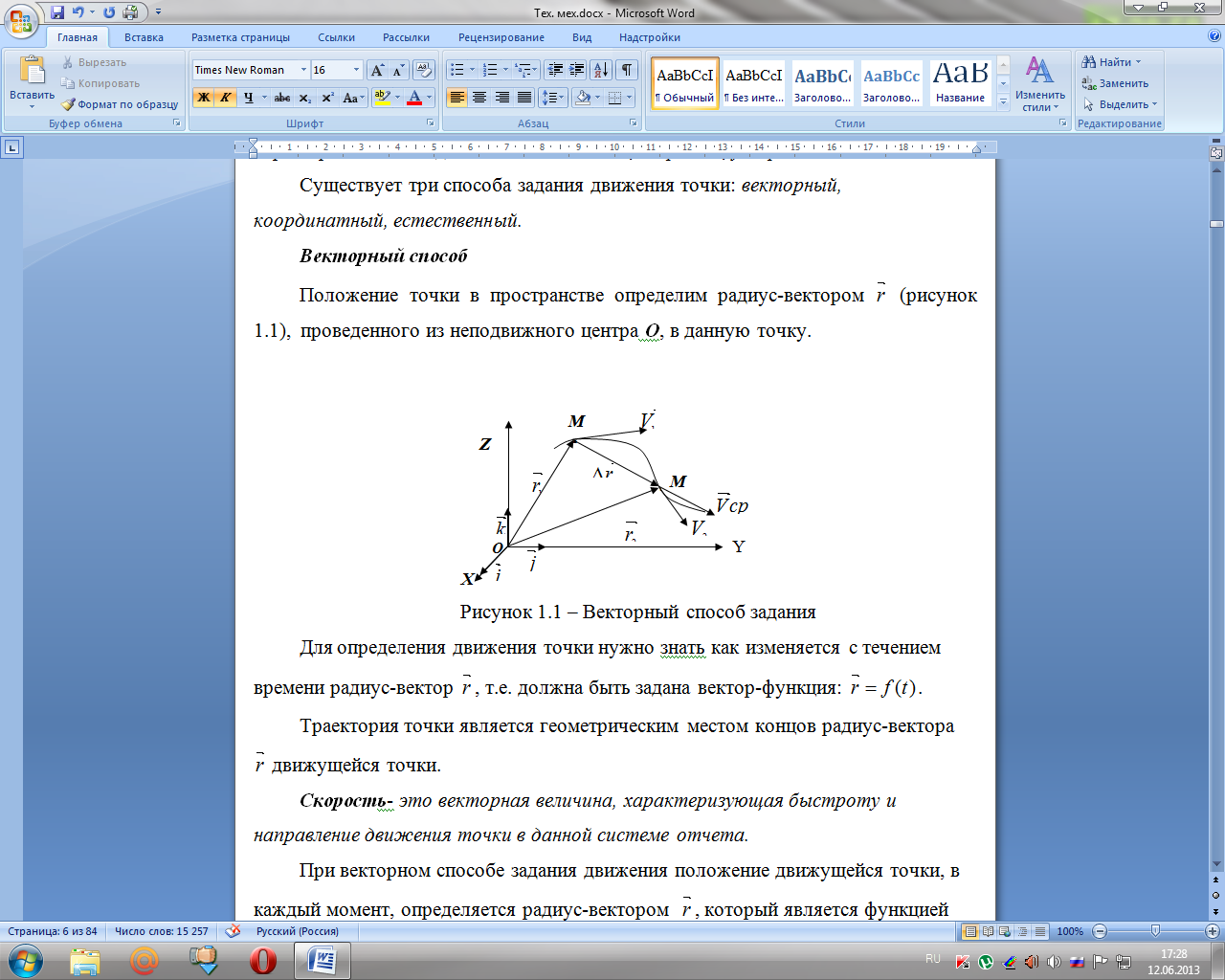
Рисунок 1.1 – Векторный способ задания
Для определения
движения точки нужно знать как изменяется
с течением времени радиус-вектор
,
т.е. должна быть задана вектор-функция:
 .
.
Траектория точки является геометрическим местом концов радиус-вектора движущейся точки.
Скорость- это векторная величина, характеризующая быстроту и направление движения точки в данной системе отчета.
При векторном способе задания движения положение движущейся точки, в каждый момент, определяется радиус-вектором , который является функцией времени .
В
момент времени t
точка
занимает положение М1
и определяется радиус-вектором
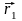 ,
а в момент времени t1
= t
+∆t
положение
М2
, определяется радиус-вектором
,
а в момент времени t1
= t
+∆t
положение
М2
, определяется радиус-вектором
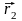 .
.
Из
треугольника ОМ1М2
(рисунок 1.1)
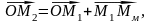 т.е.
т.е.
 (1.1)
(1.1)
Отношение
вектора перемещения
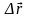 к промежутку времени
к промежутку времени
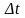 ,
в течении которого произошло это
перемещение, представляет собой вектор
средней скорости
,
в течении которого произошло это
перемещение, представляет собой вектор
средней скорости
 воображаемого движения точки М
по хорде:
воображаемого движения точки М
по хорде:
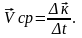 (1.2)
(1.2)
Направление вектора совпадает с направлением . При рассмотрении предела отношения к , при → 0 получим скорость точки.
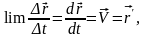 (1.3)
(1.3)
при → 0.
Вектор скорости точки в данный момент равен производной от радиус-вектора и направлен по касательной к траектории в сторону движения точки. Ускорение При неравномерном криволинейном движении точки изменяется модуль и направление скорости. Ускорение характеризует быстроту изменения модуля и направления скорости (рисунок 1.2).
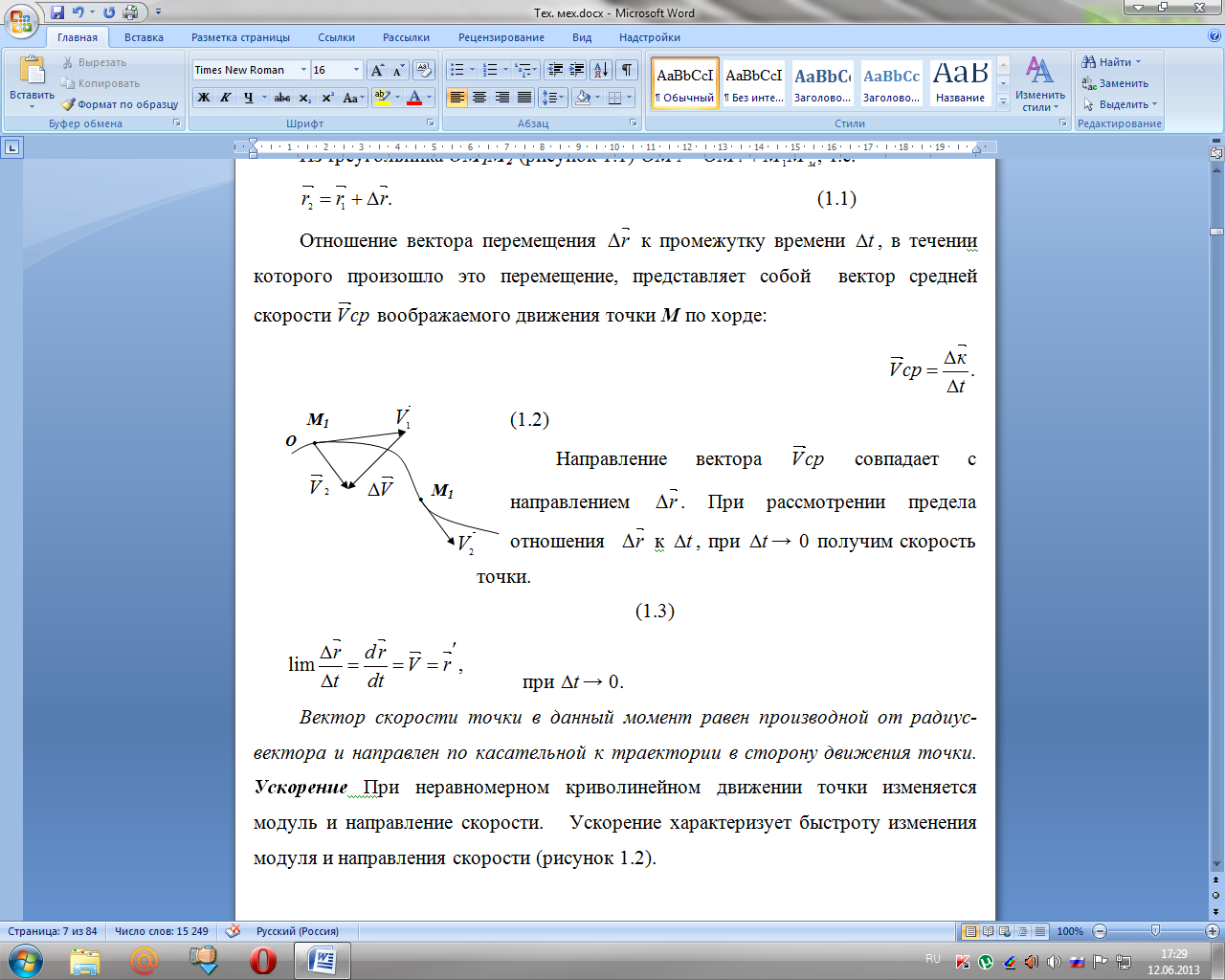
Рисунок 1.2 – Приращение скорости
В момент времени t точка находилась в М1, в момент времени
t1
= t
+∆t
она занимает положение М2.Соответственно
в М1
скорость равна
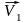 ,
а в М2
скорость равна
,
а в М2
скорость равна
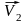 .
Найдем
.
Найдем
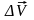 ,
смотри рисунок 1.2.
,
смотри рисунок 1.2.
 (1.4)
(1.4)
при → 0.
Ускорение – это производная скорости или вторая производная от радиус-вектора.
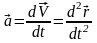 .
(1.5)
.
(1.5)
Координатный способ задания движения точки. Скорость, ускорение
Положение точки М в системе отчета OXYZ определяется тремя декартовыми координатами x, y, z. При движении точки координаты изменяются с течением времени. Следовательно, координаты: x, y, z движущейся точки М являются функциями времени (рисунок 1.3).
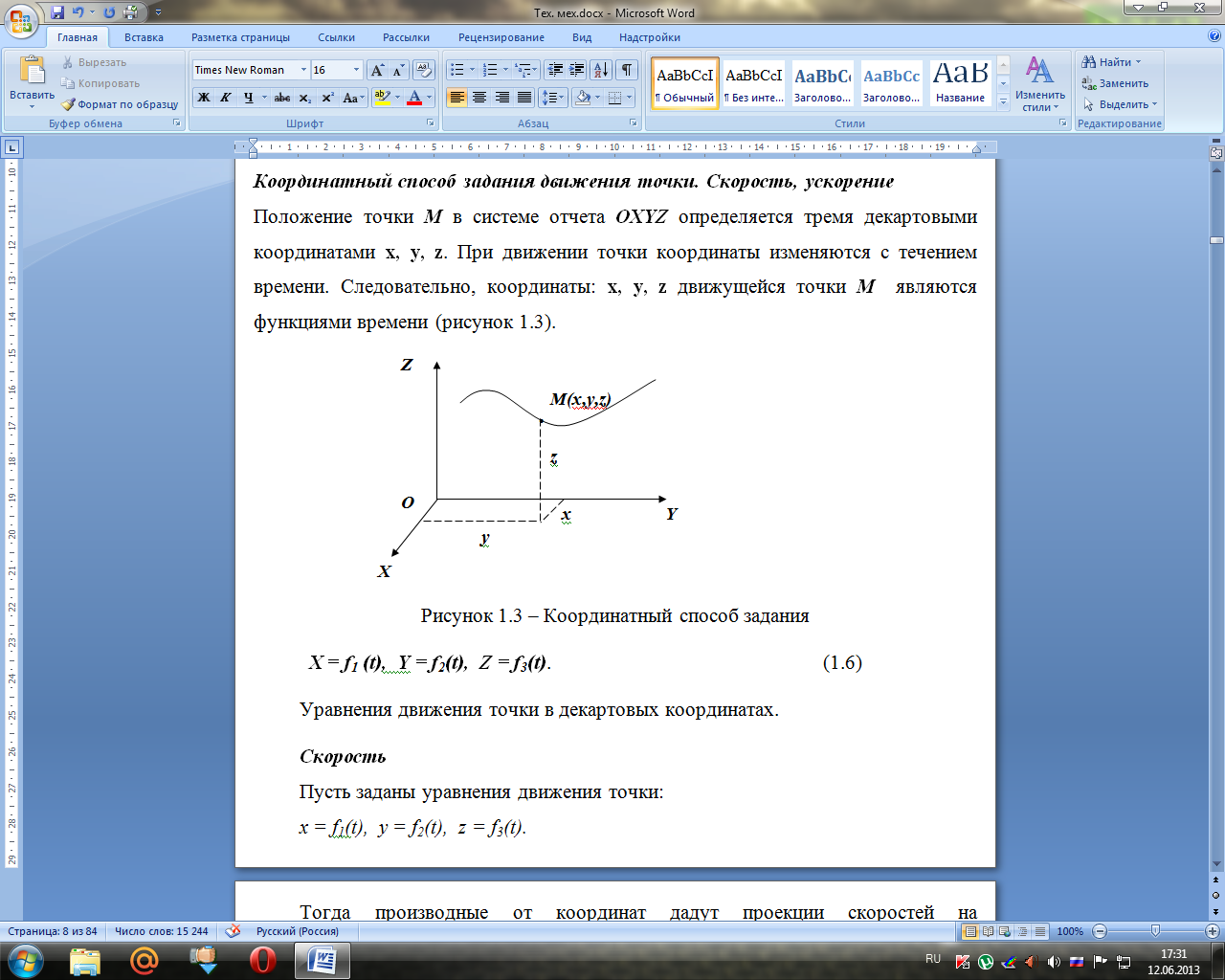
Рисунок 1.3 – Координатный способ задания
X = f1 (t), Y = f2(t), Z = f3(t). (1.6)
Уравнения движения точки в декартовых координатах.
Скорость
Пусть заданы уравнения движения точки:
x = f1(t), y = f2(t), z = f3(t).
Тогда производные от координат дадут проекции скоростей на координатные оси:
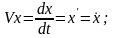
 (1.7)
(1.7)

Модуль скорости и направление определяются следующими формулами (рисунок 1.4):
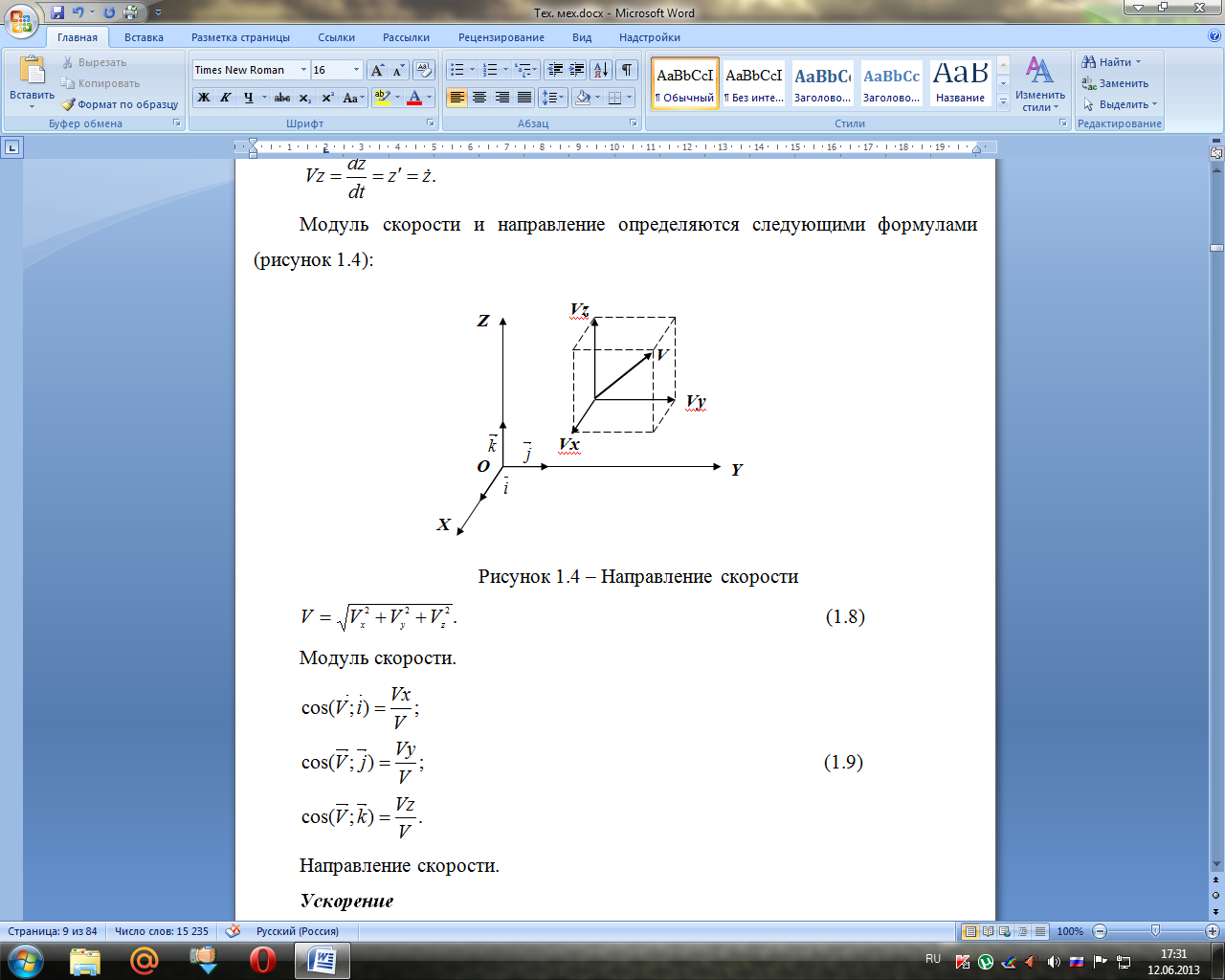
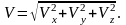 (1.8)
(1.8)
Модуль скорости.
 (1.9)
(1.9)
Направление скорости.
Ускорение
Проекции ускорения на координатные неподвижные оси декартовых координат, равны вторым производным от соответствующих координат точки по времени или первым производным по времени от проекции скорости на соответствующие оси.

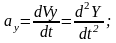 (1.10)
(1.10)
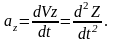
Модуль ускорения и направление определяются следующими формулами:
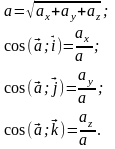 (1.12)
(1.12)
Естественный способ задания движения точки. Скорость, ускорение
При естественном способе задания движения точки известны: траектория АВ, начало и направление отчета дуговой координаты О и уравнение движения точки S = f(t) (рисунок 1.5).
S = OM, MM1 = ∆S.
Тогда: S1 = OM1 = OM + MM1 = S + ∆S. (1.13)
Скорость
Скорость в данном случае определится:
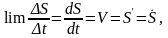 (1.14)
(1.14)
при ∆t→0.
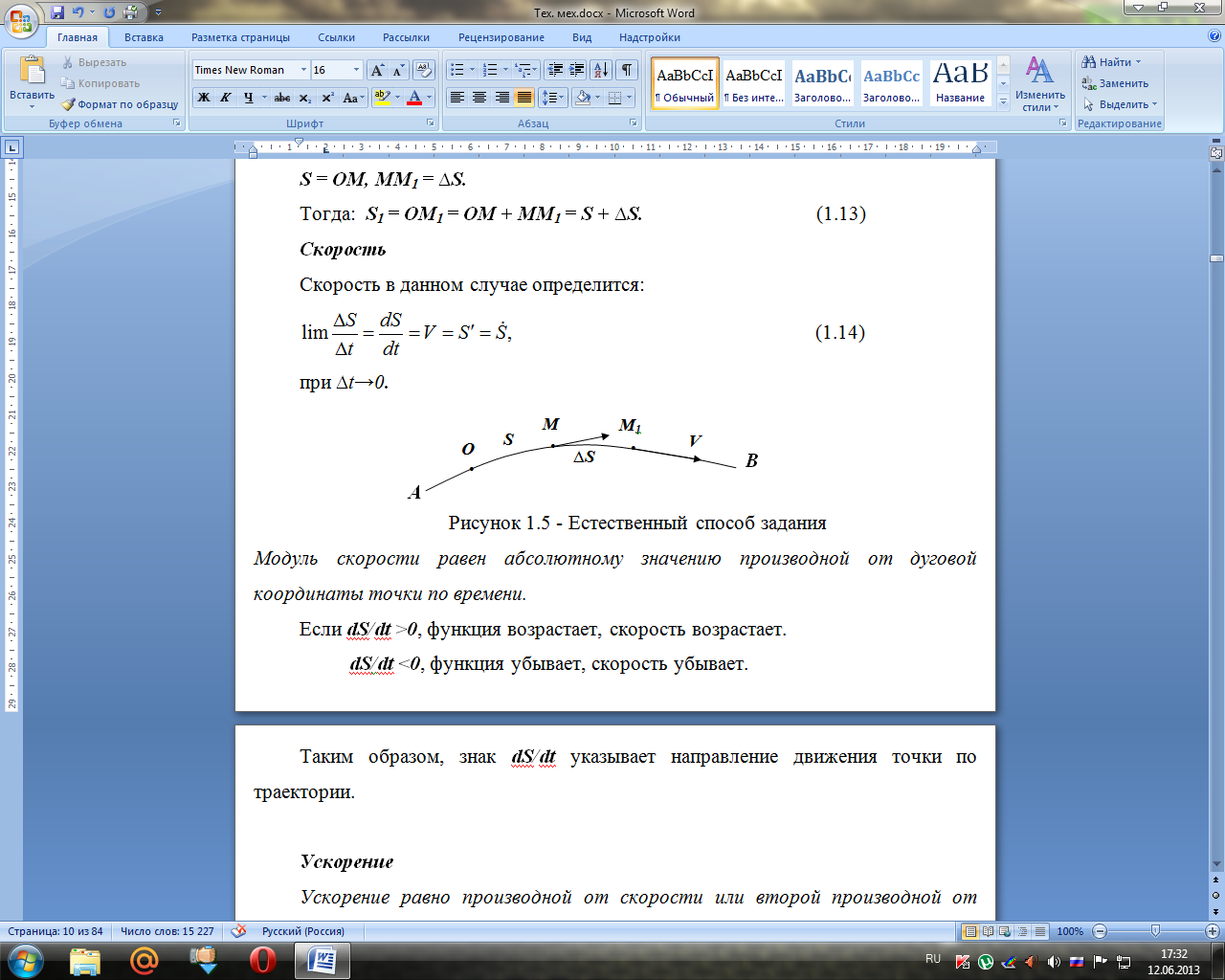
Рисунок 1.5 - Естественный способ задания
Модуль скорости равен абсолютному значению производной от дуговой координаты точки по времени.
Если dS/dt >0, функция возрастает, скорость возрастает.
dS/dt <0, функция убывает, скорость убывает.
Таким образом, знак dS/dt указывает направление движения точки по траектории.
Ускорение
Ускорение равно производной от скорости или второй производной от дуговой координаты точки по времени.
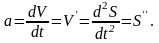 (1.15)
(1.15)
Естественный способ задания движения точки применяется в случае, когда траектория точки заранее известна. При этом траекторией может быть как прямая, так и кривая линия.
Движение точки определено если известны следующие элементы: траектория точки, начало и направление отчета, и уравнение движения S=f(t) .
8.
Касательное и нормальное ускорения
Определим проекции ускорения точки на естественные координатные оси.
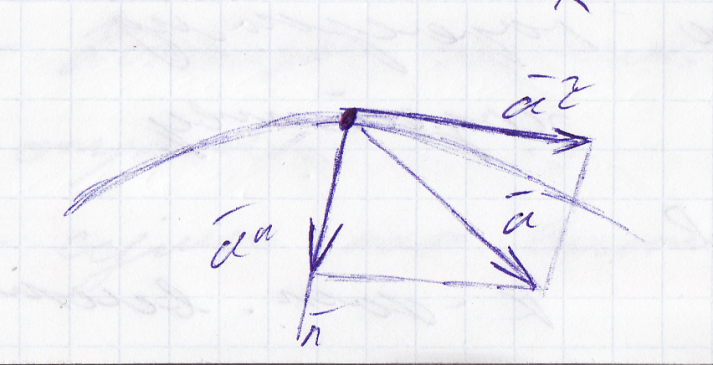
Вектор
скорости:
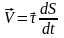 .
.
 (1.16)
(1.16)
Первое слагаемое умножим на 1 = dS/dS, а во втором
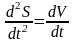 произведем замену.
произведем замену.
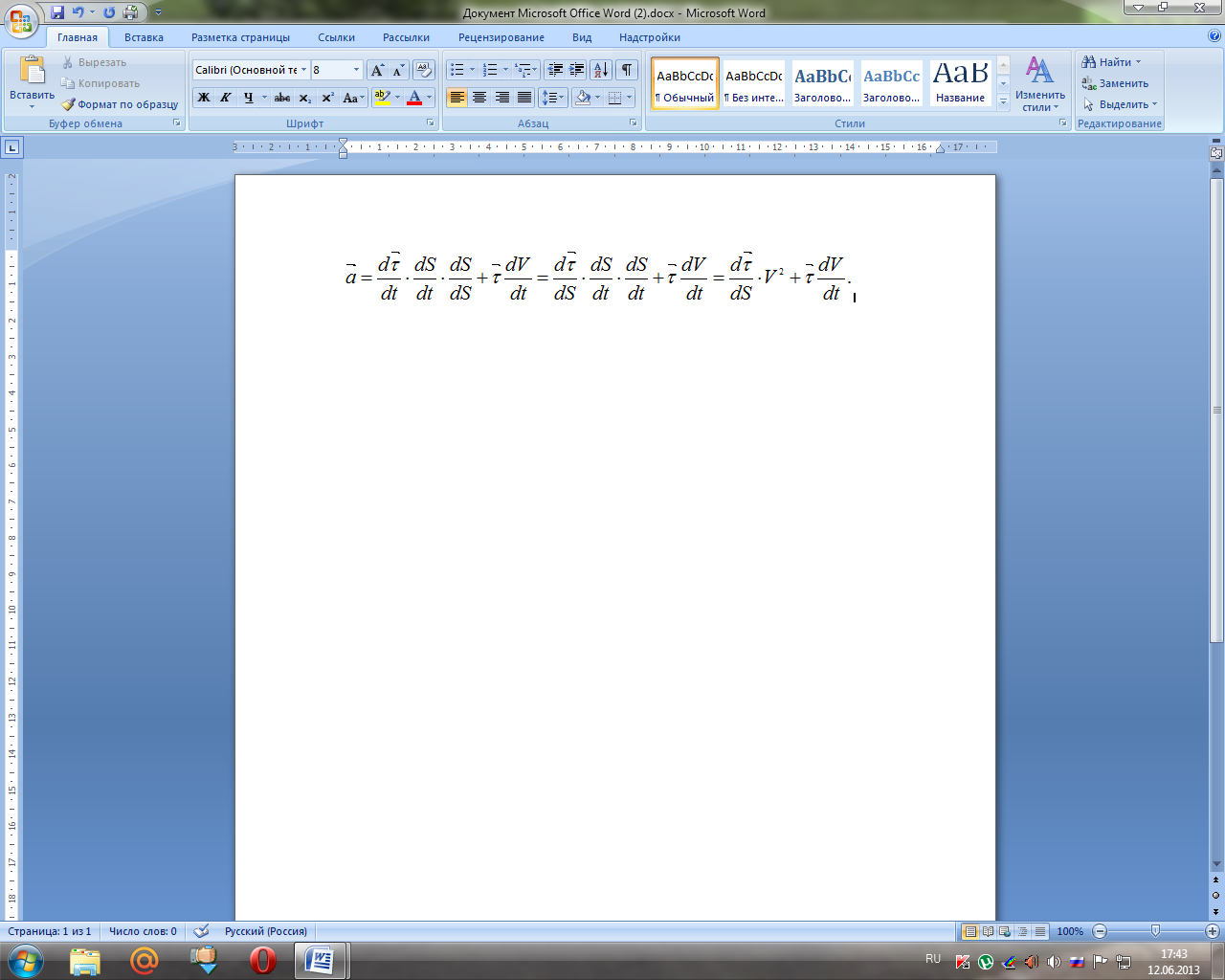

где
 - кривизна;
- кривизна;
ρ – радиус кривизны;
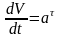 -касательное
ускорение.
-касательное
ускорение.
Тогда:
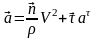 ,
или
,
или
 .
(1.18)
.
(1.18)
Ускорение точки равно геометрической сумме двух ускорений: нормальному, направленному по главной нормали и касательному, направленному по касательной к траектории движения точки.
Проекция ускорения точки на главную нормаль, равна квадрату модуля скорости точки, деленному на радиус кривизны в соответствующей точке.
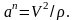 (1.19)
(1.19)
Проекция ускорения точки на касательную, равна производной от алгебраической величины скорости по времени.
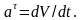 (1.20)
(1.20)
Следовательно, ускорение определится по зависимости:
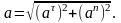 (1.21)
(1.21)
Направление:
 (1.22)
(1.22)
Радиус кривизны определяется:
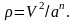
9.
Линейная скорость и ускорение при вращательном движении
Вектор угловой скорости (псевдовектор) направлен вдоль оси в ту сторону, что бы смотреть с положительного направления оси и видеть вращение против хода часовой стрелки (рисунок 3.2).
Скорость определяется, как вектор векторного произведения.
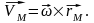 (3.7)
(3.7)
Определим ускорение:
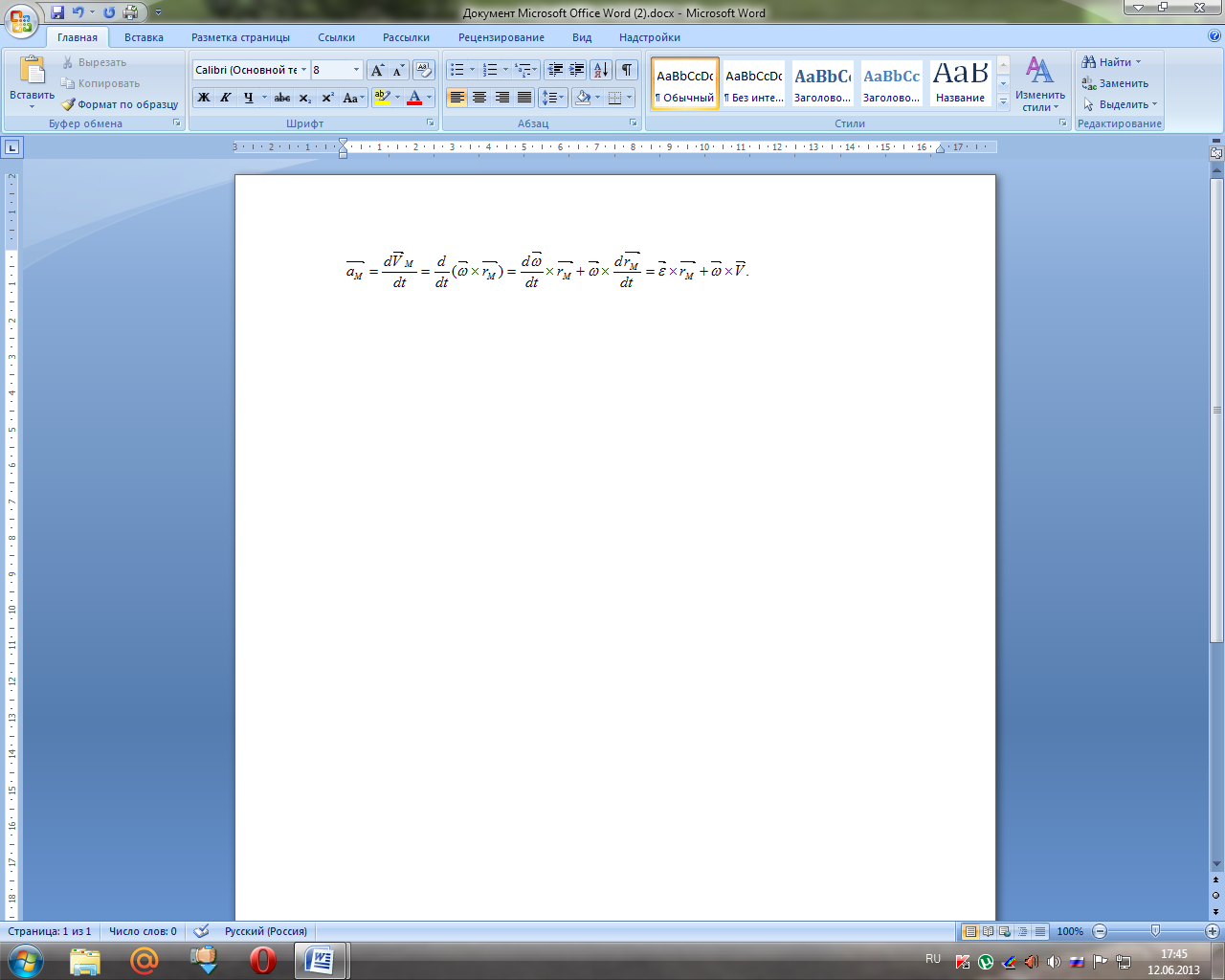
 (3.8)
(3.8)
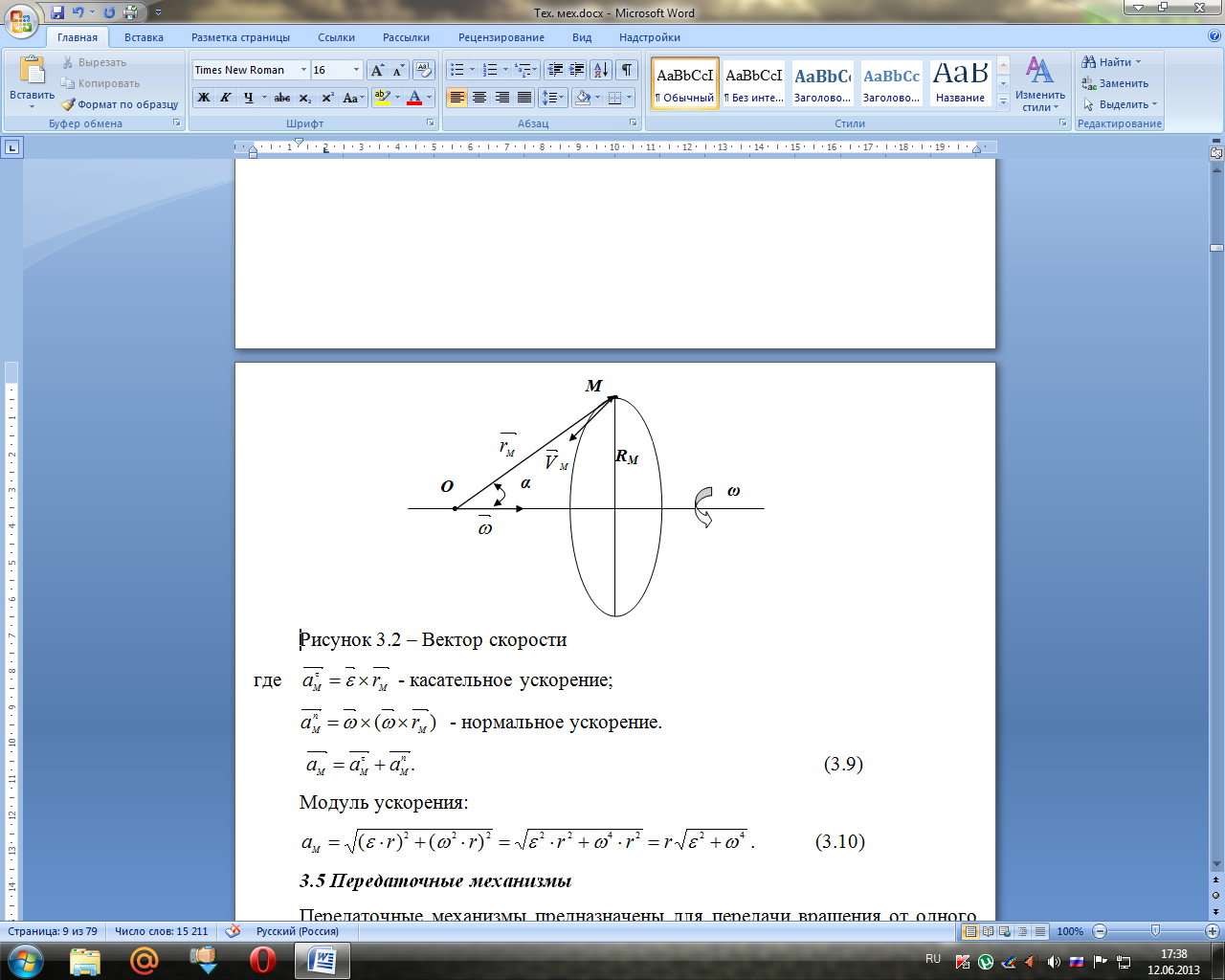
Рисунок 3.2 – Вектор скорости
где
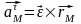 - касательное ускорение;
- касательное ускорение;
 - нормальное
ускорение.
- нормальное
ускорение.
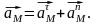 (3.9)
(3.9)
Модуль ускорения:
![]()
