Mинистерство образования и науки Украины

Донецкий национальный технический университет

Методические указания

к выполнению курсовой работы по дисциплине «Электротехника» для студентов специальности 7.090902 «Научные, аналитические, экологические приборы и системы»

Донецк, 2010

Методические указания к выполнению курсовой работы по дисциплине «Электротехника» для студентов специальности 7.090902 «Научные, аналитические, экологические приборы и системы». – Донецк: ДонНТУ, 2010. – 18 с.

В методических указаниях содержатся задания и варианты данных к ним по курсовой работе, охватывающей основные разделы дисциплины «Электротехника», приведены основные теоретические положения и методика выполнения заданий.

Составители: В.Ф. Сенько, доц.

А.Г. Лыков, асс.

Задание на курсовую работу содержит две независимые части, охватывающие основные разделы дисциплины «Электротехника».

Часть 1.

Из заданного напряжения несинусоидальной формы U(t) с помощью полосового фильтра выделить напряжение определенной гармоники. Коэффициент гармоник выходного напряжения не должен превышать заданного значения К_г. Для полученной схемы построить логарифмическую амплитудно-частотную характеристику (ЛАЧХ), по которой проверить полученные результаты.

Исходные данные к расчету:

форма и параметры входного напряжения (U_m, T, t_u);

номер выделяемой гармоники (n = 1, 2 или 3);

коэффициент гармоник К_г.

Выделение определенной гармонической составляющей из напряжения несинусоидальной формы осуществляется за счет зависимости полного сопротивления параллельного колебательного контура от частоты. Как известно, на резонансной частоте сопротивление параллельного колебательного контура максимально и в пределах полосы пропускания модуль сопротивления уменьшается не более чем в 1,41 раза. За пределами полосы пропускания сопротивление контура резко уменьшается, поэтому при прохождении через контур токов различных частот на контуре будут выделяться падения напряжений с частотами, лежащими в пределах полосы пропускания. Если ток через контур обусловлен несинусоидальным напряжением, т.е. напряжением, которое согласно теореме Фурье может быть представлено рядом гармонических составляющих с частотами, кратными основной частоте, то за счет выбора соответствующей полосы пропускания контура можно добиться того, что контур будет представлять большое сопротивление для токов только одной частоты, а для остальных частот сопротивление контура будет незначительным, вследствие чего напряжение на контуре будет определяться током гармонической составляющей, частота которой равна резонансной частоте контура (см. рис. 1). Форма напряжения на контуре будет практически синусоидальной, а падения напряжения от токов других гармоник будут незначительными и их влияние на форму выходного напряжения оценивается коэффициентом гармоник К_г. В зависимости от номера выделяемой гармоники К_г определяется следующим образом:

- при выделении первой гармоники;

- при выделении второй гармоники;

- при выделении третьей гармоники.

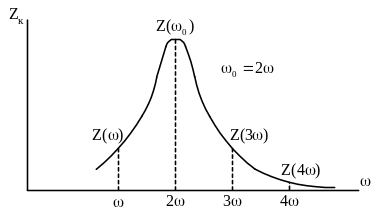
Рис. 1

Поэтому для выполнения поставленного задания необходимо определить гармонический состав заданного напряжения и рассчитать параметры параллельного колебательного контура, обеспечивающего требуемую для получения заданного коэффициента гармоник эквивалентную добротность контура.

Определение гармонического состава заданного напряжения производится с помощью разложения в ряд Фурье. В данной работе разложение в ряд Фурье можно ограничить четырьмя гармоническими составляющими. При разложении заданного напряжения в ряд Фурье целесообразно использовать перенос системы координат (или отдельно оси времени и оси напряжения) для упрощения общего выражения ряда Фурье. Перенос оси абсцисс (оси времени) производится в том случае, если в результате переноса форма заданного напряжения будет симметрична либо относительно оси времени, либо относительно начала координат. В зависимости от вида симметрии в разложении в ряд Фурье будут отсутствовать либо четные гармоники, либо косинусные составляющие. Перенос оси ординат (оси напряжений) целесообразен тогда, когда после переноса форма напряжения будет симметрична относительно оси ординат. В этом случае в разложении в ряд Фурье будут отсутствовать синусные составляющие.

Эквивалентная добротность параллельного колебательного контура всегда меньше конструктивной добротности контура, так как в любой электрической цепи контур шунтируется различными сопротивлениями, например, сопротивлением нагрузки или внутренним сопротивлением источника напряжения. Для того, чтобы эквивалентная добротность контура равнялась конструктивной, необходимо, чтобы внутреннее сопротивление источника было бы равно бесконечности, т.е. подключать контур к источнику тока. При подключении контура к источнику напряжения внутреннее сопротивление источника увеличивается искусственно, за счет включения дополнительного сопротивления последовательно с контуром. С учетом этого схема для выделения определенной гармоники с помощью параллельного колебательного контура имеет вид, показанный на рис. 2 (внутренним сопротивлением источника e(t) пренебрегаем). За счет падения напряжения на дополнительном сопротивлении амплитуда напряжения на контуре будет меньше, чем амплитуда соответствующей гармонической составляющей в исходном напряжении, но определяющим в таких случаях является гармонический состав напряжения на контуре.

Конструктивная добротность контура определяется параметрами колебательного контура:

Эквивалентная добротность контура (с учетом сопротивлений, шунтирующих контур) определяется в основном вносимым в контур активным сопротивлением:

С учетом вносимого в контур сопротивления схему рис.2 можно заменить на схему рис.3, где:

Согласно схемы рис.3 напряжение на контуре U_ab от действия каждой гармоники входного напряжения определяется по закону Ома:

Для небольших отклонений частоты сигнала Δω от резонансной частоты контура ω₀ сопротивление контура определяется по формуле:

где - обобщенная расстройка контура.

На границе полосы пропускания контура Q_экв∙а=1, за пределами полосы пропускания |Q_экв∙а|≥1 и при а>0.5 произведение Q_экв∙а значительно больше единицы, поэтому модуль комплексного числа (1+Q_экв∙а) практически равен Q_экв∙а. Следовательно, если на резонансной частоте ω₀ сопротивление контура равно:

то для ближайших гармонических составляющих сопротивление контура уменьшится в Q_экв∙а раз:

где

Для выделения заданной гармонической составляющей резонансная частота контура выбирается равной частоте этой гармоники. Поэтому падение напряжения на контуре на этой частоте равно:

Для ближайшей гармонической составляющей (или двух составляющих при n = 2; 3) аналогично получим:

Значение эквивалентной добротности необходимо выбирать таким, чтобы амплитуды смежных гармонических составляющих были бы не менее чем в 1/К_г раз меньше, чем амплитуда выделяемой гармоники. Исходя из этого условия для всех гармонических составляющих, кроме выделяемой, определяется требуемое значение эквивалентной добротности и из полученных значений Q_эквi выбирается наибольшее. При больших значениях а>0.5 определение Q_экв производится с погрешностью, поэтому выбранное значение Q_экв рекомендуется увеличить на (20÷25) %.

Конструктивная добротность контура Q_к всегда больше Q_экв. Для частот порядка десятков-сотен килогерц величина конструктивной добротности не превышает 100 – 150. Исходя из этого, при выборе элементов контура задаются значением Q_к и определяют параметры элементов колебательного контура. Номинал одного из элементов (L или С) можно выбрать произвольно, руководствуясь практическими соображениями. Обычно задаются емкостью конденсатора С. На частотах порядка сотен килогерц емкость конденсатора выбирают не менее 1000 пФ, по мере уменьшения частоты емкость конденсатора увеличивается. После выбора емкости конденсатора определяют параметры индуктивности контура:

Требуемое значение сопротивления резистора R_доп определяется на основании того, что за счет вносимого в контур активного сопротивления, обусловленного этим резистором, добротность контура в схеме должна быть не менее Q_{экв .}

Для построения ЛАЧХ необходимо по схеме рис.2 получить выражение коэффициента передачи K(jω), считая напряжение на контуре выходным. Согласно рис.2 схему можно упростить, введя сопротивление контура Z_K(jω) (см. рис.4).

Рис.4

Тогда:

где

Коэффициент передачи схемы равен:

Чтобы получить удобное для построения ЛАЧХ выражение K(ω), полученное выражение K(jω) необходимо привести к виду:

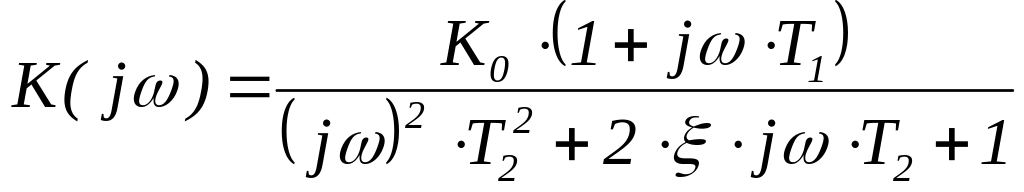
Модуль K(ω) записывается в виде:

и выражение для ЛАЧХ имеет вид:

Асимптотическая ЛАЧХ состоит их трех участков, границами участков являются частоты:

На первом участке 0< ω≤ ω_ср1 величины ω∙Т₁ и ω∙Т₂ меньше единицы, поэтому:

1.

На втором участке ω_ср1 ≤ ω≤ ω_ср2 величины ω∙Т₁ >1, ω∙Т₂ <1, поэтому:

2.

и второй участок представляет собой прямую, проходящую с наклоном +20 дб/дек.

На третьем участке ω_ср1 ≤ ω< ∞ величины ω∙Т₁ и ω∙Т₂ больше единицы, поэтому:

3.

В точке ω = ω_ср2 наклон ЛАЧХ изменяется на -40 дб/дек, поэтому третий участок на координатной плоскости проходит с наклоном -20 дб/дек.

Для получения реальной ЛАЧХ вносится коррекция: в точке изменения наклона ЛАЧХ на 20 дб/дек на частоте среза вносится поправка 3 дб в сторону излома и 1 дб на частотах ω_ср1/2 и 2∙ω_ср1; в точке изменения наклона на -40 дб/дек (ω_ср2) коррекция вносится в зависимости от величины ξ, которая определяется из выражения K(jω). Величины коррекции для различных значений ξ приведены на рис.5.

Рис.5

После внесения коррекции производится проверка полученных ранее значений U(ω₀) и Q_экв по построенной ЛАЧХ.

Для нахождения U(ω₀) по ЛАЧХ определяется значение 20∙lgK(ω_ср2), затем находится величина K(ω_ср2) и выходное напряжение:

Для проверки значения Q_экв определяют границы полосы пропускания ω₁ и ω₂ . Для этого значение L(ω_ср2) уменьшают на 3 дб и таким образом получают частоты ω₁ и ω₂. Полоса пропускания равна П=(ω₁ - ω₂), а эквивалентная добротность:

Полученные значения U(ω₀) и Q_экв должны отличаться от ранее полученных не более чем на 20%.

Данные для выполнения задания приведены в таблице.

№№ /пп	Форма U	f, кГц	Um	n	Кг ,%
1	1	5	10	1	2,0
2	1	10	6	2	3,0
3	1	15	9	3	5,0
4	2	10	5	1	1,5
5	2	15	9	2	2,0
6	3	10	10	1	2,0
7	3	15	5	2	2,5
8	3	20	6	3	3,0
9	4	10	9	1	2,5
10	4	15	5	2	3,5
11	1	10	5	1	1,5
12	1	15	10	2	3,0
13	1	5	6	3	2,5
14	2	10	10	2	3,0
15	2	15	9	1	1,5
16	3	15	6	1	2,0
17	3	20	9	2	3,0
18	3	10	10	3	2,5
19	4	10	5	2	3,5
20	4	15	9	1	1,5
21	1	15	5	1	2,0
22	2	20	6	1	1,5
23	3	10	9	2	3,0
24	4	20	10	1	2,0
25	1	10	15	2	1,5

Формы входных напряжений представлены на рис. 6.

Рис. 6