Раздел 3.3. Альтернативная модель демографической политики
Также мы предлагаем свою модель, суть которой повышение интеллектуального уровня, но за счёт изменения поведения части женщин.
а) Предположим, что небольшой процент женщин рожает детей от самых умных мужчин и методом подбора определим их оптимальное количество. Начальными условиями являются: население (N0) 1000 человек, коэффициент выживания детей (Klife) 0.85, q – % женщин, рожающих детей от самых умных мужчин.
б) Вторая модель, используемая для сравнения, когда небольшой процент женщин рожает детей от абсолютно произвольной категории мужчин, не привязываясь к их интеллекту
Таблица 3.3.1.
q |
Nfin |
IQmax |
IQпик |
|||
|
Модель 2а |
Модель 2б |
Модель 2а |
Модель 2б |
Модель 2а |
Модель 2б |
0 |
6237 |
6315 |
120 |
128 |
50 |
50 |
0,001 |
6246 |
8178 |
165 |
132 |
60 |
50 |
0,003 |
9371 |
7953 |
265 |
141 |
70 |
50 |
0,005 |
6353 |
8616 |
292 |
127 |
70 |
50 |
0,007 |
7769 |
7842 |
362 |
142 |
70 |
50 |
0,01 |
8731 |
9402 |
488 |
206 |
70 |
60 |
0,02 |
8706 |
8076 |
565 |
227 |
70, 535 |
60 |
0,03 |
7099 |
7600 |
629 |
220 |
70, 600 |
60 |
0,05 |
4081 |
5387 |
636 |
233 |
70, 610 |
60 |
0,07 |
4008 |
5794 |
730 |
266 |
70, 700 |
60 |
0,1 |
2406 |
3433 |
736 |
275 |
70, 700 |
60 |
0,2 |
146 |
1270 |
653 |
350 |
70, 630 |
60 |
0,3 |
66 |
229 |
621 |
307 |
70, 610 |
60 |
Снижение численности населения с увеличением % женщин, рожающих детей от самых умных мужчин характеризуется статистическими данными, по которым нет женщин с детьми с IQ выше 121.
Ниже приведены графики результата эволюционного моделирования для случая q=0.3, графики зависимости конечной численности населения (Nfin) от % женщин, рожающих детей от самых умных мужчин (q) и максимального уровня интеллекта (IQmax) от % женщин, рожающих детей от самых умных мужчин (q).
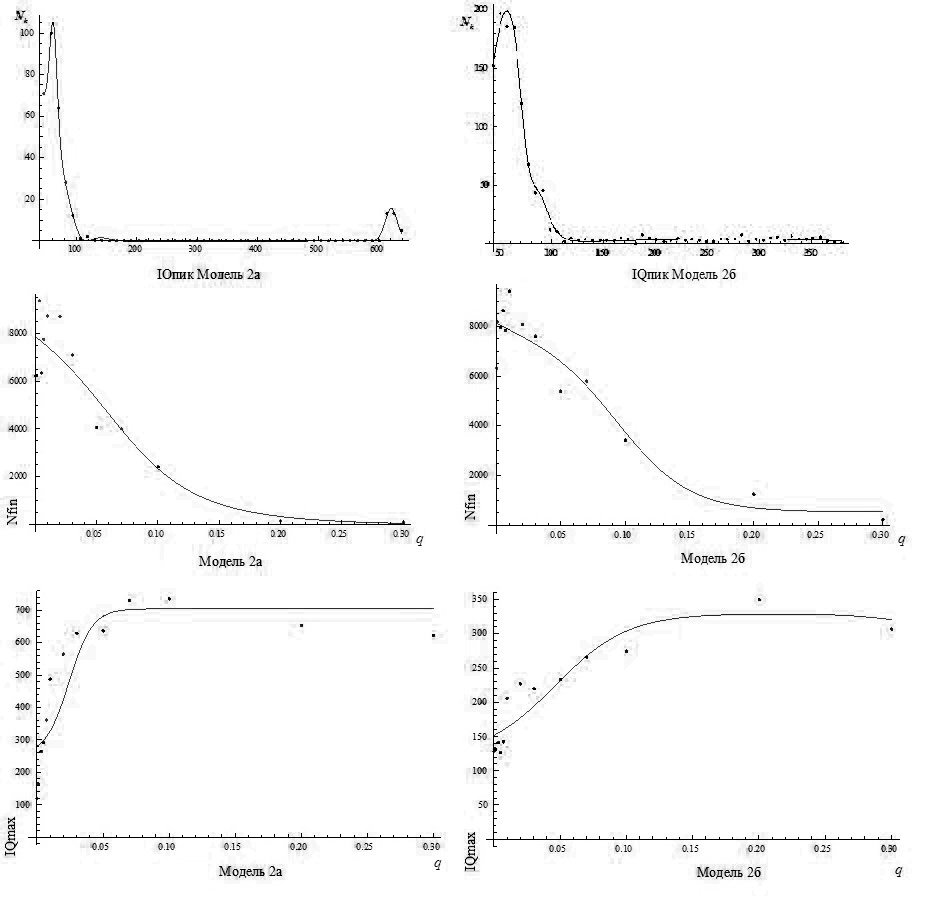
Рис. 3.3.1. Графики результатов исследования
Оба варианта второй модели показывают схожие результата, однако в первой модели (2а) наблюдается существенно большее возрастание уровня интеллекта и второе распределение (пиковое значение) на достаточно высоком уровне интеллекта (535-700).
Проведённое исследование показывает, что мягкое воздействие на эволюционную динамику, которое можно проводить воздействием на морально-этическую систему приводит к более явным и сильным результатам, чем жёсткое регулирование, характерное для сингапурской модели. Однако, социум, получающийся в результате, оказывается менее однородным, что должно привести к труднорешаемым социальным проблемам.
Модель 3. Программа построения зависимости рождаемости в РФ от интеллекта в зависимости от q.
N1=1000;m=50;m1=5;m2=30;m3=0;p=1;q=0.1;Mo=100;=20;r=0.4;1=10;klife=0.9;
S=0.5;xc=1.1398763664584803;a=0.3782965773803407;c=-12.934335930675283;
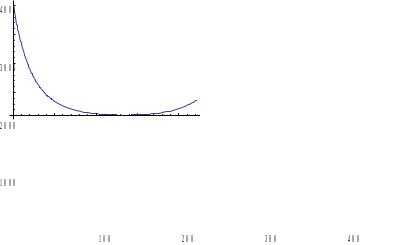
R[x_]:=Max[c Tanh[a(x/100-xc)]+S,0]
Plot[R[x],{x,0, 200},PlotRangeAll]
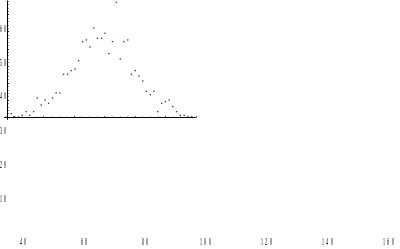
X=RandomReal[NormalDistribution[Mo,], N1];
Y=Sort[X];
Z=Table[Y[[1]]+(Y[[N1]]-Y[[1]])(i-1)/m,{i,m+1}];
F=Table[Length[Select[X,Z[[i]]<#<Z[[i+1]]&]],{i,m}];
Z1=Z+(Y[[N1]]-Y[[1]])/(2m);
Z2=Delete[Z1,-1];
ListPlot[Table[{Z2[[n]],F[[n]]},{n,m}]]
Do[X1={};Do[Do[Do[If[RandomReal[]<(2-q) klife R[Z1[[k]]]/20,x=RandomReal[NormalDistribution[Z1[[k]],1]];If[x>Mo r,X1=Append[X1,x],Null],Null];If[RandomReal[]<q klife R[Z1[[k]]]/20,x=RandomReal[NormalDistribution[Z1[[RandomInteger[{1,m}]]],1]];If[x>Mo r,X1=Append[X1,x],Null],Null],{i,Length[Select[X,Z[[k]]<#<Z[[k+1]]&]]}],{k,m3+1,m}],{i,m1}];
X=X1;N1=Length[X];
Y=Sort[X];Z=Table[Y[[1]]+(Y[[N1]]-Y[[1]])(i-1)/m,{i,m+1}];F=Table[Length[Select[X,Z[[i]]<#<Z[[i+1]]&]],{i,m}];
Z1=Z+(Y[[N1]]-Y[[1]])/(2m);Z2=Delete[Z1,-1];g=ListPlot[Table[{Z2[[n]],F[[n]]},{n,m}],PlotRangeAll]; Print[g]; Print[Z1[[m]]]; Print[N1];Print[j],{j,m2}];
n1=1;n=5;=0.01;
u[x_,xc_,a_,c_]:=c Exp[-a (x-xc)2]
gx[x_,xc_,a_,c_]:=2a c (x-xc)Exp[-a (x-xc)2]
ga[x_,xc_,a_,c_]:=-c (x-xc)2 Exp[-a (x-xc)2]
gc[x_,xc_,a_,c_]:= Exp[-a (x-xc)2]
Do[Xg[i]=Z2[[i]]/100,{i,m}]
Do[G[i]=F[[i]]/100,{i,m}]
X=Table[Xg[i],{i,m}]
{0.440659,0.521956,0.603252,0.684549,0.765846,0.847143,0.92844,1.00974,1.09103,1.17233,1.25363,1.33492,1.41622,1.49752,1.57881,1.66011,1.74141,1.82271,1.904,1.9853,2.0666,2.14789,2.22919,2.31049,2.39178,2.47308,2.55438,2.63567,2.71697,2.79827,2.87956,2.96086,3.04216,3.12346,3.20475,3.28605,3.36735,3.44864,3.52994,3.61124,3.69253,3.77383,3.85513,3.93642,4.01772,4.09902,4.18031,4.26161,4.34291,4.4242}
xmin=Min[X];xmax=Max[X];
gr1:=ListPlot[g,PlotRangeAll];gr2:=Plot[us[x,jmin[[1]]],{x,xmin,xmax},PlotRangeAll];
Do[L[i,1,1]=xmin+(xmax-xmin)Random[],{i,n}]
Do[L[i,1,2]= Random[],{i,n}]
Do[L[i,1,3]=Random[],{i,n}]
Do[Do[L[i,j,1]=L[i,1,1]+ (xmax-xmin)(2*Random[]-1),{i,n}],{j,2,n1}]
Do[Do[L[i,j,2]=L[i,1,2]+ *(2*Random[]-1),{i,n}],{j,2,n1}]
Do[Do[L[i,j,3]=L[i,1,3]+ (2*Random[]-1),{i,n}],{j,2,n1}]
us[x_,j_]:=
=Table[
,{j,n1}]
{7620.85}
jmin=Ordering[-,-1]
{1}
=
/
3.31201
Do[Do[L[i,j,3]=L[i,j,3],{i,n}],{j,1,n1}]
Plot[us[x,jmin[[1]]],{x,xmin,xmax},PlotRangeAll]
g=Table[{Xg[i],G[i]},{i,m}];Print[gr1]
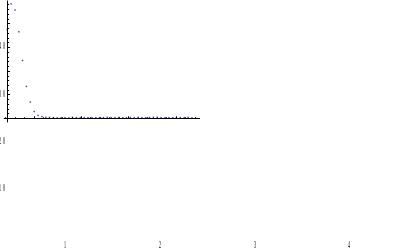
Do[Do[g[k,j]=us[Xg[k],j]-G[k],{k,m}],{j,n1}];
Do[Do[Gxc[i,j]=
;
Gc[i,j]=
;
Ga[i,j]=
,{i,n}],{j,n1}];
Do[GxcS[i]= Sum[Gxc[i,j],{j,n1}]/n1;GcS[i]= Sum[Gc[i,j],{j,n1}]/n1;GaS[i]= Sum[Ga[i,j],{j,n1}]/n1,{i,n}];
0=-0.000001;1=1.2;2=0.5;K1 =20;K=20;t=TimeUsed[];
Do[[j]=0,{j,n1}];
Do[xc[i]=0 GxcS[i];c[i]=0*GcS[i];a[i]=0*GaS[i],{i,n}];
Do[Pxc[i]=GxcS[i];Pc[i]=GcS[i];Pa[i]=GaS[i],{i,n}];
Do[Do[L[i,j,1]=L[i,j,1]+xc[i],{i,n}];Do[L[i,j,2]=L[i,j,2]+a[i],{i,n}];Do[L[i,j,3]=L[i,j,3]+c[i],{i,n}],{j,n1}];
Do[
Do[
Do[Do[g[k,j]=us[Xg[k],j]-G[k],{k,m}],{j,n1}];
Do[Do[Gxc[i,j]= ;
Gc[i,j]= ;
Ga[i,j]= ,{i,n}],{j,n1}];
Do[GxcS[i]= Sum[Gxc[i,j],{j,n1}]/n1;GcS[i]= Sum[Gc[i,j],{j,n1}]/n1;GaS[i]= Sum[Ga[i,j],{j,n1}]/n1,{i,n}];
Do[xc[i]=If[Pxc[i]*GxcS[i]>0,1*xc[i],-2*xc[i]];c[i]=If[Pc[i]*GcS[i]>0,1*c[i],-2*c[i]];a[i]=If[Pa[i]*GaS[i]>0,1*a[i],-2*a[i]],{i,n}];
Do[Pxc[i]=GxcS[i];Pc[i]=GcS[i];Pa[i]=GaS[i],{i,n}];
Do[Do[L[i,j,1]=L[i,j,1]+xc[i],{i,n}];Do[L[i,j,2]=L[i,j,2]+a[i],{i,n}];Do[L[i,j,3]=L[i,j,3]+c[i],{i,n}],{j,n1}];
Do[Do[g[k,j]=us[Xg[k],j]-G[k],{k,m}],{j,n1}];
=Table[
,{j,n1}],{i3,K}];
jmin=Ordering[];t=TimeUsed[]-t;t=TimeUsed[];max=
Table[
,{i,m}];fin=[[jmin[[1]]]];Print["min=",[[jmin[[1]]]],"
","jmin=",jmin[[1]]," ","max=",[[jmin[[n1]]]],"
","сA=",L[n,1,3],"
","=",
,"
","i4=",i4," ","n=",n,"
","t=",t];Do[Print[L[i,1,2]],{i,n}];g=Table[{Xg[i],G[i]},{i,m}];gr5=Show[gr1,gr2];Print[gr5],{i4,K1}]
M[l_,k_]:=
;
M1=Array[M,{n,n}];
B=Table[
,{l,n}];
Z1=LinearSolve[M1,B];Do[L[i,jmin[[1]],3]=Z1[[i]],{i,n}];
Do[Do[g[k,j]=us[Xg[k],j]-G[k],{k,m}],{j,n1}];=Table[ ,{j,n1}];jmin=Ordering[];t=TimeUsed[]-t;t=TimeUsed[];
Print["min=",[[jmin[[1]]]]];
min=_5.99289
Print["jmin=",jmin[[1]]];
jmin=_1
Print["сA=",L[n,jmin[[1]],3]];
сA=_36.4019
Print["=", ];
=_0.346205
Print[" ","t=",t];
_t=_0.094
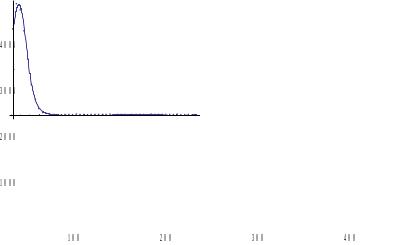
g=Table[{100Xg[i],100G[i]},{i,m}];
gr3:=Plot[100us[x/100,jmin[[1]]],{x,100xmin,100xmax},PlotRangeAll];
Show[gr1,gr3,PlotRangeAll]
Do[Print[100L[i,jmin[[n1]],1]],{i,n}]
510.55
436.523
68.4142
268.672
55.5512
Do[Print[L[i,jmin[[n1]],2]],{i,n}]
0.807099
-0.131417
16.1186
-0.404951
22.7164
Do[Print[L[i,jmin[[n1]],3]],{i,n}]
-8.2073
-1.24278
8.43668
2.17504
36.4019
Do[gr4=Plot[100u[x/100,L[i,jmin[[n1]],1],L[i,jmin[[n1]],2],L[i,jmin[[n1]],3]],{x,0,100xmax},PlotRangeAll];Print[gr4],{i,n}]
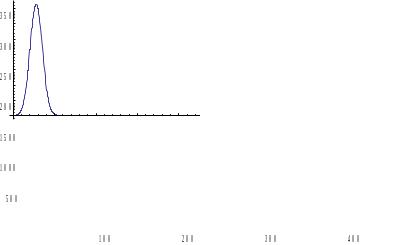
Table[{Z2[[n]],F[[n]]},{n,m}]
{{44.0659,3742},{52.1956,4824},{60.3252,4560},{68.4549,3650},{76.5846,2432},{84.7143,1342},{92.844,680},{100.974,282},{109.103,114},{117.233,71},{125.363,33},{133.492,30},{141.622,21},{149.752,16},{157.881,29},{166.011,25},{174.141,17},{182.271,34},{190.4,23},{198.53,22},{206.66,21},{214.789,26},{222.919,25},{231.049,26},{239.178,22},{247.308,24},{255.438,34},{263.567,18},{271.697,25},{279.827,33},{287.956,24},{296.086,20},{304.216,32},{312.346,22},{320.475,31},{328.605,22},{336.735,20},{344.864,34},{352.994,31},{361.124,30},{369.253,29},{377.383,26},{385.513,28},{393.642,19},{401.772,34},{409.902,20},{418.031,20},{426.161,32},{434.291,11},{442.42,6}}