1. Ряды динамики: определения, показатели (абсолютные приросты, темпы роста и прироста)

Ряды динамики — это ряды статистических показателей, характеризующих развитие явлений природы и общества во времени. Публикуемые Госкомстатом России статистические сборники содержат большое количество рядов динамики в табличной форме. Ряды динамики позволяют выявить закономерности развития изучаемых явлений.

бсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения.

Абсолютный прирост (базисный)

где yi - уровень сравниваемого периода; y0 - уровень базисного периода.

Абсолютный прирост с переменной базой (цепной), который называют скоростью роста,

где yi - уровень сравниваемого периода; yi-1 - уровень предшествующего периода.

Средний абсолютный прирост (средняя скорость роста) определяется как средняя арифметическая из показателей скорости роста за отдельные периоды времени:

где yn - конечный уровень ряда; y1 - начальный уровень ряда.

Темп роста 

Темп прироста ТП определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному.

Темп прироста базисный  

Темп прироста цепной

Темп прироста можно рассчитать и иным путем: как разность между темпом роста и 100 % или как разность между коэффициентом роста и 1 (единицей): 1) Тп = Тр - 100%; 2) Тп = Ki - 1.

Средний темп роста, %. Это средний коэффициент роста, который выражается в процентах:

Средний темп прироста  , %. Для расчета данного показателя первоначально определяется средний темп роста, который затем уменьшается на 100%. Его также можно определить, если уменьшить средний коэффициент роста на единицу: 

Абсолютное значение одного процента прироста Ai. Этот показатель служит косвенной мерой базисного уровня. Представляет собой одну сотую часть базисного уровня, но одновременно представляет собой и отношение абсолютного прироста к соответствующему темпу роста.

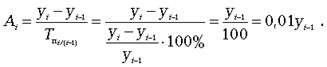
Среднее абсолютное значение 1% прироста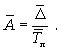 

2. Ряды динамики: определения, средние показатели,

Ряды динамики — это ряды статистических показателей, характеризующих развитие явлений природы и общества во времени. Публикуемые Госкомстатом России статистические сборники содержат большое количество рядов динамики в табличной форме. Ряды динамики позволяют выявить закономерности развития изучаемых явлений.

Каждый ряд динамики можно рассматривать как некую совокупность n меняющихся во времени показателей, которые можно обобщать в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении изменений того или иного показателя в разные периоды, в разных странах и т.д.

Обобщенной характеристикой ряда динамики может служить прежде всего средний уровень ряда. Способ расчета среднего уровня зависит от того, моментный ряд или интервальный (периодный).

В случае интервального ряда его средний уровень определяется по формуле простой средней арифметической величины из уровней ряда, т.е.

= Если имеется моментный ряд, содержащий n уровней (y1, y2, …, yn) с равными промежутками между датами (моментами времени), то такой ряд легко преобразовать в ряд средних величин. При этом показатель (уровень) на начало каждого периода одновременно является показателем на конец предыдущего периода. Тогда средняя величина показателя для каждого периода (промежутка между датами) может быть рассчитана как полусумма значений у на начало и конец периода, т.е. как  . Количество таких средних будет  . Как указывалось  ранее, для рядов средних величин средний уровень рассчитывается по средней арифметической. Следовательно, можно записать . После преобразования числителя получаем ,

где Y1 и Yn — первый и последний уровни ряда;   Yi  —  промежуточные уровни.

Эта средняя   известна в статистике как средняя хронологическая для моментных рядов. Такое название она получила от слова «cronos» (время, лат.), так как рассчитывается из меняющихся во времени показателей.

В случае неравных промежутков между датами среднюю хронологическую для моментного ряда можно рассчитать как среднюю арифметическую из средних значений уровней на каждую пару моментов, взвешенных по величине расстояний (отрезков времени) между датами, т.е. . В данном случае предполагается, что в промежутках между датами уровни принмали разные значения, и мы из двух известных (yi и yi+1) определяем средние, из которых затем уже рассчитываем общую среднюю для всего анализируемого периода. Если же предполагается, что каждое значение yi  остается неизменным до следующего (i+1)-го момента, т.е. известна  точная дата изменения уровней, то расчет можно осуществлять по формуле средней арифметической взвешенной: ,

где  – время, в течение которого уровень  оставался неизменным.

Кроме среднего уровня в рядах динамики рассчитываются и другие средние показатели – среднее изменение уровней ряда (базисным и цепным способами), средний темп изменения.

Базисное среднее абсолютное изменение представляет собой частное от деления последнего базисного абсолютного изменения на количество изменений. То есть

Б =

Цепное среднее абсолютное изменение уровней ряда представляет собой частное от деления суммы всех цепных абсолютных изменений на количество изменений, то есть

Ц =

По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность.

Из правила контроля базисных и цепных абсолютных изменений следует, что базисное и цепное среднее изменение должны быть равными.

Наряду со средними абсолютным изменением рассчитывается и среднее относительное тоже базисным и цепным способами.

Базисное среднее относительное изменение определяется по формуле

Б= = 

Цепное среднее относительное изменение определяется по формуле

Ц=

Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность. Вычитанием 1 из базисного или цепного среднего относительного изменения образуется соответствующий среднийтемп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики.

3.Ряды динамики: определения, составляющие. Выравнивание методом укрупнения интервалов.

Ряды динамики — это ряды статистических показателей, характеризующих развитие явлений природы и общества во времени. Публикуемые Госкомстатом России статистические сборники содержат большое количество рядов динамики в табличной форме. Ряды динамики позволяют выявить закономерности развития изучаемых явлений.

Динамика - процесс развития, движения социально-экономических явлений во времени.

Ряды динамики - последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления.

Основные элементы рядов динамики:

1) показатель времени - t (определенные даты времени или отдельные периоды);

2) уровни развития изучаемого явления - у.

Уровень рядов динамики - уровень, отражающий

количественную оценку развития во времени изучаемого явления.

Способы выражения уровней рядов динамики:

1) абсолютные величины;

2) относительные величины;

3) средние величины.

Классификация рядов динамики в зависимости от характера изучаемого явления:

1) моментные ряды;

2) интервальные ряды.

Моментные ряды динамики - ряды, отображающие состояние изучаемых явлений на определенные даты (моменты) времени. Суммирование уровней моментного ряда динамики не имеет смысла, так как одни и те же единицы совокупности обычно входят в состав нескольких уровней.

Интервальные ряды динамики - ряды, отображающие итоги развития изучаемых явлений за отдельные периоды (интервалы) времени. В интервальном ряду динамики уровни за примыкающие друг к другу периоды времени можно суммировать, получая итоги (уровни) за более продолжительные периоды.

Полный ряд динамики - ряд, в котором одноименные моменты времени или периоды времени строго следуют один за другим в календарном порядке.

Закономерности изменения явления во времени не проявляются в каждом конкретном уровне ряда. Это связано с действием на явления общих и случайных причин. Поэтому в статистике для выявления закономерности или тенденции развития явления используют следующие методы обработки рядов динамики:

1.    Метод сглаживания путем укрупнения интервалов во времени.

2.    Выравнивание рядов динамики методом скользящей средней.

3.    Метод аналитичного выравнивания.

Сущность приема укрепления интервалов сводится к следующему:

I прием. Первоначальный ряд динамики преобразуется и заменяется другим рядом, в котором показатели относятся к большим по продолжительности периодам времени, т.е. интервал укрупнен. Этот прием используется только для интервальных рядов динамики. Укрупнение производится до тех пор, пока не будет выявлена четкая тенденция развития явления, а уровни ряда охватывать большие периоды времени. Посмотрим на примере: имеются данные о производстве обуви за ряд лет (табл. 5.8), выявить тенденцию роста или снижения производства обуви методом укрепнения интервалов.

Таблица 5.8