2.1 Генератори сигналів інфранизьких частот

В момент включення генератора перед напругою на колекторі транзистора VT2 передається на засув польового транзистора VT1. Починається процес зарядки конденсатора С1. По мірі його зарядки напруга на колекторі транзистора VТ2 буде зменшуватися. Наступний момент, коли польовий транзистор вийде з насиченості і зменшить базовий ток транзистора VT2.

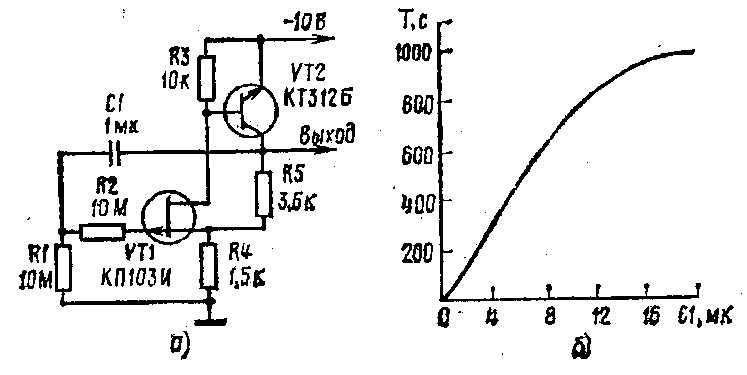
Рис. 7. а) Схема інфранизьких частот, б) Графік імпульсної температури

Швидкість зарядки конденсатора С1 різко зменшиться. В цьому випадку транзистор VT1 закриється і вслід за ним закриється транзистор VT2. Тепер починається процес розрядки конденсатора С1 через резистор R3. Позитивна напруга на конденсаторі підтримує закритим транзистор VT1 і залишається в цьому стані до повної розрядки конденсатора.

Період слідування імпульсів міняється на 1,5% (для Т=600с.) при зміні живлення на 11%. Для температури від +20 до +50С період міняється з коефіцієнтом 0,07% / С (рис. 4,б).

2.2 Генератори вимірювання сигналів низьких частот

Цифрові генератори низьких частот у порівнянні з аналоговими генераторами мають більш ефективні метрологічні характеристики. Зокрема, вони мають більш високу точність установки і стабільність частоти, малий коефіцієнт нелінійних перекручувань (строго синусоїдальної форми) і сталість рівня вихідного сигналу.

Цифрові генератори широко застосовуються, тому що в порівнянні з аналоговими вони більш зручні в експлуатації, мають високу швидкодію і наочну індикацію. У них істотно простіше встановлювати необхідну частоту. Крім того, у цифрових генераторах можна автоматично настроювати частоту по заздалегідь заданій програмі і можливо легке сполучення із цифровими засобами обробки інформації.

В основі принципу дії цифрових генераторів лежить формування числового коду з наступним перетворенням його в аналоговий гармонійний сигнал. Останній апроксимується функцією, модельованою за допомогою цифрового аналогового перетворювача (ЦАП).

Принципи апроксимації. Найпростіший вид апроксимації — східчаста (мал. 8, а). Вона полягає в заміні гармонійного коливання напругою східчастої форми, що досить мало відрізняється від синусоїдальної кривої. Пояснимо сутність східчастої апроксимації сигналів. Нехай апроксимуюча гармонійна напруга:

u(t) =Umaxsinwt

дискретизується за часом (при рівномірній дискретизації із кроком Δt) і в інтервалі, що розділяє два сусідніх моменти часу ti і ti+1. Це синусоїдальне коливання заміняють напругою постійного струму, тобто сходинкою, висота якої дорівнює значенню апроксимуючої напруги в момент ti, тобто:

У результаті такої заміни, замість кривої синусоїдальної форми виходить східчаста лінія, зображена на мал. 8, а.

При наявному періоді Т синусоїдального коливання число сходів р, що доводяться на один період, визначається кроком дискретизації

ρ = Τ/Δί.

Якщо ж з технічних міркувань число сходів задане, то зміна кроку дискретизації приводить до зміни періоду формованої напруги, оскільки

Τ = ρΔί.

Якщо tj = iΔt, то рівняння східчастої кривої можна представити в наступному виді:

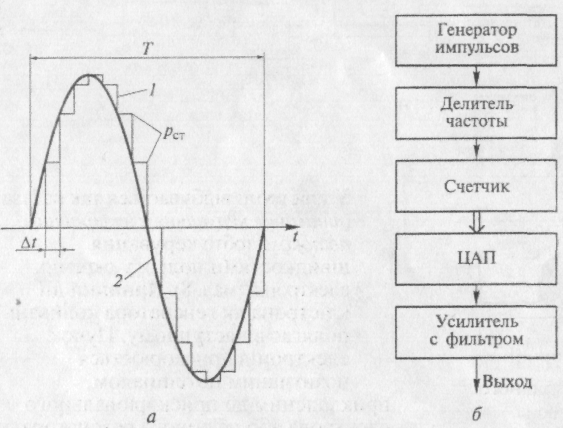
Рис. 8 Цифровий генератор низьких частот:

а — східчаста апроксимація сигналів; б — спрощена структурна схема; 1 — східчаста (апроксимована) крива; 2 — апроксиміруєма крива (синусоїда).

а бо, з урахуванням значення ρ і співвідношення ω=2π/Τ записати як:

Крім того, східчаста крива тим точніше наближається за формою до синусоїди (зменшується погрішність апроксимації), чим більше обране число сходів р.

Коли це число досить велике, сформовану східчасту напругу можна розглядати як низькочастотну синусоїдальну напругу, перекручену в невеликому ступені високочастотною адитивною перешкодою.

Спектральний аналіз напруги, отриманої шляхом східчастої апроксимації, виявляє, що її спектр містить гармоніку основної частоти. Розкладання в ряд Фур'є показує, що найближчою вищою гармонікою буде складова (р -1), наступною гармонікою стане (р + 1), потім — гармоніки (2р - 1) й (2р + 1) і т.д. Наприклад, при р-25 і частоті напруги f основної гармоніки найближчими вищими гармоніками будуть 24, 26 й 49 й 51 -я гармоніки, тобто напруги частот 24f, 26f, 49 f і 51 f.

Такі співвідношення між основною і вищою гармоніками дозволяють просто здійснити високоякісну фільтрацію, різко послабляючи вищі гармоніки, тобто одержати синусоїдальну напругу, яка характеризується дуже малим коефіцієнтом нелінійних перекручувань (коефіцієнтом гармонік).

Спрощена структурна схема цифрового генератора, що формує східчасту криву, наведена на мал. 8, б. Імпульсний кварцовий генератор виробляє періодичну послідовність коротких імпульсів з періодом проходження Т. На виході дільника частоти з регульованим коефіцієнтом розподілу g виходить послідовність імпульсів з періодом проходження Δt = gT, що задає крок дискретизації.

Імпульси надходять у лічильник ємністю р. Кодова комбінація, обумовлена числом i імпульсів, накопичених у лічильнику, передається в схему ЦАП. Останній виробляє напругу, що відповідає числу і, тобто и(iΔt) = Umax sіп(і2π/р). У такий спосіб формуються сходи апроксимуючої кривої рст. Після нагромадження р імпульсів лічильник переповняється й скидається в нуль. Із приходом (р + 1)-го імпульсу починається формування нового періоду східчастої кривої.

Частоту формованого коливання при фіксованому числі сходів рст„ регулюють, змінюючи крок дискретизації Δt, що досягається шляхом зміни коефіцієнта розподілу g дільника частоти.