2 Використання генераторів синусоїдалного сигналу

Формування синусоїдних сигналів у цифрових генераторах ґрунтується на кусково-східчастій апроксимації. Залежно від того, рівномірно чи нерівномірно розташовані вузли апроксимації в часі і за рівнем, можливі три варіанти формування кусково-східчастого синусоїдного сигналу (на рис. 5 показаний півперіод сигналу): з рівномірним розташуванням вузлів апроксимації в часі (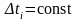 , а 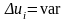), з рівномірним розташуванням вузлів апроксимації за рівнем (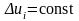 , а ), з оптимальним (нерівномірним) розташуванням вузлів апроксимації і в часі, і за рівнем (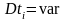 , ). В останньому випадку забезпечується мінімальне значення коефіцієнта гармонік і найкраще наближення сформованого сигналу до синусоїди 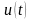при заданому числі рівнів апроксимації.

Ефективність варіантів методу кусково-східчастої апроксимації визначається двома основними показниками: ступенем наближення кривої сформованого сигналу до синусоїди і складністю апаратурної реалізації.

Ступінь наближення форми сигналу до синусоїди задається його спектральним складом або коефіцієнтом гармонік. Для визначення спектрального складу використовують розклад сигналу в ряд Фур'є, який показує, що кусково-східчастий сигнал містить, крім основної, вищі гармоніки порядку 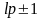, де p  число ділянок апроксимації (сходинок) за період сигналу; . Наприклад, при числі сходинок 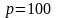в сигналі будуть присутніми 99, 101, 199, 201, 299, 301 і т.д. вищі гармоніки, причому їхні амплітуди різко убувають із зростанням номера гармоніки (приблизно обернено пропорційно номеру гармоніки). Таким чином, збільшення числа ділянок апроксимації обумовлює зменшення амплітуд і збільшення номерів вищих гармонік в кусково-східчастому сигналі. При необхідності вищі гармоніки можуть бути відфільтровані і тим самим покращена якість сигналу.

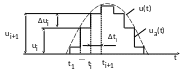
Рис. 4. До пояснення цифро аналогового формування сигналів.

Загальновживаною і найбільш розповсюдженою кількісною оцінкою ступеня відтворення синусоїдного сигналу є коефіцієнт гармонік. Для його визначення при великому числі сходинок p ( ) справедлива асимптотична формула

,

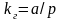де а  числовий коефіцієнт, який набирає конкретних значень для кожного з трьох варіантів кусково-східчастої апроксимації: для рівномірної за часом ач ; для рівномірної за рівнем ; для оптимальної . При великих значеннях p оптимальна апроксимація зменшує коефіцієнт гармонік у порівнянні з рівномірною апроксимацією за рівнем на 5%, а у порівнянні з рівномірною апроксимацією за часом  на 15%. При невеликих p ця відмінність досягає 30...50%. Рівномірна апроксимація за рівнем у порівнянні з рівномірною апроксимацією за часом дає виграш 10 %.

Усі цифрові генератори з кусково-східчастою апроксимацією, незалежно від її виду, можна зобразити узагальненою схемою (рис. 2).

Генератор імпульсів є мірою часових інтервалів , при накопиченні яких формуються моменти дискретизації кусково-східчастого сигналу . Цю функцію виконує блок завдання моментів апроксимації , він формує, залежно від виду апроксимації, рівномірну або нерівномірну послідовність імпульсів, які потрапляють на вхід реверсивного лічильника. Код поточного числа імпульсів, записаного в реверсивному лічильнику, подається на кодові входи ЦАП і на його виході виникає кусково-східчаста напруга. Значення рівнів цієї напруги задаються реверсивним лічильником і визначаються законом зміни опорів у ЦАП.

Залежно від виду апроксимації ЦАП виконується або функціональним, або лінійним. Опір резисторів ЦАП підібраний так, що напруга на його виході змінюється за тими самими законами. Функціональний ЦАП використовується при рівномірній апроксимації за часом і оптимальній апроксимації. Лінійний ЦАП використовується при рівномірній апроксимації за рівнем, при цьому опори ЦАП і сходинки напруги на його виходах змінюються рівномірно. Функціональний (нелінійний) ЦАП може бути замінений лінійним, якщо між реверсивним лічильником і ЦАП увімкнути ПЗП, в який записати коди миттєвих значень сигналу, розраховані при проектуванні генератора. Оскільки синусоїдна функція симетрична, то її можна формувати або за чверть періоду або за півперіод з відповідним перемиканням режиму роботи реверсивного лічильника (підсумовування і віднімання) і режиму роботи ЦАП (полярність формованого сигналу). Для покращання якості вихідного сигналу між ЦАП і вихідним підсилювачем може вмикатися ФНЧ (він може входити до складу підсилювача), який заглушує вищі гармонічні складові у вихідному сигналі генератора.

Регулювання амплітуди вихідного сигналу цифрових генераторів здійснюється за допомогою подільника напруги або атенюатора, коефіцієнт передачі яких можна змінювати не тільки вручну, як у аналогових генераторів, але й автоматично за певною програмою.

Більш складним виявляється питання перебудови частоти f вихідного сигналу цифрових генераторів. Найпростіше воно вирішується при рівномірній апроксимації за часом. У таких генераторах функції блока завдання моментів дискретизації ti виконує подільник частоти, коефіцієнт ділення якого установлюється згідно зі співвідношенням . Звідси видно, що є дві технічні можливості перебудови частоти f вихідної напруги генератора. Одна з них полягає в регулюванні частоти генератора імпульсів, яке може здійснюватися плавно або дискретно, із заданим кроком. Саме такий принцип перебудови частоти знаходить застосування в сучасних цифрових генераторах. Його недоліком є невисока стабільність частоти вихідного сигналу, яка ідентична нестабільності генератора імпульсів. Тому в цифрових генераторах, прецизійних за частотою, доцільним є інший принцип її перебудови. Полягає він в одержанні високо стабільних коливань шляхом ділення частоти кварцового генератора подільником частоти зі змінним коефіцієнтом ділення. В цьому разі нестабільність частоти визначається дуже малою нестабільністю частоти кварцового генератора. Проте такий принцип перебудови частоти призводить до нелінійної залежності частоти f від змінного коефіцієнта ділення kд, що не дозволяє проградуювати частотну шкалу генератора безпосередньо в одиницях частоти. Цього недоліку можна позбутися, застосувавши мікропроцесор для лінеаризації шкали генератора.

Для розширення частотного діапазону сучасних цифрових генераторів, наприклад типу Г4-153, використовується кусково-східчастий метод формування сигналів спільно з двома іншими методами. Спрощена структурна схема таких генераторів наведена на рис.3. В цих генераторах кожному методу формування відповідає свій частотний канал і діапазон частот. У першому, високочастотному каналі синусоїдна напруга u(t) знімається безпосередньо з генератора, керованого напругою, частота якого перестроюється в діапазоні 1,0...11 МГц. У другому частотному каналі, який перекриває діапазон 0,1...1,0 МГц, синусоїдну напругу одержують виділенням основної гармоніки послідовності прямокутних імпульсів типу меандр, що формуються за допомогою подільника частоти 1 з коефіцієнтом ділення kд = 10, та блока фільтрів ФНЧ1.

Рис. 5. Узагальнена структурна схема цифрового генератора.

Рис. 6. Структурна схема цифрового генератора синусоїдної напруги.

Блок ФНЧ1 має п'ять фільтрів з різною смугою пропускання. Цифровий метод формування "синусоїдної" кусково-східчастої напруги реалізований у третьому частотному каналі з діапазоном частот від 10 Гц до 100 кГц. Під діапазони частот у цьому каналі задаються декадним змінюванням коефіцієнта ділення подільника частоти 2, а сигнал формується за допомогою ЦАП і одного з фільтрів блока ФНЧ2 з відповідною смугою пропускання. Частотні канали через керований аналоговий комутатор вмикаються до вихідного пристрою, в якому здійснюється регулювання амплітуди вихідної напруги за допомогою ЦАП. Перебудову частоти і амплітуди вихідної напруги можна виконувати органами керування, розміщеними на передній панелі, або дистанційно

Формування спеціальних сигналів (лінійно змінного, трикутного) і складних не синусоїдних сигналів проводиться за тим же методом  перетворювання заданих кодів миттєвих значень цих сигналів у кусково-східчастий сигнал за допомогою ЦАП.