§ 3.6. Оценивание результатов и погрешностей совокупных и совместных измерений с многократными наблюдениями

В § 1.2 отмечалось, что при совокупных и совместных измерениях искомые величины находят из решения системы уравнений (1.7), которая связывает их с величинами, непосредственно измеряемыми. При этом измерения осуществляются так, что получаемое число уравнений превышает число искомых переменных. Для этого про­водят многократные наблюдения одних и тех же физических вели­чин в одинаковых или различных условиях (в зависимости от кон­кретной задачи). Результаты наблюдений для всех измеряемых в каждом эксперименте величин могут быть обработаны методами, изложенными в § 3.4, 3.5, а затем их результаты могут быть сгруппированы в систему уравнений, из решения которой могут быть найдены m физических величин, определяемых совокупными или совместными измерениями. Оценка значений этих m величин и их погрешностей при этом можно найти так же, как и для косвенных измерений.

В настоящее время для обработки экспериментальных данных при выполнении совместных и совокупных измерений в большин­стве случаев применяют метод Лежандра, называемый методом наименьших квадратов.

Сущность этого метода состоит в следующем. Если в систему уравнений (1.7), записанную для краткости в виде

F_i(X₁,X₂,...,X_n, Y₁,Y₂,…,Y_m) = 0 (i=1,2,..., n), (3.28)

подставить значения величин Х₁, Х₂, ..., Х_n, полученных как резуль­таты наблюдений, то систему уравнений (3.28) можно преобразо­вать следующим образом:

F_i(Y₁ Y₂,..., Y_j,..., Y_m) = 0 (i=1,2..., n). (3.29)

Эта система содержит только искомые физические величины и по­стоянные коэффициенты. Число n равно общему числу наблюдений измеряемых величин Х_і (в том числе результаты повторных наблю­дений одной и той же величины). Из-за ограниченной точности из­мерений величин Х_і при числе наблюдений n, существенно большем числа неизвестных m, не представляется возможным найти такие значения неизвестных Y_j, при которых выполнялись бы все урав­нения полученной системы. Поэтому задача сводится к нахождению для искомых величин Y_J их оценок представляющих собой наи­лучшие приближения к истинным значениям. Уравнения (3.29) в отличие от обычных математических уравнений принято называть условными, так как подстановка в них найденных каким-либо пу­тем значений оценок не обращает уравнение в нуль:

F_i ( ) 0 (i = 1,2,..., n). (3.30)

Чтобы эти уравнения превратились в тождества, их следует за­писать в виде

F_i ( ) + υ_i = 0 (i = 1,2,...,n) . (3.31)

Величины υ_i принято называть невязками, или остаточными, по­грешностями уравнений.

Согласно методу наименьших квадратов, наилучшие оценки ве­личин могут быть найдены в том случае, если функция Ω, представляющая собой сумму квадратов остаточных погреш­ностей условных уравнений, будет минимальна:

Ω = = min. (3.32)

Суть метода наименьших квадратов может быть уяснена при рассмотрении определения параметров а и b линейной за­висимости ξ = aφ+b. Пусть в результате экспериментальных исследований найдены пары значений ξ_i и φ_i (рис. 3.3).

В соответствии с методом наименьших квадратов для прямой, наи­лучшим образом проходящей относительно всех n точек, получен­ных в результате экспериментальных исследований значения, а и b должны быть выбраны такими, чтобы функция Ω = была минимальна.

Рис. 3.3. График линейной зависимости, найденный методом наименьших квадратов

Рассмотрим теперь последовательность обработки эксперимен­тальных данных совокупных или совместных измерений для наиболее важного случая, когда в систему (1.7) входят только линей­ные независимые уравнения:

X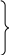 ₁ = k₁₁ Y₁ + k₁₂ Y₂ + … + k_1m Y_{m ,}

X₂ = k₂₁ Y₁ + k₂₂ Y₂ + … + k_2m Y_{m ,}

…………………………………… (3.33)

X_n = k_n1 Y₁ + k_n2 Y₂ + … + k_nm Y_{m ,}

где X_i (i=1, 2, ..., n) — результаты наблюдений измеряемых физи­ческих величин; k_ij — известные коэффициенты; Y_j (j==1, 2, ..., m)— искомые физические величины. Результаты наблюдений величины X_i — исправлены, равнорассеяны, некоррелированы и подчиняются нормальному закону распределения. Систему (3.33) можно запи­сать в виде

X_i = , (i = 1,2,..., n). (3.34)

Если коэффициенты k_ij в уравнениях (3.33) определены с такой малой погрешностью, что по сравнению с погрешностями измерений величин X_i ими можно пренебречь, то уравнение (3.33) считают точным.

Так как результаты наблюдений X_i содержат погрешность, то по аналогии с (3.31) для системы (3.34) запишем:

X_i= , (i=1,2,...,m). (3.35)

Для каждой остаточной погрешности

υ_i = X_i - . (3.36)

Тогда для суммы квадратов остаточных погрешностей имеем

Ω = = ( X_i - )² = min. (3.37)

Для определения , удовлетворяющих условию (3.37), находят все честные производные функции Ω по Y_j, приравнивают их к нулю и получают тем самым новую систему из m уравнений:

= -2 ( X_i - ) k_ij = 0 (j=1,2,...,m), (3.38)

или

( X_i - ) k_ij = 0 (j=1,2,...,m). (3.39)

Эта система является линейной относительно искомых величин . Ее называют системой нормальных уравнений. Число этих уравне­ний всегда равно числу неизвестных величин Y_j, Для упрощения написания системы нормальных уравнений пользуются обозначениями Гаусса для сумм:

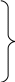= [k_j k_j],

k_ij k_il = [k_j k_l] (l=1,2,...,m), (3.40)

X_i = [k_jX].

Для рассматриваемого случая система нормальных уравнений имеет вид:

[ k₁k₁] + [k₁k₂] + … + [k₁k_m] = [k₁X],

[k₂k₁] + [k₂k₂] + … + [k₂k_m] = [k₂X],

……………………………………………. (3.41)

[k_mk₁] + [k_mk₂] + … + [k_mk_m] = [k_mX],

Решение системы (3.41) находят с помощью определителей для каждой из искомых величии:

= D_j/D, (3.42)

г де

[k₁k₁]…[k₁k_j]…[k₁k_m]

D = ···································

[k_mk₁]…[k_mk_j]…[k_mk_m]

[k₁k₁]…[k₁X]…[k₁k_m]

D_j = ···································

[k_mk₁]…[k_mX]…[k_mk_m]

Определитель D_j получен заменой в определителе D j-го столбца столбцом свободных членов (3.41).

Получение оценок искомых величин связано с большим объе­мом вычислений. Причем объем вычислений быстро увеличивается с увеличением числа условных уравнений. Последнее необходимо для увеличения точности получаемых оценок. В настоящее время обработка результатов совокупных и совместных измерений осу­ществляется с помощью электронных цифровых вычислительных машин, что позволяет использовать для получения оценок несколь­ко десятков или даже сотен условных уравнений.

Оценку среднеквадратического отклонения результата измере­ния величины Y_j определяют по формуле

, (3.43)

где D_jj — алгебраическое дополнение определителя D, получаемое путем удаления из него j-и строки и j-го столбца; S² -оценка дис­персии условных уравнений.

Для определения S² используют формулу

S² = ( X_i - )². (3.44)

Доверительные интервалы для истинных значений всех измеряе­мых величин получают на основе распределения Стьюдента при числе степеней свободы, равном n—m.

Если при совокупных или совместных измерениях условные уравнения нелинейны, то применяют их линеаризацию [9, 10].