§3.4. Оценивание результата и погрешности прямых измерений с многократными наблюдениями

Рассмотренные в § 1.4 характеристики случайной величины справедливы только при бесконечно большом числе наблюдений, т. е. они в сущности являются теоретическими. На практике число наблюдений, выполняемых при проведении измерительных экспериментов, ограничено и редко превосходит 20—30. Поэтому для обработки результатов измерительных экспериментов используют математическую статистику. В общем случае для выявления закономер­ностей, отражающих поведение случайной величины при ограниченном числе наблюдений, в математической статистике также решается задача определения закона распределения. Однако выявляемые при этом закономерности содержат элемент случайности. Статистический материал может только с большим или меньшим правдоподобием подтверждать или не подтверждать справедливость того или иного предположения (задача проверки правдоподобия гипотез). Чаще при обработке результатов наблюдений при измерении физических величин не возникает вопрос об определении закона распределения. Обычно это бывает связано с малым числом наблюдений (например, при 3—5 наблюдениях) или априорным утверждением о том, что закон распределения случайной величины является нормальным. Последнее утверждение, как показывает практика обработки результатов измерительных экспериментов, оказывается в подавляющем большинстве случаев оправданным. В этих случаях решается более узкая задача, состоящая в определении указанных числовых параметров М[Х] и σ. Поскольку на основе ограниченного статистического материала можно найти только приближенные значения М[Х] и σ, их называют оцен­ками параметров функции распределения случайной величины, а так как они выражаются одним числом, их называют также то­чечными оценками. Оценкой математического ожидания служит среднее арифметическое:

(3.3)

Для оценки среднеквадратического σ отклонения используется формула

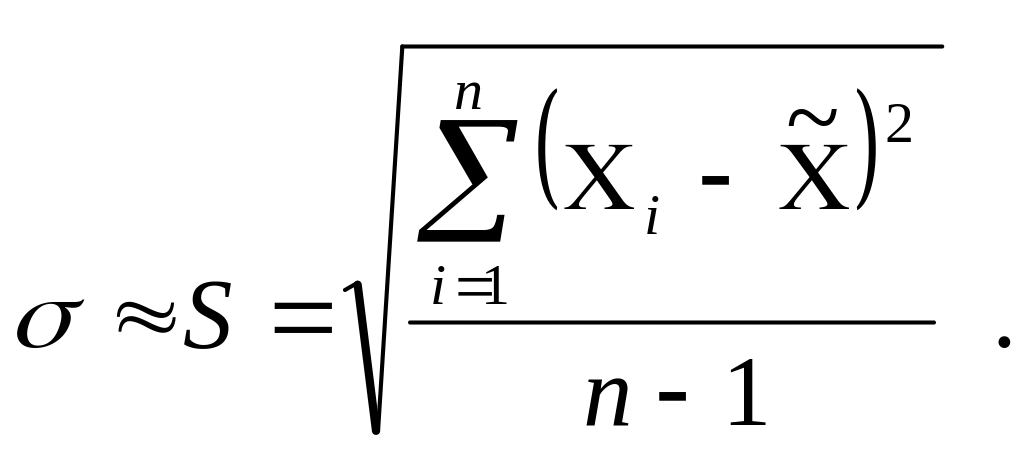(3.4)

Оценку S приписывают каждому из n результатов наблюдений и называют погрешностью единичного измерения, стандартным от­клонением или стандартом.

Таким образом, приведенные оценки являются случайными ве­личинами. Если провести повторное измерение и по результатам его наблюдений вычислить и S, то их значения будут отличаться от прежних. Повторяя измерения и вычисляя по результатам их на­блюдений и S или обрабатывая совместно наблюдения, получен­ные в предыдущих и последующих опытах, можно получить ряд значений и S, которые также подчиняются нормальному закону распределения. Для оценки рассеяния этих распределений исполь­зуют понятие среднеквадратического отклонения среднего арифме­тического, которое используют в качестве оценки среднеквадрати­ческого отклонения результата измерения и определяют по фор­муле

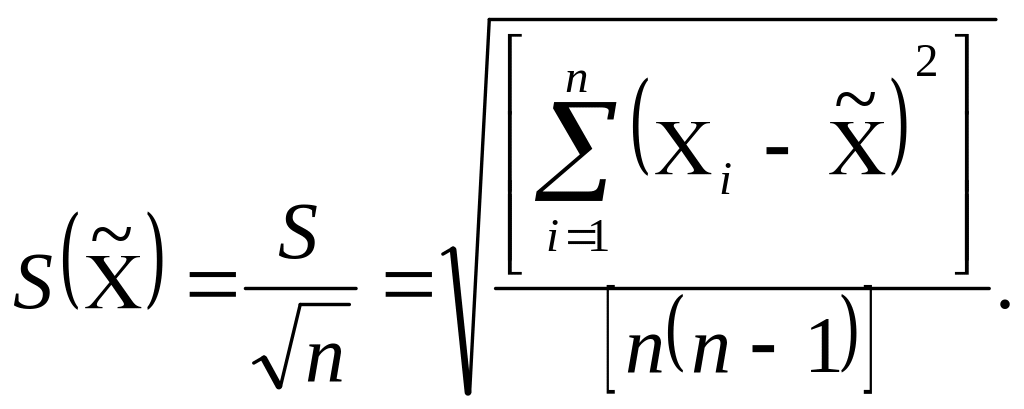(3.5)

Из формулы видно, что оценка среднего квадратического откло­нения результата измерения в раз меньше оценки среднеквад­ратического отклонения S результатов отдельных наблюдений.

Приведенные точечные оценки S, S и рассмотренные поня­тия доверительного интервала и доверительной вероятности исполь­зуются для определения интервальной оценки погрешности резуль­тата измерения. Причем для определения доверительного интер­вала при принятом или заданном значении доверительной вероят­ности Р_д вместо нормального распределения, которое описывает поведение случайных величин при бесконечно большом числе на­блюдений, используют распределение Стьюдента, или t-pacпределение (предложено английским статистиком Госсетом, публико­вавшимся под псевдонимом «студент»), которое обеспечивает возможность определения доверительных интервалов при ограничен­ном числе измерений. Границы доверительного интервала при этом определяются по формуле

(3,6)

где t — коэффициент распределения Стьюдента, зависящий от зада­ваемой доверительной вероятности Р_д и числа наблюдений n. Коэф­фициент t определяют по таблице (приложение 2) или рассчитыва­ют по формуле, описывающей указанное распределение:

(3.7)

где —плотность распре­деления Стьюдента; k — вели­чина, называемая степенью свободы и равная n—1.

Коэффициент t определяет­ся дробью , которая называется дробью Стьюдента. При n (прак­тически при ) распреде­ление Стьюдента приближается к нормальному.

Получение n результатов наблюдений

Вычисление среднего арифметического по формуле (3.3)

Вычисление оценки среднеквадратического отклонения одиночного наблюдения по формуле (3.4)

Вычисление оценки среднеквадратического отклонения результата измерения по формуле (3.5)

Принятие значения доверительной вероятности (обычно Р_Д = 0,95)

Определение коэффициента t в зависимости от Р_Д и n по таблице распределения Стьюдента

Определение доверительных границ ψ_Д случайной погрешности по формуле (3.6)

Запись результата измерения с использованием правил округления в виде:

Рис. 3.1. Последовательность обработки экспериментальных данных прямых из­мерений с многократными наблюдениями

Как отмечалось в § 1.4, слу­чайные погрешности, не свя­занные с действиями операто­ра, проводящего измерение, подразделяют на ожидаемые и грубые. Если в процессе изме­рений оператор обнаруживает, что результат одного или не­скольких наблюдений резко отличается от остальных и оп­ределяет причину этого, то он должен отбросить этот резуль­тат (или результаты) и прове­сти дополнительные наблюде­ния. Когда осуществляется об­работка уже имеющегося мате­риала и нет возможности учесть все условия, при кото­рых выполнялся измеритель­ный эксперимент, обнаружение грубых погрешностей осуществляется методами проверки статисти­ческих гипотез. Основная концепция этих методов состоит в том, что проверяется гипотеза, утверждающая, что результат i-го на­блюдения Х_і не содержит грубой погрешности, т. е. является одним из значений случайной величины X с законом распределения Р(X) (обычно нормальным), оценки параметров которого и S предва­рительно определены.

Для обнаружения в соответствии с этими методами грубых по­грешностей используется ряд критериев (критерий Зσ, Шовине, Ро­мановского, Гребса) [9, 10].

Последовательность обработки экспериментальных данных для наиболее простого и типичного случая приведена на рис. 3.1. В данном случае предполагается, что наблюдения, получаемые при измерении, являются равнорассеянными (равноточными), т. е. пред­ставляют собой независимые, одинаково распределенные величины (такие результаты наблюдений получаются при выполнении изме­рений одним оператором с помощью одних и тех же средств изме­рений); результаты наблюдений являются исправленными, т. е. из них исключены систематические погрешности; неисключенные си­стематические погрешности настолько малы, что ими можно прене­бречь; из результатов наблюдений исключены промахи и грубые погрешности; число наблюдений не превосходит 15 (в этом случае признается и не проверяется их принадлежность нормальному рас­пределению).

На рис. 3.1 в п. 8 вместо доверительных границ случайной по­грешности ψ_Д записана суммарная погрешность измерения Δ [см. (1.8) ], так как в рассматриваемом случае систематическая по­грешность θ исключена, а неисключенная систематическая по­грешность, описываемая выражением (3.2), мала. Если исключен­ной систематической погрешностью нельзя пренебречь, то общую погрешность измерения вычисляют по формуле [28]

(3.8)

где — коэффициент, зависящий от случайной и неисключенной систематической погрешности; — оценка суммарного среднеквад-ратического отклонения результата измерения. Значения S2 и х вычисляют по формулам:

(3.9)

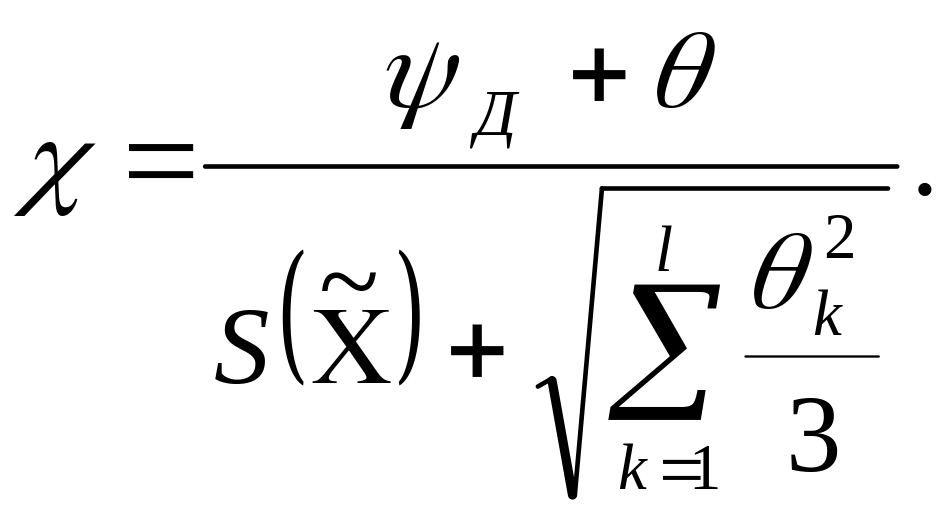(3.10)