
- •Глава 2
- •§ 2.1. Классификация средств измерений
- •§ 2.2. Структурные схемы измерительных устройств.
- •§ 2.3. Статические характеристики и параметры измерительных устройств
- •§ 2.4. Динамические характеристики измерительных устройств
- •§ 2.5, Погрешности измерительных устройств
- •§ 2.6. Нормирование метрологических характеристик измерительных устройств
- •§ 2.7. Структурные схемы и метрологические характеристики измерительных систем
- •§ 2.8. Надежность средств измерений
- •§ 2,9. Сведения о средствах измерений государственной системы промышленных приборов и средств автоматизации
§ 2.5, Погрешности измерительных устройств
Инструментальная (см. рис. 1.7) погрешность (или погрешность измерительных устройств) имеет определяющее значение для наиболее распространенных технических измерений.
На рис. 2.6 приведена классификация погрешностей измерительных устройств по ряду признаков.
По характеру проявления при повторных измерениях одного и того же значения физической величины принято выделять систематическую и случайную погрешности (или составляющие погрешности) измерительных устройств. В эти понятия в основном вкладывается тот же смысл, что и в понятия систематической и случайной погрешностей измерений (см. § 1.4). Особенность здесь состоит в том, что всякое измерительное устройство предназначается для внесения определенности в исследуемый процесс, а наличие случайной составляющей погрешности приводит к неоднозначности. В связи с этим первая задача, которая обычно решается при создании измерительных устройств, состоит в том, чтобы случайную погрешность сделать незначительной. Если это условие выполняется, а элементы, входящие в состав измерительного устройства, стабильны, можно путем градуировки (см. гл. 15) обеспечить достаточно малые систематические погрешности измерительного устройства. Рассмотренная концепция используется как основная при создании рабочих средств измерений и, в частности, измерительных устройств для технологических измерений.
В зависимости от условий применения измерительных устройств различают основную и дополнительную погрешности (см. рис. 2.6).
Основной погрешностью средства измерений называют погрешность при использовании его в нормальных условиях. Нормальными условиями применения средств измерений называют условия, при которых влияющие величины имеют номинальные значения или находятся в пределах нормальной области значений. Нормальные условия применения указываются в стандартах или технических условиях на средства измерений. При использовании средств измерений в нормальных условиях считают, что влияющие на них величины практически никак не изменяют их характеристики.
Дополнительной погрешностью измерительного преобразователя (или изменением показаний измерительного прибора) называют изменение его погрешности, вызванной отклонением одной из влияющих величин от ее нормативного значения или выходом ее за пределы нормальной области значений. Дополнительная погрешность может быть вызвана изменением сразу нескольких влияющих величин.
Изменение погрешности, как и других характеристик и параметров измерительных устройств под действием влияющих величин, описывается функциями влияния (см. приложение 1).
Иными словами, дополнительная погрешность — это часть погрешности, которая добавляется (имеется в виду алгебраическое сложение) к основной в случаях, когда измерительное устройство применяется в рабочих условиях. Рабочие условия обычно таковы, что изменения значений влияющих величин для них существенно больше, чем для нормальных условий, т. е. область рабочих (часть этой области называют расширенной областью) условий включает в себя область нормальных условий.
В некоторых случаях основная погрешность измерительных устройств определяется для рабочей области изменения значений влияющих величин. В этих случаях понятие дополнительной погрешности теряет смысл.
В зависимости от режима применения различают статическую и динамическую погрешности измерительных устройств (см. приложение 1).
По форме представления принято различать абсолютную, относительную и приведенную погрешности измерительных устройств (рис. 2.6). Для измерительных приборов и преобразователей определение этих погрешностей специфично. У измерительных приборов имеется шкала, отградуированная в единицах входной величины, либо шкала, отградуированная в условных единицах с известным множителем шкалы, поэтому результат измерения представляется в единицах входной величины. Это обусловливает простоту определения погрешности измерительных приборов.
Абсолютной погрешностью измерительного прибора Δ называют разность показаний прибора Хп и истинного (действительного) Хд значения измеряемой величины:
Δ = Хп-Хд. (2.11) Действительное значение определяется с помощью образцового прибора или воспроизводится мерой.
Относительной погрешностью измерительного прибора называют отношение абсолютной погрешности измерительного прибора к действительному значению измеряемой величины. Относительную погрешность выражают в процентах:
δ = Δ100/Хд. (2.12)
Так как Δ<<Хд или Хп, то в выражении (2.12) вместо значения Хд может быть использовано значение Хп.
Приведенной погрешностью измерительного прибора называют отношение абсолютной погрешности измерительного прибора к нормирующему значению XN- Приведенную погрешность также выражают в процентах:
γ =Δ100/ХN (2.13)
Гистерезиса
Линейности

Мультипликативная


Аддитивная
приведенная
Относительная
Абсолютная


Динамическая
Статическая

Дополнительная
Основная

Рис.2.6 классификация
п
Случайная
и змерительных
устройств
Систематическая
В качестве нормирующего значения используется верхний предел измерений, диапазон измерений и др., т. е.
γ = Δ 100/(XB-XH)
У измерительных преобразователей результаты измерений представляются в единицах выходной величины. В связи с этим для измерительных преобразователей принято различать погрешности по входу и выходу. При определении этих погрешностей необходимо знать приписанную данному измерительному преобразователю функцию преобразования (градуировочную характеристику) Y=f(X)
Абсолютной погрешностью измерительного преобразователя по выходу Δу называют разность между действительным значением величины Yп на выходе преобразователя, отображающей измеряемую величину, и значением Yд величины на выходе, определяемым по действительному значению величины на входе с помощью градуировочной характеристики, приписанной преобразователю:
ΔУ = YП-YД, (2.15)
где YП — значение выходного сигнала преобразователя при определенном значении входного сигнала; YД — значение выходного сигнала, который должен вырабатываться преобразователем, лишенным погрешности, при том же значении входного сигнала. Значение YП определяют с помощью образцового средства измерений, а значение YД рассчитывают с помощью функции преобразования по действительному значению входной величины ХД, которое воспроизводится мерой или определяется с помощью соответствующего образцового средства измерений:
YД = ƒ(ХД). (2.16)
Из (2.15) и (2.16) находим
ΔУ=YП-ƒ (ХД). (2.17)
Абсолютной погрешностью измерительного преобразователя по входу ΔХ называют разность между значением ХП величины на входе преобразователя, определяемым по действительному значению YД величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и действительным значением ХД величины на входе преобразователя:
ΔХ=ХП-ХД. (2.18)
Значение ХД определяется с помощью соответствующего образцового средства измерений или воспроизводится мерой, а значение ХП определяется по значению YП выходного сигнала с помощью функции преобразования, решенной относительно X, т. е. ХП = φ(YП) (φ — символ обратный функции преобразования). Таким образом,
ΔХ= φ(YП) - ХД. (2.19)
Относительной погрешностью измерительного преобразователя по входу (выходу) называют отношение абсолютной погрешности измерительного преобразователя по входу (выходу) к действительному значению величины на входе (к значению величины на выходе, определяемому по действительному значению величины на входе по градуировочной характеристике, приписанной преобразователю) :
![]() (2.20)
(2.20)
 ,
(2.21)
,
(2.21)
где
![]() Х
и
Y
— относительная погрешность по входу
и выходу соответственно.
Х
и
Y
— относительная погрешность по входу
и выходу соответственно.
Приведенной погрешностью измерительного преобразователя по входу (выходу) называют отношение абсолютной погрешности к нормирующему значению входного ХN (выходного YN) сигнала:
![]() (2.22)
(2.22)
![]() (2.23)
(2.23)
где γХ и γY — приведенная погрешность измерительного преобразователя по входу и выходу соответственно.
Обычно в качестве нормирующего значения используется диапазон измерении преобразователя ХВ — XН или соответствующий ему диапазон измерений выходного сигнала YB—YH. Тогда
![]() (2.24)
(2.24)
![]() (2.25)
(2.25)
Для измерительных преобразователей с линейной функцией преобразования вида Y — YH = K(X — ХН) приведенные погрешности по входу и выходу в соответствии с (2.24) и (2.25) определяются выражениями:
![]() (2.26)
(2.26)
![]() (2.27)
(2.27)
где К — коэффициент преобразования измерительного преобразователя, определяемый отношением (YВ—YН)/(ХВ — ХН).
Чрезвычайно важным для применения измерительных устройств и правильной оценки погрешности измерений, получаемой при их использовании, являются сведения о зависимости погрешности от значения измеряемой величины в пределах диапазона измерений, а также сведения о изменениях этой погрешности под действием влияющих величин.
Зависимость погрешности от значения измеряемой величины определяется принятой конструкцией (схемой) и технологией изготовления измерительного устройства. Влияние названных факторов на эту зависимость различно. Зависимость погрешности от значения измеряемой величины свойственна всем измерительным устройствам данного типоразмера, построенным по принятой конструкции. Влияние технологии изготовления на рассматриваемую зависимость индивидуально для каждого экземпляра, т. е. значения погрешностей при одних и тех же значениях измеряемого параметра различны для различных экземпляров измерительного устройства данного типоразмера.
Для рассмотрения зависимости погрешности измерительных устройств от значения измеряемой величины удобно использовать понятие номинальной и реальной функций преобразования измерительного устройства.
Номинальной (или идеальной) функцией преобразования называют функцию преобразования, которая приписана измерительному устройству данного типа, указана в его паспорте и используется при выполнении с его помощью измерений.
Реальной функцией преобразования называют ту функцию преобразования, которой обладает конкретный экземпляр измерительного устройства данного типа.
Из-за несовершенства конструкции и технологии изготовления реальная функция преобразования измерительного устройства отличается от номинальной. Это отличие и определяет погрешность данного измерительного устройства. Отклонения реальной характеристики от номинальной различны и зависят от значения измеряемой величины. По этому признаку погрешности принято разделять (рис. 2.6) на аддитивную, мультипликативную, линейности и гистерезиса.
Графически образование перечисленных погрешностей показано на рис. 2.7,
Аддитивной (получаемой путем сложения), или погрешностью нуля измерительных устройств, называют погрешность, которая остается постоянной при всех значениях измеряемой величины.
Р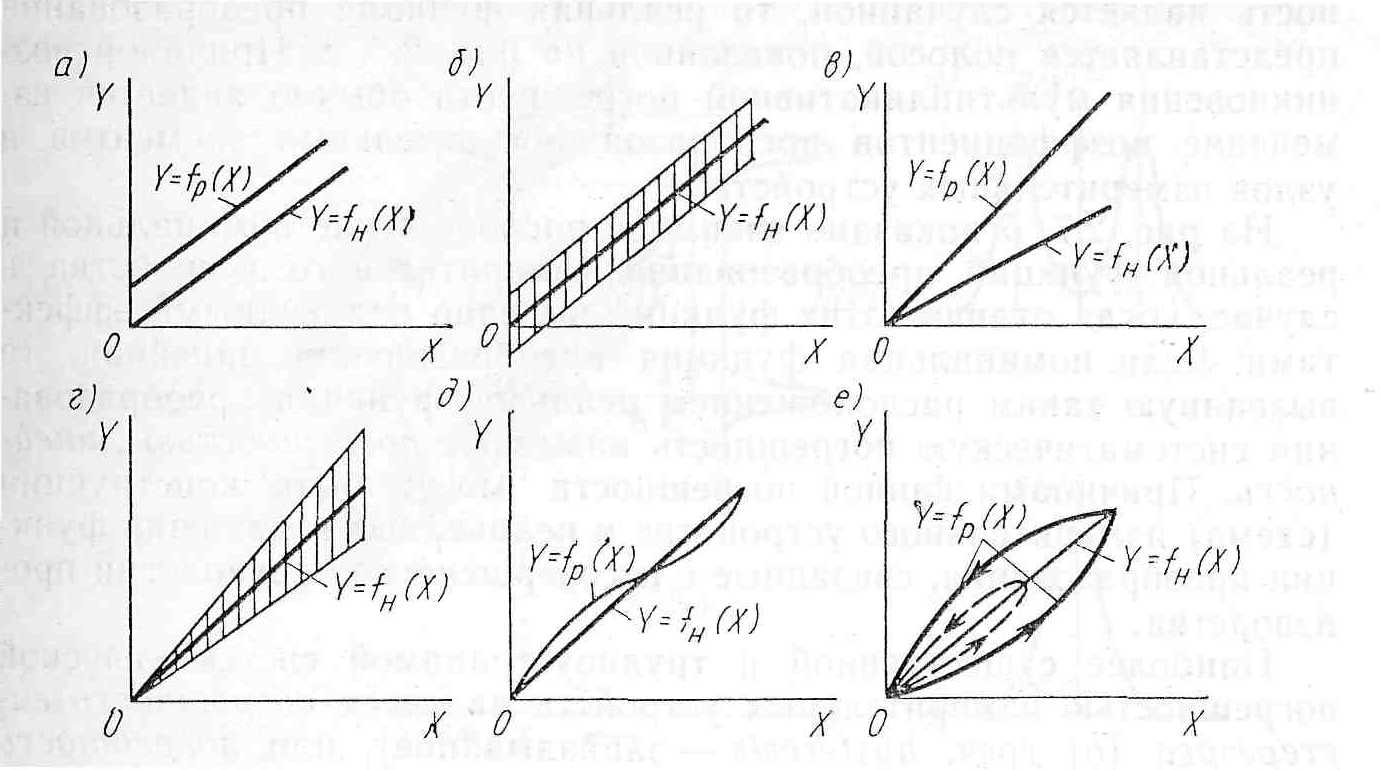 ис.
2.7. Реальные функции преобразования
измерительных устройств
ис.
2.7. Реальные функции преобразования
измерительных устройств
На рис. 2.7, а показано, что реальная функция преобразования Y=fp(X) несколько смещена относительно номинальной Y—fH(X), т. е. выходной сигнал измерительного устройства при всех значениях измеряемой величины X будет больше (или меньше) на одну и ту же величину, чем он должен быть, в соответствии с номинальной функцией преобразования.
Если аддитивная погрешность является систематической, то она может быть устранена. Для этого в измерительных устройствах обычно имеется специальный настроечный узел (корректор) нулевого значения выходного сигнала.
Если аддитивная погрешность является случайной, то ее нельзя исключить, а реальная функция преобразования смещается по отношению к номинальной во времени произвольным образом. При этом для реальной функции преобразования можно определить некоторую полосу (рис. 2.7, б), ширина которой остается постоянной при всех значениях измеряемой величины.
Возникновение случайной аддитивной погрешности обычно вызвано трением в опорах, контактными сопротивлениями, дрейфом нуля, шумом и фоном измерительного устройства (см. приложение 1).
Мультипликативной (получаемой путем умножения), или погрешностью чувствительности измерительных устройств, называют
погрешность, которая линейно возрастает (или убывает) с увеличением измеряемой величины.
Графически появление мультипликативной погрешности интерпретируется поворотом реальной функции преобразования относительно номинальной (рис. 2.7, в). Если мультипликативная погрешность является случайной, то реальная функция преобразования представляется полосой, показанной на рис. 2.7, г. Причиной возникновения мультипликативной погрешности обычно является изменение коэффициентов преобразования отдельных элементов и узлов измерительных устройств.
На рис. 2.7, д показано взаимное расположение номинальной и реальной функций преобразования измерительного устройства в случае, когда отличие этих функций вызвано нелинейными эффектами. Если номинальная функция преобразования линейная, то вызванную таким расположением реальной функции преобразования систематическую погрешность называют погрешностью линейности. Причинами данной погрешности могут быть конструкция (схема) измерительного устройства и нелинейные искажения функции преобразования, связанные с несовершенством технологии производства.
Наиболее существенной и трудноустранимой систематической погрешностью измерительных устройств является погрешность гистерезиса (от греч. hysteresis — запаздывание), или погрешность обратного хода, выражающаяся в несовпадении реальной функции преобразования измерительного устройства при увеличении (прямой ход) и уменьшении (обратный ход) измеряемой величины (рис. 2.7, е). Причинами гистерезиса являются: люфт и сухое трение в механических передающих элементах, гистерезисный эффект в ферромагнитных материалах, внутреннее трение в материалах пружин, явление упругого последействия в упругих чувствительных элементах, явление поляризации в электрических, пьезоэлектрических и электрохимических элементах и др. Существенным при этом является тот факт, что форма получаемой петли реальной функции преобразования зависит от предыстории, а именно от значения измеряемой величины, при котором после постепенного увеличения последней начинается ее уменьшение (на рис. 2.7, е это показано пунктирными линиями).
Для количественной оценки погрешности гистерезиса обратимся к рис. 2.8. Здесь показан фрагмент взаимного расположения реальной и номинальной функций преобразования измерительного устройства, обладающего погрешностью гистерезиса. Под действием влияющих величин реальная функция преобразования изменяет свое расположение и форму. На рис. 2.8, а для примера показаны два ее расположения, нанесенные сплошной и пунктирной линиями. При нормальных условиях эксплуатации измерительного устройства все изменения формы реальной функции преобразования не выходят за пределы заштрихованных на рис. 2.8, а полос- как для верхней, так и для нижней ее ветвей. Если влияющие величины, вызывающие изменения положения и формы функции преобразования, при измерении не выявляются, то рассматриваемое явление определяется как невоспроизводимость и характеризует случайную погрешность измерительного устройства. При этом используют понятие «размах» и «вариация».
Р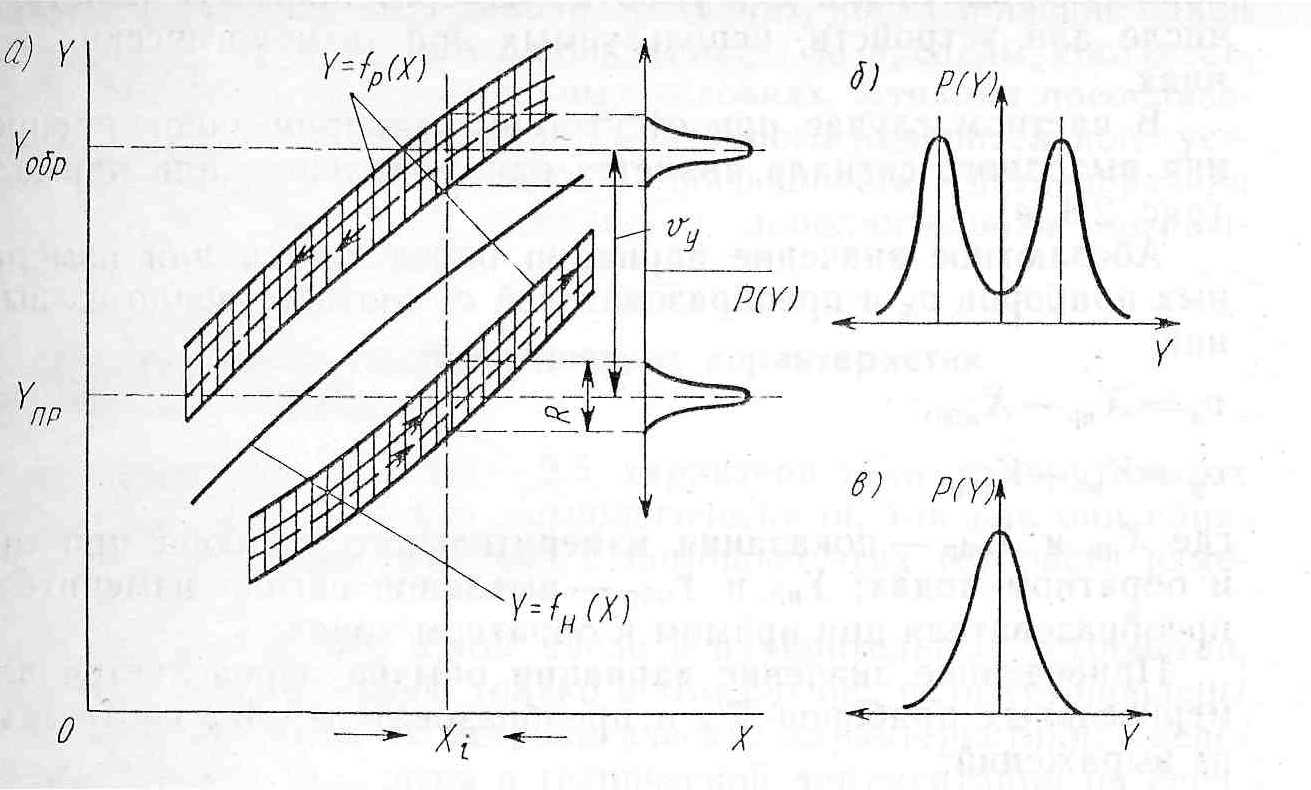 ис.
2.8. Взаимное расположение реальной и
номинальной функций преобразования
измерительного устройства, обладающего
погрешностью гистерезиса
ис.
2.8. Взаимное расположение реальной и
номинальной функций преобразования
измерительного устройства, обладающего
погрешностью гистерезиса
Размахом, (непостоянством) R выходного сигнала измерительного преобразователя (показаний измерительного прибора) называют разность между наибольшим и наименьшим значениями выходного сигнала, соответствующими одному и тому же значению измеряемой величины и полученными при многократном и одностороннем подходе к этому значению, т. е. при постепенном увеличении или уменьшении измеряемой величины (только при прямом или только при обратном ходе).
Размах характеризует ширину заштрихованных на рис. 2.8, а полос, определяющих случайную погрешность при значении измеряемого параметра, равном Xi.
Вариацией υY выходного сигнала измерительного преобразователя (показаний измерительного прибора) называют среднюю разность между значениями выходного сигнала, соответствующими одному и тому же значению измеряемой величины, полученными при многократном и двустороннем подходе к этому значению, т. е. при постепенном увеличении и последующем уменьшении измеряемой величины (иначе говоря, при прямом и обратном ходе).
Как видно из рис. 2.8, а, при одном и том же значении измеряемой величины Xi закон распределения выходного сигнала измерительного устройства при наличии вариации является двухмодальным. Если размахи для нижней и верхней ветвей функции преобразования перекрываются, то закон распределения выходного сигнала имеет вид, показанный на рис. 2.8, б. Формы функций преобразования с законами распределения (рис. 2.8, а, б) являются наиболее типичными для рабочих измерительных устройств, в том числе для устройств, используемых при технологических измерениях.
В частном случае при отсутствии вариации закон распределения выходного сигнала является одномодальным или нормальным (рис. 2.8, б).
Абсолютное значение вариации определяется для измерительных приборов υX и преобразователей υY соответственно из выражений:
υX = Xпр –Xобр, (2.28)
υY = Yпр-Yобр (2.29)
где Хпр и Хобр — показания измерительного прибора при прямом и обратном ходах; Yпр и Y0бР — выходной сигнал измерительного преобразователя при прямом и обратном ходах.
Приведенное значение вариации обычно определяется для измерительных приборов WХ и преобразователей WY соответственно из выражений:
![]() (2.30)
(2.30)
![]() (2.31)
(2.31)
т. е. определяется как отношение абсолютного значения вариации к диапазону измерения по входу или по выходу измерительного устройства.
и |
Использование
приведенных представлений о номинальной
и реальной функциях преобразования
позволяет наглядно отразить изменения
погрешностей измерительных устройств
под действием влияющих величин (рис.
2.9). Предположим, что при эксплуатации
некоторого измерительного устройства
в нормальных условиях его реальная
функция преобразования имеет вид
петлеобразной кривой 1, где заштрихованная
полоса определяет случайную погрешность,
вызванную изменением влияющих величин
в допустимых нормальными условиями
пределах. При этом обычно для
измерительного устройства устанавливается
значение огновной
погрешности.
На рис. 2.9
это показано графически в виде полосы
шириной
![]() .
Если измерительное устройство
эксплуатируется в рабочих условиях,
когда значение одной или нескольких
влияющих величии выходит за пределы,
соответствующие значениям при
нормальных условиях, функция преобразования
выходит за установленное для данною
измерительного устройства значение
полосы основной погрешности (петлеобразная
кривая 2 на рис. 2.9), т. с. появляется
дополнительная погрешность.
.
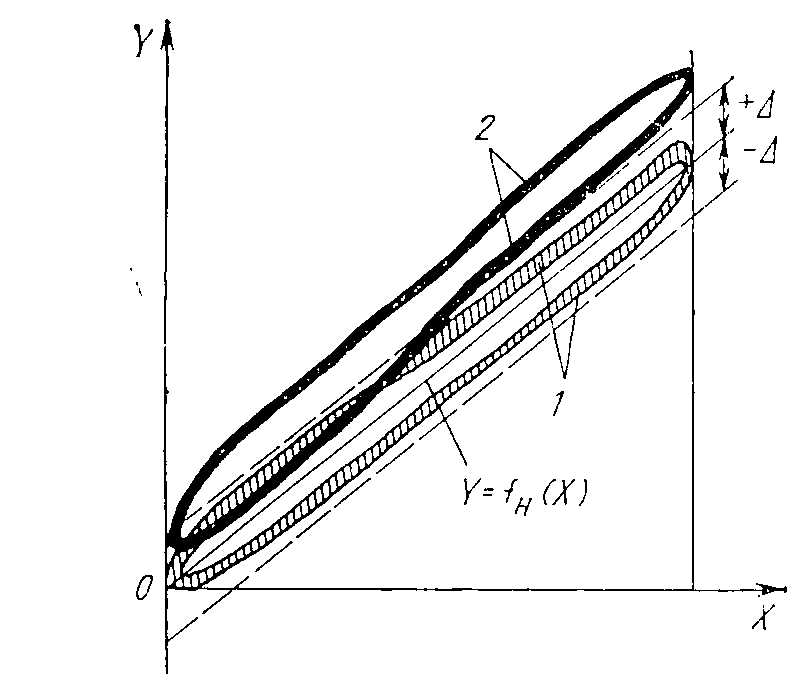
Если измерительное устройство
эксплуатируется в рабочих условиях,
когда значение одной или нескольких
влияющих величии выходит за пределы,
соответствующие значениям при
нормальных условиях, функция преобразования
выходит за установленное для данною
измерительного устройства значение
полосы основной погрешности (петлеобразная
кривая 2 на рис. 2.9), т. с. появляется
дополнительная погрешность.

 с.
2.9. Смещение реальной функции
преобразования при эксплуатации
измерительного устройства в рабочих
условиях
с.
2.9. Смещение реальной функции
преобразования при эксплуатации
измерительного устройства в рабочих
условиях