Тема 4. Прогнозирование временных рядов по трендовым моделям

1. Основные типы экономического роста и соответствующие им трендовые модели

Основные типы экономического роста:

1 тип – постоянный рост (одинаковые/почти одинаковые абсолютные цепные приросты). Моделируется с помощью линейных (близких к линейному) моделей;

2 тип – увеличивающийся рост (абсолютные цепные приросты увеличиваются)

3 тип – уменьшающийся рост (абсолютные цепные приросты уменьшаются)

4 тип – рост с качественными изменениями (изменения динамических характеристик на протяжении исследуемого периода).

Трендовые модели для каждого типа роста:

I тип роста

1. Линейная функция:

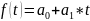
2. Линейно-гиперболическая функция

3. Линейно-логарифмическая функция второго порядка

II тип роста

2.1. Показательная функция

2.2. Парабола 2-го порядка

2.3. Парабола 3-го порядка

III тип роста

3.1. Степенная функция

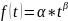
3.2. Линейно-логарифмическая функция

3.3. Парабола 2-го порядка

3.4. Гипербола 1-го порядка

3.5. Гипербола 2-го порядка

IV тип роста

1. Линейно-логарифмическая функция второго порядка

2. Парабола 3-го порядка

4.3. Логистическая функция

4.2. Первая функция Торнквиста

Введем замену:

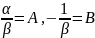
4.3. Кривая Гомперца

2. Оценивание параметров функции линейного тренда

Метод наименьших квадратов

На примере линейной функции

Доверительный интервал прогноза по линейному тренду:

–значения объясняющей переменной на прогнозный период

Получаемый таким образом доверительный интервал показывает верхнюю и нижнюю границы диапазона прогнозирования, вероятность попадания в который равна (1-α).

3. Оценивание параметров функций нелинейного тренда

Линеаризация:

1. замена переменной:

• полиномы m-го порядка. Пример

y = a₀+a₁*t+a₂*t² => t = Z₁, t² = Z₂

y = a₀+a₁*Z₁+a₂*Z₂

• гиперболические функции m-го порядка. Пример

y = a₀+a₁/t+a₂/t²=> 1/t = Z₁, 1/t² = Z₂

y = a₀+a₁*Z₁+a₂*Z₂

• линейно-логарифмическая функция m-го порядка. Пример

y = a₀+a₁*lnt+a₂*ln²t =>lnt = Z₁, ln²t = Z₂

y = a₀+a₁*Z₁+a₂*Z₂

• модифицированная экспонента.

f(t) = a₀ + a₁*e^btприb = -1 (Z=e^-t)

f(t) = a₀ + a₁*Z

• степенная функция

f(t) = α*t^β

lny = y, lnt = x(для регрессии) =>находим , =>подставляем f(t)=>прогноз

• показательная функция

2. специальные преобразования

Приближенные методы для расчета параметров кривых (IV тип роста)

Для функций вида:

y = a*b^t + k

метод трех сумм:

• весь ряд разбивается на 3 равных отрезка. Если количество элементов в ряду не кратно 3, то отбрасываются первые несколько наблюдений;

• для каждого отрезка вычисляется сумма элементов ряда (S₁,S₂,S₃);

• рассчитываются параметры;

• уточняем параметры.

Длявозрастающих рядов:S₁<S₂<S₃

Для убывающих рядов: S₁>S₂>S₃.Расчет параметров для логистической кривой:

Делим наш временной ряд на 3 равные части:

D₁ =S₁-S_2, D₂=S₂-S₃

α = k, β = b, γ = a

Кривая Гомперца (по методу 3-х сумм)

Уточнение параметров (метод Стонера)

Если левая часть меньше правой, то b нужно увеличить. Если левая часть больше правой, то bнужноуменьшить.

Первая функция Торнквиста

Вводятся следующие параметры: